|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| E. G. Phillips, M.A., M.Sc. — Functions of a complex variable with applications |
|
|
 |
| Предметный указатель |
Aerofoil 70
Algebra, the fundamental theorem of 113
Analytic continuation 103—107
Analytic function 105
Argand diagram 5
Argument 5
Argument, principle of the 108
Bilinear transformation see M bius bius
Biuniform mapping 33
Biuniform mapping by M bius' transformations 40 bius' transformations 40
Boundary point 8
Bounded set of points 8
Branch of function 20
Branch-point 28
Calculus of residues 114—137
Cardioid 02 77 81
Cauchy — Riemann equations 12 30 30 89
Cauchy’s integral 93
Cauchy’s residue theorem 115
Cauchy’s Theorem 89—92
Circle of convergence 17
Circular crescent 53 08
Circular sector, transformations of 09
Coaxal circles 40—48
Complex integration 85; see “Contour integral”
Complex numbers, abbreviated notation for 3
Complex numbers, argument of 5
Complex numbers, defined 1
Complex numbers, geometrical representation 5
Complex numbers, modulus of 2
Complex numbers, real and imaginary parts of 1
Confocal conics 71 74 81 82
Conformal transformations, definition of 32
Conformal transformations, tables of special 78 79
Conjugate, complex numbers 4
Conjugate, functions 14
Connex 9
Continuity 9
contour 80
Contour integral, definition of 88
Contour integration 117 128
Critical points oi transformations 37 45 55
Cross-cut 93
Cross-ratio 49
Curve, Jordan 8
Curve, Jordan curve theorem 9
Cut plane 27 59 70 73 120
De Moivre’s Theorem 6
Definite integrals, evaluation of 114—131
Determinant of transformation 41
Differentiability 10—11
Domain 9
Element of an analytic function 105
Elementary functions 17—25
ellipse 72 74
Equation, roots of 1 31 109 113
Equiangular spiral 31 82
Expansion, Laurent’s 97
Expansion, of function in a power series 18 95
Expansion, of meromorphic functions 131
Exponential function 20 31
Function, analytic 11 105
Function, holomorphic 11
Function, hyperbolic 23
Function, integral 21
Function, logarithmic 24
Function, manyvalued 20
Function, meromorphic 107 131
Function, rational 20 103
Function, regular 11
Gamma function 130
Goursat’s lemma 91
Green’s Theorem 89
Harmonic functions 37 111
Hyperbolic functions 23
Imaginary part 1
| Infinite integrals, evaluation of 119—130
Infinite integrals, principal value of 120
Infinity, point at 9 102
Integral functions 21
Interior point 8
Invariance of cross-ratio 49
inversion 43
Inversiontransformation 55
Isogonal transformation 32
Jordan curve 8
Jordan’s lemma 122
Laplace’s equation 15 30 54
Laurent expansion, theorem 97 112
Lima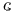 on 61 on 61
Limit point 8
Liouville’s theorem 90
Logarithm 21
Logarithmic function 24
M bius' transformations 40—56 bius' transformations 40—56
M bius' transformations, some special 51—54 bius' transformations, some special 51—54
Magnification 34 39 41
Many-valued functions 26
Mapping 32
Maximum modulus, principle of 109
Meromorphic function 107 131
Milne — Thomson’s construction 16
Modulus 2
Neighbourhood 7
One-one correspondence 33
parabola 62 64
Point at infinity 9 102
Poisson’s formula 111
Pole 99 107
Power series 17—25
Principal part at pole 99
Principal value, of  25 25
Principal value, of arg 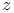 6 6
Principal value, of infinite integral 122
Principal value, of log 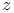 25 25
Radius of convergence of power series 17
Rational functions 20 103
Real part 1
Rectangular hyperbolas 61
Rectifiable curve 86
Regular function 11
Residue 99
Residue at infinity 114
Residue theorem 114
Riemann surface 27 59—60 63 71 73 75
Roots of equations 1 31 109 113
Rouch ’s theorem 108 ’s theorem 108
Schwarz — Christoffel transformation 80
Sets of points, bounded 8
Sets of points, closed and open 8
Sets of points, in Argand diagram 7—9
Singularity 11 99
Singularity of analytic function 105
Singularity, essential 99
Singularity, isolated 99
Singularity, nonisolated 101
Spiral, equiangular 31 82
Successive transformations 58 83
Summation of series 133 et seq.
Taylor’s series 101 112
Taylor’s Theorem 19 95—96
Term-by-term differentiation 19
Transformations, conformal 32 et seq.
Transformations, isogonal 32
Transformations, special 57—83
Transformations, tables of 78 79
Trigonometric functions 23
Uniform continuity 10 87
Upper bound for contour integral 88
Vectorial representation of complex numbers 6
Weierstrass' definition of analytic function 105
Zero 98 107
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 bius
bius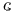 on
on 
 ’s theorem
’s theorem