|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bachman G. — Elements of Abstract Harmonic Analysis |
|
|
 |
| Предметный указатель |
 th power summable 1 th power summable 1
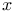 -section 177 -section 177
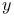 -section 177 -section 177
 -algebra 125 -algebra 125
Absolute continuity of a measure 245
Absolutely convergent trigonometric series, space of 26
Adherence point 62
Algebra,  -algebra 125 -algebra 125
Algebra, Banach 25
Algebra, completely symmetric Banach 210
Algebra, of sets 125
Algebra, with involution (star, symmetric) 97 188
Analytic vector-valued function 29
Approximate identity 9 190
Banach algebra 25
Banach space 2
Basis at a point 73
Basis of open sets 73
Bicontinuous mapping 62
Bochner’s theorem 223 246
Borel complex-measure 211
Borel measure 126
Borel regular-measure 215
Borel sets 125
Bounded linear functional 29
Canonical mapping 110
Cartesian product (of topological spaces) 78-79 85
Cauchy integral formula 32
Cauchy integral theorem 31
Cauchy — Hadamard formula 32
Cauchy — Schwarz inequality 17
CHARACTER 193 200
Closed set 62
Closure 62
Cluster point 123
Compact 81
Compact, locally 85
Compactification, one-point 118
Content 163
Content, inner 164
Content, regular 164
Continuity, uniform 107
Continuous mapping 62
Continuous partition of the identity 121
Convergence in a topological space 123
Convergence of a generalized sequence 116
Convolution 6 180
Coset 50
Countability, first axiom of 73
Countability, second axiom of 74
Countably additive class 125
Covering 81
Covering, finite 81
Covering, open 81
Daniell extension 158 166
Directed set 116
Discrete topology 61
Dominated Convergence Theorem 16
Double integral 178
Dual group 193
Duality theorem 241
Essential supremum (ess sup) 196
Extended Stone — Weierstrass Theorem 244
Extension theorem (Tietze) 118
Factor group 114
Fatou’s Lemma 16
Finite intersection property 83
Fourier Transform on 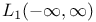 1 ff. 1 ff.
Fourier Transform on 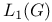 207 ff. 210 207 ff. 210
Fourier Transform on 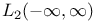 19-20 19-20
Fourier Transform on 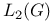 237 237
Fourier — Stieltjes transform 219 ff. 224
Fubini’s Theorem 16 179 213
Fundamental system of neighborhoods 74
Gel’fand theory 48 ff.
Gel’fand topology 87
Generalized Cauchy sequence 116
Generalized nilpotent element 57
Generalized sequence (convergence of) 116
Generated topology 77
Group, algebra 27
Group, dual 193
Group, factor 114
Group, general linear 99
Group, homogeneous 103
Group, quotient 114
Group, regular 106
Group, topological 98
Group, unimodular 99
H lder’s inequality 17 lder’s inequality 17
Haar covering function 130
Haar integral 128 129 172
Haar measure 126 169 172
Hausdorff space 80
Homeomorphism 62
Homogeneous 103
Ideal 48
Ideal, maximal 49
Ideal, principal 50
Ideal, proper 48
Identity, continuous partition of 121
Induced measure 128
Induced topology 78
Inner regular Borel measure; outer regular Borel measure 215
Interior point 71
Inversion formulas, 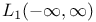 5 5
Inversion formulas, 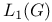 227 227
Inversion formulas, 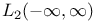 24 24
Involution, algebra with 97
Isomorphism 123
| Iterated integral 178
Jordan decomposition theorem 212
Lattice, linear vector 159
Lebesgue point 5
Limit point 123
Liouville’s theorem 30
Locally compact 85
Lower semicontinuous function 166
Maximal ideal 49
Measurable function 128
Measurable set 168
Measurable transformation 127-128
Measurable, 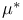 161 161
Measure, absolute continuity of 245
Measure, complex Borel 211
Measure, outer 64
Measure, product 176 ff.
Measure, signed 212
Minkowski inequality 17
Modular function 187
Natural mapping 110
Neighborhood 66 ff.
Neighborhood, fundamental system of 74
Neighborhood, symmetric 104
Neighborhood, topology 66 ff.
Nilpotent element 57
Normal space 117
Normal subgroup 110
Normed algebra 25
One-point compactification 118
Open mapping 111
Open sets 61
Open sets, in terms of neighborhoods 67
Outer measure 164
Parseval’s theorem 20 244
Plancherel’s theorem 24 235
Pontrjagin duality theorem 241
Positive definite function 220
Positive linear functional 158
Power set 61
Principal ideal 50
Product measures 176 ff.
Product space 78 79
Projection mapping 84
Proper ideal 48
Quotient algebra 50
Quotient group 114
Radical 56
Radon — Nikodym theorem 245
Regular content 163
Regular measure (inner, outer) 215
Regular point 37
Regular topological space 106
Relative topology 78
Representation theorem 160
Representation Theorem, Riesz 245
Resolvent operator 41
Riemann — Lebesgue lemma 4
Right Haar measure 126 172
Ring of sets 125
Semisimple 57
Separation axioms 79 ff.
Sigma$-bounded 164
Sigma$-ring 125
Simple function 217
Spectral radius 42
Spectrum of an element 37
Star (symmetric) algebra 97
Stone — Weierstrass theorem 244
Stronger topology 77
Subbasis (subbase) 75
Subgroup 109
Subgroup, closed 110
Subgroup, normal 114
Subspace topology 78
Summable set 168
Support of a function 107
Symmetric neighborhood 104
Tietze extension theorem 118
Tonelli — Hobson Theorem 17
Topological divisor of zero 53
Topological group 98
Topological group, homogeneous 103
Topological group, locally compact 107
Topological group, normal subgroup 114
Topological group, regular 106
Topological group, subgroup of 109
Topological space 61 ff.
topology 61
Topology, discrete 61
Topology, Gel’fand 87
Topology, generated 77
Topology, induced 78
Topology, relative (subspace) 78
Topology, trivial 61
Topology, Tychonoff 85
Topology, weak 78
Topology, weaker (stronger) 77
Total variation 211
Tychonoff theorem 85
Tychonoff topology 85
Uniformly continuous 107
Unimodular group 99
UNIT 34
Urysohn’s lemma 118
Weak topology 78
Weaker topology 77
Wiener theorem 60
Zero set 167
Zorn’s Lemma 49
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 th power summable
th power summable 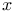 -section
-section 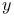 -section
-section  -algebra
-algebra 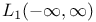
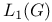
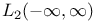
 lder’s inequality
lder’s inequality