During the past decade there has been an explosion in computation and information technology. With it has come vast amounts of data in a variety of fields such as medicine, biology, finance, and marketing. The challenge of understanding these data has led to the development of new tools in the field of statistics, and spawned new areas such as data mining, machine learning, and bioinformatics.
Many of these tools have common underpinnings but are often expressed with different terminology. This book descibes theimprtant ideas in these areas ina common conceptual framework. While the approach is statistical, the emphasis is on concepts rather than mathematics. Many examples are given, with a liberal use of color graphics. It should be a vluable resource for statisticians and anyone interested in data mining in science or industry.
The book's coverage is broad, from supervised learing (prediction) to unsupervised learning. The many topics include neural networks, support vector machines, classification trees and boosting — the first comprehensive treatment of this topic in any book.
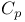Trevor Hastie, Robert Tibshirani, and Jerome Friedman are professors of statistics at Stanford University. They are prominent researchers in this area: Hastie and Tibshirani developed generalized additive models and wrote a popular book of that title. Hastie wrote much of the statistical modeling software in S-PLUS and invented principal curves and surfaces. Tibshirani proposed the Lasso and is co-author of the very successful An Introduction to the Bootstrap. Friedman is the co-inventor of many data-mining tools including CART, MARS, and projection pursuit.