|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Reid L.W. — The Elements of the Theory of Algebraic Numbers |
|
|
 |
| Предметный указатель |
0-function, expression for power of prime ideal 359
0-function, for ideals, definition 358
0-function, general expression 38 44 53 359-362 366 367
0-function, in k( ) 185-188 ) 185-188
0-function, in R, definition 37
0-function, of higher order 54 367
0-function, product theorem 45 360 361
0-function, summation theorem 46 75 362 363 367
Ambiguous ideal 347
Appertains, exponent to which an integer 99 393
Associated integers, in k( ) 163 ) 163
Associated integers, in k(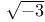 ) 223 ) 223
Associated integers, in k(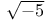 ) 246 ) 246
Associated integers, in R 9;
Basis of conjugate ideals 301
Basis of ideals 293-295
Basis, of ideal 293-295
Basis, of ideal, determination 351-355
Basis, of k( ) 159-161 ) 159-161
Basis, of k(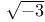 )) 220 )) 220
Basis, of k(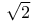 ) 232 ) 232
Basis, of k(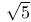 ) 245 ) 245
Basis, of k(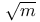 ) 284-287 ) 284-287
Basis, of k(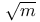 ), determination 289—292 ), determination 289—292
Binomial congruences 110-112
Biquadratic residues and reciprocity law 205-217
Canonical basis of ideals 294
Character of an integer, biquadratic 209 212
Character of an integer, quadratic, in k( ) 212 ) 212
Character of an integer, quadratic, in R 121
Class number of a realm is finite 437
Class number of a realm, definition 434
Class number of a realm, determination 437-448 451
Classes, ideal, definition 432
Classification of the numbers of an ideal with respect to another ideal 326-330
Common divisor of ideals 303
Congruences in k( ) 180 ) 180
Congruences of condition 59-61 190 369-372
Congruences of first degree in one unknown 68-70
Congruences of nth degree in one unknown, preliminary discussion 66-68 374 375
Congruences of second degree with one unknown 119-121
Congruences of two polynomials 57 370
Congruences, 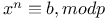 114-116 114-116
Congruences,  -1 -1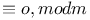 90 387 388 90 387 388
Congruences, common roots 92 93 389
Congruences, composite modulus 95-97 391 392
Congruences, definition 31 297 323
Congruences, determination 93 94 386
Congruences, elementary theorems 32-37 323-326
Congruences, equivalent systems 64;
Congruences, Euler’s criterion 115
Congruences, limit to number of roots 89 386
Congruences, multiple roots, definition 89 386
Congruences, primitive and imprimitive roots 111
Congruences, root 66 374
Congruences, solution of $x^{1}\equiv -1, mod p, by means of Wilson’s theorem 129 130
Congruences, transformations 62-64 372 374
Congruences, with prime modulus 88-90 385-387
Conjugate ideals 301
Conjugate, numbers 4
Conjugate, realm 4
Dirichlet’s theorem regarding infinity of primes in an arithmetical progression 11
Discriminant, of k( ) 161 ) 161
Discriminant, of k(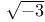 ) 221 ) 221
Discriminant, of k(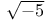 ) 245 ) 245
Discriminant, of k(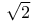 ) 232 ) 232
Discriminant, of k(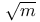 ) 287 288 ) 287 288
Discriminant, of number 284
Divisibility of ideals 263 303
Divisor, greatest common, discussion of definition 252
Divisor, greatest common, in k( ) 173 ) 173
Divisor, greatest common, in R 16 18 25
Divisor, greatest common, of two ideals 310-313 318
Divisors, of integers in R, number of 23
Divisors, of integers in R, sum of 24;
Divisors, of of ideal, number of 318
Equality of ideals 258 259 302
Equivalence of ideals 427-431
Equivalence of ideals in narrower sense 431
Equivalent congruences 62-64 372 373
Eratosthenes, sieve of 10
Euler's criterion for solvability of 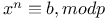 115 122 115 122
Factorization of a rational prime determined by (d/p), in k( ) 179 ) 179
Factorization of a rational prime determined by (d/p), in k(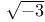 ) 229 ) 229
Factorization of a rational prime determined by (d/p), in k(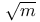 ) 347 348 ) 347 348
Fermat’s theorem 57
Fermat’s theorem as generalized by Euler 57
Fermat’s theorem, analogue for ideals 368 369
Fermat’s theorem, analogue for k( ) 189 ) 189
Frequency of the rational primes 11
Galois realm 281
Gauss’ Lemma 130
General algebraic integers 1 275-279
Generation of realm 3
Ideal numbers, nature explained 254-257
Ideal numbers, necessity for 253
Ideals, definition 257 293
Ideals, determination of basis 298—301
Ideals, introduction of numbers into and omission from symbol 258 295 296
Ideals, numbers defining 295
Ideals, principal and non-principal 260 261 297
Imprimitive numbers see primitive numbers
Incongruent numbers, complete system of, in k( ) 182-185 ) 182-185
Incongruent numbers, complete system of, in k(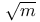 ) 326 ) 326
Incongruent numbers, complete system of, in R 34
Index, of a power 106 399
Index, of a product 106 399
Indices, definition 105 399
Indices, solution of congruences by means of 108—110 400-402
Indices, system of 106 399
Integers, absolute value in R 7 33
Integers, of k( ) 157 ) 157
Integers, of k(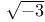 ) 219 ) 219
Integers, of k(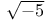 ) 245 ) 245
Integers, of k(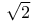 ) 231 ) 231
Integers, of k(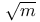 ) 284-287 ) 284-287
Integers, of R 7 23
Legendre’s symbol 127
Multiple, least common, in R 25
Multiple, least common, of two ideals 310-312 318
Multiplication of ideals 261 262 302 303
Non-equivalent ideals, complete system of 434
Norm of ideals 326-338 351
Norm, of a number, determination 351
Norm, of a number, in k( ) 156 ) 156
Norm, of a number, in k(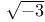 ) 218 221 ) 218 221
| Norm, of a number, in k(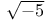 ) 245 ) 245
Norm, of a number, in k(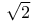 ) 231 ) 231
Norm, of a number, in k(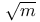 ) 283 ) 283
Norm, of a number, of an ideal, definition 326 337
Norm, of a number, value 330
Norm, of a prime ideal 338
Norm, of a principal ideal 337
Norm, of a product of ideals 334
Number class, ideal modulus 324
Number class, rational modulus 32 33
Numbers of ideals 293
Numbers, algebraic, conjugate 4
Numbers, algebraic, definition 1
Numbers, algebraic, degree of 1
Numbers, algebraic, of k( ) 155 ) 155
Numbers, algebraic, of k(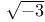 ) 1 218 ) 1 218
Numbers, algebraic, of k(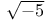 ) 245 ) 245
Numbers, algebraic, of k(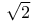 ) 231 ) 231
Numbers, algebraic, of k(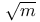 ) 281 ) 281
Numbers, algebraic, of R 7
Numbers, algebraic, of the general realm 271-279
Numbers, algebraic, rational equation of lowest degree satisfied by 2 273
Pell’s equation 423-426
Polynomials in a single variable 268-271
Polynomials with respect to a prime modulus, reduced 62
Polynomials, associated 77 381
Polynomials, common divisor of 76 380
Polynomials, common multiple of 76 380
Polynomials, congruence with respect to a double modulus 81
Polynomials, degree of 76
Polynomials, determination of prime 78 381 382
Polynomials, divisibility of 76 380
Polynomials, division of one by another 382
Polynomials, primary 78 381
Polynomials, prime 78 381
Polynomials, unique factorization theorem for 82-87 382-385
Polynomials, unit 77 381
Power of a prime by which  is divisible 26 is divisible 26
Primary integers of k( ) 193-196 ) 193-196
Prime factors, resolution of an ideal into 348-350
Prime ideals 263-265 304
Prime ideals, determination and classification 339-348
Prime ideals, of k(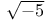 ) 263-265 ) 263-265
Prime ideals, of k(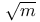 ), definition 304 ), definition 304
Prime numbers, infinite in number 10
Prime numbers, of k( ), classification 177 ), classification 177
Prime numbers, of k( ), definition 165 ), definition 165
Prime numbers, of k(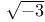 ), classification 227-230 ), classification 227-230
Prime numbers, of k(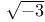 ), definition 223 ), definition 223
Prime numbers, of k(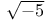 ) 246 247 ) 246 247
Prime numbers, of k(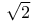 ), classification 238-240 ), classification 238-240
Prime numbers, of k(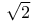 ), definition 235 ), definition 235
Prime numbers, of R, definition 9
Primitive numbers, of k( ) 157 ) 157
Primitive numbers, of k(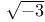 ) 218 ) 218
Primitive numbers, of k(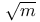 ) 282 283 ) 282 283
Primitive numbers, of the general realm 274 275;
Primitive numbers, with respect to a prime ideal modulus 398
Primitive root, definition 100
Primitive root, determination 112
Primitive root, of prime of form 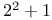 151 151
Primitive root, of prime of form 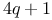 is 2 152 is 2 152
Principal class 432
Product of classes 432
Realm, conjugate 4
Realm, definition 3
Realm, degree 4
Realm, generation 3
Realm, number defining 4 280
Realm, number generating 4
Reciprocal classes 434
Reciprocity law, determination of value of (a/p) by means of 144
Reciprocity law, for biquadratic residues 210 215-217
Reciprocity law, for quadratic residues, in k( ) 201-205 ) 201-205
Reciprocity law, for quadratic residues, in R 135
Reciprocity law, other applications of 149
Residue system, complete, in k( ) 182-185 ) 182-185
Residue system, complete, in R 33 34
Residue system, complete,in k(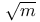 ) 326 ) 326
Residue system, reduced, in k( ) 185 ) 185
Residue system, reduced, in k(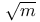 ) 358 ) 358
Residue system, reduced, in R 37
Residue, odd prime moduli of which an integer is a quadratic 128 145 147
Residue, prime moduli of which 2 is a quadratic 133
Residue, prime moduli of which — 1, is a quadratic 128
Residues of powers, complete system of 98 393
Residues of powers, definition 98 392
Residues of powers, law of periodicity 100
Residues, biquadratic 205-217
Residues, cubic 250
Residues, determination of quadratic 124
Residues, n-ic 116
Residues, quadratic non- 121
Residues, quadratic, in k( ) 196-201 ) 196-201
Residues, quadratic, in R 121
Residues, with respect to a series of moduli, integer having certain 70
Rummer’s ideal numbers 267
Sub-realm 157
Symbol of ideals 257 295
Symbol, Legendre’s 127
Symbol, Legendre’s for ideal 257 295
Unique factorization theorem, for ideals in k(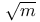 ) 305-317 ) 305-317
Unique factorization theorem, graphical discussion of 169
Unique factorization theorem, in k( ) 167 174 ) 167 174
Unique factorization theorem, in k(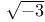 ) 226 ) 226
Unique factorization theorem, in k(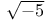 ), failure of 247-253 ), failure of 247-253
Unique factorization theorem, in k(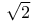 ) 236 237; ) 236 237;
Unique factorization theorem, in R 12
Unique factorization theorem, necessity for 253
Unique factorization theorem, realms in which original method of proof holds 248-250
Unique factorization theorem, restoration in terms of ideal factors 265 266
Unit ideal, of k(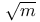 ) 304 ) 304
Unit ideal, of k(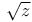 ) 263 ) 263
Unit, fundamental, determination 420-426
Unit, fundamental, of k(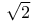 ) 233 ) 233
Unit, fundamental, of k(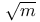 ), definition 420 ), definition 420
Units, of k( ) 163 ) 163
Units, of k(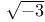 ) 222 ) 222
Units, of k(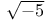 ) 246 ) 246
Units, of k(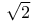 ) 232-235 ) 232-235
Units, of k(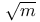 ), definition 403 ), definition 403
Units, of R 8
Units, realm imaginary 404
Units, realm real 405-426
Wilson’s Theorem 91
Wilson’s theorem analogue for ideals 388 389
Wilson’s theorem as generalized by Gauss 91
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
) 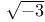 )
) 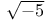 )
) 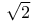 )
) 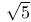 )
) 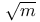 )
) 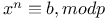
 -1
-1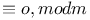
 is divisible
is divisible 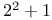
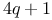 is 2
is 2 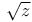 )
)