|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Laurens Jansen — Theory of Finite Groups. Applications in Physics |
|
|
 |
| Предметный указатель |
Isomorphism theorem 37—38
Isomorphism theorem for operator groups 64
k-space 249
k-vector 248—249
k-vector, general 252
k-vector, group of 252
k-vector, special 252
k-vector, star of 255
Kernel of homomorphism 21
Kramers' degeneracy theorem 287
Kramers' degeneracy theorem, generalised 290
Kronecker product of matrices 154n
Kronecker product of representations 154—155 158—159
Lagrange's theorem 15—17
Lattice 238
Lattice, Bravais 353
Lattice, reciprocal 247
Lebesgue square-integrable function space 192
Length of a vector see "Norm"
Linear manifold(s) 193
Linear manifold(s), direct sum of 196
Linear manifold(s), disjoint 196
Linear map 64
Linear operator 86 170 193
Linear subspace see "Subspace"
Linear transformation 64
Little group 143 144
Lorentz group 306—307
Lorentz group, orthochronous 306—307
Lorentz group, proper 307n
Lorentz group, proper orthochronous (or restricted) 307
Lorentz transformation 306
Lorentz transformation, inhomogeneous (or Poincare transformation) 303ff.
Magnetic double point-groups 323
Magnetic point-groups 354 356
Manifold, linear 193
Map, linear 64
Mapping(s) (of groups or sets) of groups 17ff.
Mapping(s) (of groups or sets) of sets 17—18
Mapping(s) (of groups or sets), automorphic 20
Mapping(s) (of groups or sets), endomorphic 20n 59
Mapping(s) (of groups or sets), epimorphic 20n
Mapping(s) (of groups or sets), homomorphic 19ff.
Mapping(s) (of groups or sets), into 18
Mapping(s) (of groups or sets), isomorphic 19ff.
Mapping(s) (of groups or sets), monomorphic 20n
Mapping(s) (of groups or sets), natural 35
Mapping(s) (of groups or sets), one-to-one 18
Mapping(s) (of groups or sets), onto 18
Mapping(s) (of groups or sets), state 193 202
Mapping(s) (of groups or sets), symmetric 163
Maschke's Theorem 95
Matrices, Dirac 292 301
Matrices, kronecker product of 154n
Matrices, Pauli spin 125 263 301
Matrices, unitary unimodular 221
Matrix group(s) 83
Matrix group(s), Dirac 299
Matrix group(s), unitary 83
Metric 86
Metric, Euclidean 86
Module 5 69—70
Module, left and right 69
Module, R- 69
Module, two-sided 69
Module, Z- 62
Monoid 5
Monomorphism (or Monomorphic mapping) 20n
Multiplication law 2
Multiplication table 7
Multiplication, natural 36
Multiplicity of homomorphic mapping 22
Natural homomorphism 37
Natural mapping 35
Natural multiplication 36
Natural projection see "Natural homomorphism"
Natural representation (of 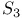 ) 118 ) 118
Norm of a vector 86 190
Normal divisor see "Normal subgroup"
Normal subgroup 22 33—35
normalizer 15
Octahedral group see "Cubic group"
Operator domain of a group 58—59
Operator group (or  -group) 58ff. -group) 58ff.
Operator homomorphism see "Admissible homomorphism"
Operator on a group 59
Operator or Operation 193
Operator or Operation, adjoint see "Operator or Operation hermitian
Operator or Operation, antilincar 170 193
Operator or Operation, antisymmetrization 234
Operator or Operation, antiunitary 195
Operator or Operation, charge conjugation 294 310 314
Operator or Operation, complex conjugation 170 216 281
Operator or Operation, Dirac 292 294
Operator or Operation, domain of 193
Operator or Operation, group projection 225ff.
Operator or Operation, hermitian 194—195
Operator or Operation, hermitian conjugate 86—87 194
Operator or Operation, idempotent 197
Operator or Operation, identity 193
Operator or Operation, inverse 194
Operator or Operation, linear 86 170 193
Operator or Operation, permutation 6 9—10 18 27—29 234—236
Operator or Operation, point- 238 304 306 307 334 335
Operator or Operation, projection 197
Operator or Operation, range of 193
Operator or Operation, reflection (in 3-dimensional Euclidean space) 9 349
Operator or Operation, rotation (in 3-dimensional Euclidean space) 9 27 238 335ff.
Operator or Operation, self-adjoint see "Operator or Operation hermitian"
Operator or Operation, space-group 238ff.
Operator or Operation, space-inversion (in 3-dimensional Euclidean space) 238 334
Operator or Operation, space-inversion (in space-time) 306
Operator or Operation, space-time-inversion 306
Operator or Operation, substitution 213ff.
Operator or Operation, symmetrization 234
Operator or Operation, symmetry 9 189 203ff.
Operator or Operation, time-inversion 305
Operator or Operation, time-reversal 211 281ff. 289 316 356
Operator or Operation, translation 238—239 240
Operator or Operation, unit see "Operator or Operation identity"
Operator or Operation, unitary 193
Operator set see "Operator domain of a group"
Orbit 142—143
Order of conjugation class 30
Order of group 5
Order of group element 14
Orthochronous Lorentz group 306—307
Orthochronous Poincare group 306
Orthochronous point-operation (in space-time) 306
Orthogonal complement of subspace 196
Orthogonal decomposition of vector space or linear manifold 196
Orthogonality relations for characters 103 111
Orthogonality relations for matrix elements 100ff.
Pauli exclusion principle 234—236
Pauli spin matrices 125 263 301
Pauli — Schroedinger Hamiltonian 328
Pauli — Schroedinger Hamiltonian with spin-orbit coupling 262 329
Permutation (operator) 6 9—10 18 27—29
Permutation (operator) for many-particle systems 234—236
Permutation (operator), even and odd 236
Permutation group 6 9—10 115ff. 236
Permutation group in many-particle systems 234—236
Phase-multiplication property 208
Physical representation 208
Poincare group 304ff.
Poincare group, orthochronous 306
Poincare group, proper 307n
Poincare group, proper orthochronous 306
Poincare transformation 303ff.
Point-group(s) 9 334ff.
| Point-group(s), abstract 352
Point-group(s), abstract crystallographic 354
Point-group(s), black-white see "Point-group(s) Shubnikov"
Point-group(s), crystallographic 161 188 217 238 241 334 352ff.
Point-group(s), cubic 347
Point-group(s), cyclic 345 346
Point-group(s), dihedral 346
Point-group(s), double 269
Point-group(s), grey 355
Point-group(s), icosahedral 348
Point-group(s), magnetic 354 356
Point-group(s), magnetic double 323
Point-group(s), octahedral see "Point-group(s) cubic"
Point-group(s), of the k-vector 252
Point-group(s), proper 341 348—349
Point-group(s), Shubnikov 354—355
Point-group(s), substitutional 217
Point-group(s), tetrahedral 347
Point-operation (in 3-dimensional Euclidean space) 238 307 334
Point-operation (in 3-dimensional Euclidean space), improper 238 335
Point-operation (in 3-dimensional Euclidean space), proper (or Rotation) 238 335
Point-operation (in space-time) 304
Point-operation (in space-time), orthochronous 306
Potential, four- 293
Potential, scalar (electric) 293
Potential, vector (magnetic) 293
primary group 55—56
Product of group elements 2
Product of groups or subgroups 39 51 57
Product of groups or subgroups, abstract (or external) direct 43 52 57
Product of groups or subgroups, direct 41 51 57 153ff.
Product of groups or subgroups, infinite 57
Product of groups or subgroups, multiple finite 51
Product of groups or subgroups, semidirect 41 46ff. 60 157ff.
Product of groups or subgroups, weak direct 49
Product, Kronecker, of matrices 154n
Product, Kronecker, of representations 154—155 158—159
Product, scalar 83 86
Projection operator 197
Projection operator, complementary 197
Projection operator, group 225ff.
Projection operator, perpendicular 197
Projection, natural see "Natural homomorphism"
Proper Brillouin zone 258
Proper Lorentz group 307n
Proper orthochronous Lorentz group 307
Proper orthochronous Poincare group 306
Proper Poincare group 307n
Proper point-group 341 348—349
Proper point-operation (or Rotation) in 3-dimensional Euclidean space 238 335
Proper subgroup 13
Quaternions 70—71
Quotient group see "Factor group"
Quotient set 35
Ray of symmetry operators 204ff.
Ray representative 204
Real affine group in 3 dimensions 241
Real orthogonal group in 3 dimensions see "Rotation-inversion group"
Real orthogonal representation 85
Real representation 85
Reciprocal lattice 247
Reciprocal space 247
Reduced wave vector see "k-vector"
Reduced zone see "First Brillouin zone"
Reducible co-representation 173
Reducible representation 79 80 92ff.
Reduction of operator 199
Reflection (in 3-dimensional Euclidean space) 9 349
Reflexive property of equivalence relation 24
Regular representation 80 135
Representation space see "Carrier space"
Representation(s) 76ff.
Representation(s), allowable 149
Representation(s), alternating 236
Representation(s), associate 149
Representation(s), carrier space for 79
Representation(s), character (vector) of 97
Representation(s), commuting ring of 100
Representation(s), completely decomposed 95
Representation(s), completely reduced 94
Representation(s), complex conjugate of 125ff.
Representation(s), conjugate 142
Representation(s), decomposable 94
Representation(s), double-valued see "Representation(s) spin"
Representation(s), engendered 152
Representation(s), equivalent 83
Representation(s), extra 273—274
Representation(s), faithful 76
Representation(s), identity 77 112
Representation(s), indecomposable 94
Representation(s), induced 133—135 138ff.
Representation(s), irreducibility 79 80 92ff.
Representation(s), irreducible criterion for 107
Representation(s), Kronecker product of 154—155 158—159
Representation(s), natural (of 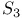 ) 118 ) 118
Representation(s), physical 208
Representation(s), real 85
Representation(s), real orthogonal 85
Representation(s), reducible 79 80 92ff.
Representation(s), regular 80 135
Representation(s), spin 268
Representation(s), subduced 133 135ff.
Representation(s), trivial see "Representation(s) identity"
Representation(s), unitary 83
Resolution of the identity 198
Resolution of the identity, associated with group of operators 199 226 227
Resolution of the identity, associated with hermitian operator 200—201
Restricted Lorentz group see "Proper orthochronous Lorentz group"
Restriction of operator 200
Ring 5 67
Ring homomorphism 67
Ring of matrices 68 100
Ring of quaternions 70—71
Ring with unit element 67
Ring, center of 68
Ring, commuting (of representation) 100
Ring, division see "Field"
Rotation (in 3-dimensional Euclidean space) 9 27 238 335ff.
Rotation group in 3 dimensions 27 335
Rotation-inversion group in 3 dimensions 307 334
Scalar product (hermitian) 83 86
Schur — Auerbach theorem 83
Schur's Lemmas 98—99
Self-adjoint operator see "Hermitian operator"
Self-conjugate subgroup see "Normal subgroup"
Semidirect product of groups 41 46ff. 60
Semidirect product of groups, irreducible representations of 157ff.
Semigroup 65
Separable Hilbert space 191
Set(s) 1
Set(s) with structure 1
Set(s), disjoint 13
Set(s), intersection of 12
Set(s), quotient 35
Set(s), union of 12
Shubnikov point-groups 354—355
Similarity transformation of group see "Conjugation"
Similarity transformation of representation 83
Simple group 34
Single group 205
Skew field 70
Space see "Vector space"
Space-group (crystallographic) 118 217 233 236ff.
Space-group (crystallographic), double 243 261ff.
Space-group (crystallographic), substitutional 217 242—243
Space-group (crystallographic), symmorphic 161 241 242
Space-group operator 238ff.
Space-group operator, substitution 242
Space-inversion operator (in 3-dimensional Euclidean space) 238 334
Space-inversion operator (in space-time) 306
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



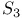 )
)  -group)
-group)