|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Alon N., Spenser J. Ч The probabilistic method |
|
|
 |
| ѕредметный указатель |
Margulis 137Ч138 142
Marica 84
Markov 57 101 162 264 266
Markov chain 162
Martingale 2 vii 93Ч100 102Ч104 108Ч109
Martingale, Doob process 95
Martingale, edge exposure 94Ч97
Martingale, flip a coin 95
Martingale, inequality vii 95 101 111
Martingale, vertex exposure 95Ч96 99
Matousek 226
Matrix, adjacency of a graph 137 139Ч140 143Ч144
Matrix, adjacency of a tournament 61
Matrix, Hadamard 207Ч208
Matula 5Ч6 52
Maurey 95 99
Mean 35Ч36 42 44 96 102 105 109Ч110 115 124 126Ч127 129 162 164Ч166 168 201 264 268Ч270
Mean, geometric 22Ч24
Meet 83 89
Meir 217Ч218
Miklos 278
Milman 95 99 137Ч138
Minc 22 60
Monochromatic 1Ч3 6Ч7 16Ч17 20Ч21 26 30Ч33 65 67 69 75Ч76 199 249Ч250 254Ч255 257 276Ч277
Moon 4 134
Nakayama 70
Naor 257
NC 253Ч254 256
Nesetfil 278
Newborn 259
Nilli 138
Normal, distribution 19 42 44Ч45 102 209 267Ч269 271 276
NP(non-deterministic polynomial time) 184 191 194Ч195
P(polynomial time) 2
Pach 68 223 226
Packing 29Ч30 34 36Ч37 54 229
Packing of 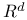 230 230
Packing, constant 29 229
Packing, greedy 34
Packing, number 37 54
Packing, random 34
Paley 148
Parity function 183 188Ч190 194 196
Partially ordered set 83 88Ч90
Paturi 219
Paul 185
Peralta 257
Perles 221
Permanent 22Ч23 60Ч61
Peroche 70
Pessimistic estimators 251
Phase transition 161 168
Phillips 138 142
Pinsker 137
Pintz 28Ч29
Pippenger 54
Pittel 168
Podderyugin 5Ч6
poisson 35Ч36 115 119 121 123Ч124 127Ч128 156 162 164Ч166 168 269Ч270
Primality testing algorithm 141
Prime 9 21 28 42Ч45 59 72 134 138 141Ч142 148 189 276
Projective plane 246
Property of graphs 88
Pythagoras 20 216
Quadratic residue character 135
Quasi-random 134
Rabin 141
Radhakrishnan 7 30
Rado 12 277
Radon 222
Raghavan 250Ч251
Ramachandran 253
Ramanujan 42 139
Ramsey 1 10 16 25Ч26 37 67 133Ч134 273 275Ч277 280
Ramsey theorem 275 277
Ramsey, function 277
Ramsey, graph 133Ч134
Ramsey, graph, explicit construction 133
Ramsey, number 1 10 25Ч26 37 67 273 276
Ramsey, theory 16 280
Random process, walk 93 142 150Ч151
Random variables 4 10Ч11 13 18Ч19 21 41Ч42 44 58Ч59 93 101 103 106 108 115 117 126Ч127 146 162 197 237 240 242Ч243 245 254Ч257 263Ч264 270 272
Random variables, almost d-wise independence 257
Random variables, binomial 72 113 124 188 220 224
Random variables, d-wise independence 253Ч257
Random variables, decomposition 13 42 75
Random variables, entropy 240
Random variables, indicator 4 13Ч14 26Ч27 42 48 51 56Ч57 91 116 119 121 181 197 200 202 220 235Ч236 246 268Ч269
Random variables, standard normal 271
Range space 220Ч223 225Ч226 228
Razborov 189 191Ч192
| Recoloring 30
Renyi 49 155Ч156 161 276
Riemann 136 229
Rival 88
Rodl 37 53Ч54 136 142 219 278
Rodl nibble 53 105
Ronyai 226
Rooted graph 111 174
Roth 126
Rothschild 26
Sands 88
Sarnak 138 142
Sauer 221
Saxe 185
Schechtman 95 99
Schiitte 3 136
Schonheim 84
Schrijver 22
Schwarz 135 139Ч140 148
Second moment method 41Ч42 47 53Ч54 168
Selfridge 250 277
Shamir 96
Shannon 231Ч233
Shearer 65 242 244 272
Shelah 171 221
Shepp 88
Simon 219
Simonovits 244
Simons 93
Sipser 185
Sloane 255
Smolensky 189
Sorting network 137
Sos 244 278
Spencer 26Ч27 34 36 54 67 73 96 101 104 117 121 125 134 136 171 201 204 250 260 279
SpencerТs theoren 171
Srinivasan 7 30
Steiner 54
Stirling 19 43 61
Sturtevant 242
Subbotovskaya 194Ч195
Suen 128Ч129
Sum-free 8Ч9
Szabo 226
Szekely 260
Szekeres 4 275 278Ч279
Szele 2 14 60
Szemeredi 28Ч29 137 140 259Ч261 272Ч273 277
Szonyi 278
Tactical configuration 54
Talagrand 105
Talanov 171
Tanner 137
Tarjan 6
Tetali 127 276
Thomason 142
Threshold function 47Ч49 120Ч121 124 129 156Ч157 171Ч172 178
TikhonovТs Theorem 66
Tournament 3Ч4 11 14 60Ч63 134Ч136
Tournament, explicit construction 4 136
Tournament, quadratic residue tournament 134Ч135 148
Trotter 260
Turan 27Ч28 42 44 91Ч92 277
TuranТs Theorem 27Ч28 91Ч92
Ullman 2
Valtr 217
Vapnik 221Ч222
Variance vii 18 41Ч42 44 55Ч56 58Ч59 101Ч102 146 188 201 224 267Ч268 270
VC-dimension viii 220Ч225 227
Vector, imbalanced 209
Vertex transitive graph 150Ч151
Vesztergombi 204
Vizing 194
Vu 110Ч111
Walk 140Ч142 144 151
Walk, random 93 142 150Ч151
Wegener 185
Weierstrass 113
Weil 136 139 148
Welzl 221 223 225Ч226
Wendel 215
Wernisch 226
Whitney 243
Wigderson 140 185
Wilson 134 136 142
Witness 141Ч142
Woeginger 223
Wright 170
XYZ-theorem 89
Yao 185
Zero-one laws 171Ч174 178
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте