|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Carmichael R.D. — Diophantine Analysis |
|
|
 |
| Предметный указатель |
Abel 90
Abelian Formulas 87—90
Aubry 83 84 113 116
Avillez 52
Bachmann 116
Barbette 85
Barisien 115
Bernstein 102
Binet 65
Biquadratic Equations 44—48 74—84
Carlini 102
Carmichael 30 39 42 83 88 91 114
Catalan 52
Cauchy 5 100 115
Cubic equations 55—73
Cunningham 114
Davis 52 115
Dcsboves 112 114
Delannoy 72
Descent, infinite see “Infinite Descent”
Development of Method 6—8
Dickson 99
Diophantine Equation, Definition of 1
Diophantine System, Definition of 1
Diophantus 4 5 9 104 106 107 108 111 112 113
Dirichlet 5
Domain, Multiplicative 24—54
Double Equations 78 107
Eisenstein 5
Equation of Pell 26—34
Equations of Fourth Degree 44—48 74—84
Equations of Higher Degree 85—103
Equations of Second Degree 1—44
Equations of third degree 55—73
Equations, Double 78 107
Equations, functional 104—111
Equations, Triple 107
Euclid 9
Euler 5 22 65 68 80 82 112
Evans 113
Fauquembergue 83
Fermat 5 6 7 9 14 39 60 74 77 78 86 88 104 106 107 108 114 115
Fermat problem 86—103
Fermat’s Last Theorem 86
Fleck 103
Frolov 116
Fujiwara 65
Functional Equations, Method of 104—111
Furtwangler 101 102
Gauss 5
Genocchi 115
Gerono 72 112
Gfirardin 116
Haentzschel 62
Hart 112
Hayashi 103
Hecke 102
Hillyer 23
Historical remarks 4—8 9
Holm 114
Holmboe 90
Hurwitz 102 115
Infinite descent, method of 14 18—22
| Integral solution 2
jacobi 5
Jonqui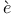 res 112 res 112
Kapferer 103
Kellogg 115 116
Kummer 100 101
Lagrange 50
Lebesgue 52
legendre 50 73 90 99 112 115
Lehmer 13
Lind 102
Liouville 102
Longchamps 116
Lucas 6 52 53 112
Maillet 99 103 114
Martin 52 81 85 113 114 115
Mathews 5
Method of Functional Equations 104—111
Method of infinite descent 14 18—22
Method of Multiplicative Domain 24—54
Method, Development of 6—8
Meyer 115
Meyl 112
Miot 113
Mirimanoff 99 101 102
Moret — Blanc 83
Moureaux 52
Multiplicative Domain 24—54
Paraira 84
Pell equation 26—34
Pepin, S 3 80 83 112 114
Pietrocola 83
Plato 9
Primitive solution 2
Pythagoras 8 9
Pythagorean triangles see “Triangles”
Quadratic equations 1—44
Rational solution 2
Rational Triangles see “Triangles”
Realis 44 73 115
Schaewen 59
Schwering 65
smith 100
Solution of Diophantine Equation 2
Solution, integral 2
Solution, Primitive 2
Solution, Rational 2
Stormer 114
Swinden 113
Thomson 115
thue 53 116
Triangles, Numerical 8
Triangles, Primitive 8
Triangles, Pythagorean 8 9—11 17 21 22 33 77 80 103 112 113
Triangles, Rational 8—13
Triple equation 107
Valroff 112
Vandiver 101 102
Visschers 115
Wallis 114
Welmin 113 114
Werebr ssov 53 72 ssov 53 72
Whitford 33
Wieferich 101
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



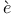 res
res  ssov
ssov