|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| W. Burnside — Theory of Groups of Finite Order |
|
|
 |
| Предметный указатель |
Abel 99
Abelian group 24
Abelian group of order 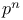 and type (1, 1,..., 1), group of isomorphisms of 89 and type (1, 1,..., 1), group of isomorphisms of 89
Abelian group of order 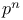 and type (1, 1,..., 1), holomorph of 90 and type (1, 1,..., 1), holomorph of 90
Abelian group of order 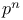 and type (1, 1,..., 1), number of sub-group of given order of 84 and type (1, 1,..., 1), number of sub-group of given order of 84
Abelian group of order 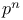 and type (1, 1,..., 1), number of ways of choosing a set of independent generating operations of 85 and type (1, 1,..., 1), number of ways of choosing a set of independent generating operations of 85
Abelian group, characteristic series of 82
Abelian group, existence of independent generating operations of 77
Abelian group, is direct product of groups whose orders are powers of primes 75
Abelian group, orders of the isomorphisms of 86
Abelian group, sub-groups of 78—81 84
Abelian group, symbol for, of given type 80
Alternating group 132
Alternating group of degree 5, represented as an irreducible group in 3 symbols 232
Alternating group, group of isomorphisms of 162
Alternating group, is simple except for degree 4 139
Baker 358
Blickfeldt 348 352
Bochert 180
Bolza 188
Burkhardt 485
Burnside 91 122 163 166 184 243 269 306 311 323 328 353 452 464 468 485
Castelnuovo 360
Cauchy 47
Cayley 423
Central of a group 27
Characteristic equation of a linear substitution 192
Characteristic of a linear substitution 192
Characteristic series 69
Characteristic series of an Abelian group 82
Characteristic series, invariance of factor-groups of 69
Characteristic sub-group 68
Characteristic sub-group, groups with no, are either simple or the direct product of simply isomorphic simple groups 68
Chief composition-series 51
Chief composition-series or chief-series, examples of 55 56
Chief composition-series or chief-series, invariance of factor-groups of 51
Circular permutation 9
Cole 504
Cole and Glover 80
Colour group 305
Commutator 38
Commutator sub-group 39
Complete group 70
Complete group, group of isomorphisms of a simple group of composite order is a 71
Complete group, groups which contain a, self-conjugately are direct products 70
Complete group, if an Abelian group of odd order is a characteristic sub-group of its holomorph, the latter is a 72
Complete group, symmetric group is a, except for degree 6 162
Completely reduced form of a transitive group 207
Completely reducible group 197
Composite group 24
Composition of two groups of linear substitutions 191
Composition-factors 48
Composition-series 48
Composition-series, examples of 55 56
Composition-series, invariance of factor-groups of 50
Conjugate groups of linear substitutions 190
Conjugate groups of linear substitutions, are simply isomorphic 190
Conjugate groups of linear substitutions, possess an invariant Hermitian form 195
Conjugate operations 24
Conjugate set of operations 26
Conjugate sets, invariant property of multiplication table of 236
Conjugate sets, multiplication of 41—46
Conjugate sub-groups 24
Cycle of a permutation 4
Cyclical group 22
Cyclical group, group of isomorphisms of 88
Cyclical group, holomorph of 88
Dedekind 146
Defining relations of a group for groups of genus one 302
Defining relations of a group for groups of genus two 302
Defining relations of a group for groups of genus zero 296
Defining relations of a group for groups of order 24 126
Defining relations of a group for groups of order 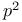 , , 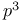 , , 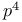 117 117
Defining relations of a group for groups of order  59 59
Defining relations of a group for groups of order pq 36
Defining relations of a group for groups whose Sylow sub-groups are cyclical 129
Defining relations of a group for the holomorph of a cyclical group 88
Defining relations of a group for the simple group of order 168 303
Defining relations of a group, limitations on the number of, when the genus is given 291
Degree of a permutation-group 131
Derived group 39
Derived groups, properties of 39
Derived groups, series of 40
Determinant of a linear substitution 188
Dickson 428 485 504
Dihedral group 295
Direct product of two groups 31
Direct product, of two groups represented as a transitive group 152
Direct product, of two simply isomorphic groups of order n without self-conjugate operations represented as a transitive group of degree n 64 136
Distinct representations 174 204
Doubly transitive group has two irreducible components 250
Doubly transitive group of degree 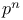 and order and order  140 140
Doubly transitive group with a complete set of triplets 169
Doubly transitive group, is in general simple or contains a simple self-conjugate sub-group 154
Doubly transitive group, the sub-groups of, which keep two symbols fixed 167
Dyck 44 231 372 383 401 409 418 422
Elliott 289
Equivalent representations 174 204
Even permutation 11
Factor-group 29
Family of irreducible representations 234
Forsyth 397 400
Fractional linear group 314
Fractional linear group, analysis of 315—327
Fractional linear group, generalization of 328
Frobenius 39 45 49 53 92 93 108 122 129 149 153 173 269 328 331 334 502
Galois 202 451
Generalized linear homogeneous group 882
Genus of a group 289
Gierster 428
Graphical representation, of a cyclical group 276
Graphical representation, of a general group 277—280
Graphical representation, of a group of finite order 287 288 291
Graphical representation, of a special group 281—286
Graphical representation, of groups of genus one 298—301
Graphical representation, of groups of genus zero 295
Graphical representation, of the simple group of order 168 303
Group 12
Group of isomorphisms 62
Group of isomorphisms of a cyclical group 88
Group of isomorphisms of au Abelian group of order 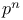 and type (1, 1, ..., 1) 89 and type (1, 1, ..., 1) 89
Group of isomorphisms of the alternating group 162
Group of isomorphisms, general properties of 62—67
Group of monomial substitutions 242
Group-characteristics, calculation of 222 223
Group-characteristics, congruences between 256 257
Group-characteristics, relations between 211—216 218 219
Groups of linear substitutions of finite order are irreducible or completely reducible 200
Groups of linear substitutions, composition of 191
Groups of linear substitutions, general properties of 188
Groups of linear substitutions, self-conjugate operations of 202 203
Groups of linear substitutions, standard form of 196
Groups of order 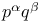 , characteristic sub-groups of 241 , characteristic sub-groups of 241
Groups of order 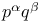 , where p and q are primes, are simple 240 , where p and q are primes, are simple 240
Groups whose order is 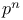 are distinct from their derived groups 94 are distinct from their derived groups 94
Groups whose order is 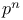 which contain a cyclical sub-group of order which contain a cyclical sub-group of order  self-conjugately 109—111 self-conjugately 109—111
Groups whose order is 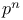 with only one sub-group of given order 104 105 with only one sub-group of given order 104 105
Groups whose order is 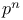 , always have self-conjugate operations 92 , always have self-conjugate operations 92
Groups whose order is 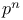 , every sub-group of, is contained self-conjugately in a sub-group of greater order 96 , every sub-group of, is contained self-conjugately in a sub-group of greater order 96
Groups whose order is 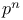 , irreducible representations of, can be expressed as monomial groups 258 , irreducible representations of, can be expressed as monomial groups 258
Groups whose order is 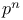 , number of sub-groups of given order is congruent to 1 (mod. p) 103 , number of sub-groups of given order is congruent to 1 (mod. p) 103
Groups whose order is 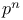 , types of, when n = 2, 3, 4 112—117 , types of, when n = 2, 3, 4 112—117
Groups whose order is 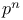 , where p is prime, general properties of 92 , where p is prime, general properties of 92
Groups whose Sylow sub-groups are cyclical 128 129
Heffter 224
Hermitian form 194
Hermitian forms, invariant for group and its conjugate 195
Hermitian forms, number of, for given group of linear substitutions 206
hilbert 606
Hilton 101 427
| Hoelder 39 65 80 84 94 95 146 166 209 210 604
Holomorph of a cyclical group 88
Holomorph of a group 64
Holomorph of an Abelian group of order 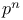 and type (1, 1, ..., 1) 90 and type (1, 1, ..., 1) 90
Holomorph of any Abelian group 87
Holomorph, general properties of 64
Homogeneous linear group, composition-series of 811—813
Homogeneous linear group, general properties of 308—310
Homogeneous linear group, generalization of 332 333
Homogeneous linear group, represented as a doubly transitive group 329
Hurwitz 397 399
Icosahedral group 295
Identical isomorphism 61
Identical operation 13
Identical representation 205
Imprimitive group 146
Imprimitive self-conjugate sub-group of a doubly transitive group 151
Imprimitive systems of a regular permutation-group 176
Imprimitive systems of any transitive group 177
Imprimitive systems, properties of 147 148
Inner isomorphism 63
Intransitive group 133
Intransitive groups, general properties of 142—144
Intransitive groups, test for 145
Intransitive groups, transitive constituents of 142
Invariant of a group of linear substitutions 260
Invariants of a group of linear substitutions of an irreducible group 269
Invariants of a group of linear substitutions, absolute and relative invariants 260
Invariants of a group of linear substitutions, examples of 266—268
Invariants of a group of linear substitutions, quadratic 270
Invariants of a group of linear substitutions, system of, in terms of which all are rationally expressible 263
Inverse conjugate sets 41
Inverse of an operation 12
Irreducible components of a group of linear substitutions 205
Irreducible group of linear substitutions 197
Isomorphism 61
Isomorphisms, limitation on the order of 86
Isomorphisms, of a general and a special group 275
Isomorphisms, of a group with itself, inner and outer 63
Isomorphisms, which change every conjugate set into itself 65 249
Isomorphisms, which leave no operation except E unchanged 66 248
JORDAN 22 65 99 172 176 178 180 198 204 207 428 455 485
Klein 407
Klein and Fricke 188
Linear homogeneous group 90
Linear substitution 188
Loewy 243 256 266
Maclagan-Wedderburn 45
Maillet 163
Marggraff 207
Mark of a sub-group of a permutation-group 180
Maschke 243 427
Mathieu 182
Maximum self-con jugate sub-group 27
Maximum sub-group 27
Metabelian group 40
Miller 98 134 147 161 503
Minimum self-conjugate sub-group 52
Minimum self-conjugate sub-group, is a simple group or the direct product of simply isomorphic simple groups 53
Minkowski 484 506
Molien 300
Moore 224 256 452 464 468
Multiplication table of conjugate sets 44
Multipliers of a linear substitution 193
Multiply isomorphic groups 28
Multiply transitive group 137
Multiply transitive groups, examples of 141
Multiply transitive groups, general properties of 137 138
Multiply transitive groups, self-conjugate sub-groups of 150
Netto 171 207 224
Number of operations whose nth powers are conjugate to a given operation 37
Octohedral group 295
Odd permutation 11
Order of a group 15
Order of a permutation 8
Outer isomorphism 63
Permutable groups 33
Permutable groups, general properties of 34 35
Permutable operations 12
Permutation 2
Permutation-group, doubly transitive, of degree 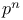 and order and order  140 140
Permutation-group, general properties of 131
Permutation-group, limits to the degree of transitivity 138 160
Permutation-group, order of k-ply transitive, whose degree is n, is a multiple of n(n - 1)...(n - k + 1) 137
Permutation-group, quintuply transitive, of degree 12 173
Permutation-group, representation of a group as 174
Permutation-group, transitive, whose order is the power of a prime 173
Permutation-group, transitive, whose permutations displace all or all but one of the symbols 134 247
Permutation-group, triply transitive, of degree 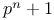 and order and order  141 141
Permutations which are permutable, with a given permutation 170
Permutations which are permutable, with every permutation of a given group 171
Permutations which are permutable, with every permutation of a regular permutation-group 20 136
Primitive group 146
Primitive groups of degrees 3 to 8 166
Primitive groups with transitive sub-group of smaller degree 158 159
Primitive groups, general properties of 147 177
Primitive groups, limit to order of, for given degree 160
Primitive groups, simply transitive, of prime degree, are soluble 251
Primitive groups, test for 147
Primitive groups, when soluble have the power of a prime for degree 154
Quadratic group 321
Quaternion group 106
Reduced variables 205
Reducible group of linear substitutions 197
Regular permutation 9
Relative invariant of a group of linear substitutions 260
Representation of a group as a group of linear substitutions 204
Representation of a group as a group of monomial substitutions 242
Representation of a group as a permutation-group 174
Representation of a group, as a permutation-group 174
Rietz 603
schur 311
Self-conjugate operation 24
Self-conjugate operation, of a transitive permutation-group 135
Self-conjugate operation, of an irreducible group of linear substitutions 202
Self-conjugate sub-group 24
Self-conjugate sub-group, determined by congruences between the group-characteristics 256 257
Self-conjugate sub-group, generated by a complete set of conjugate operations 27
Self-conjugate sub-group, of a primitive group must be transitive 149
Self-conjugate sub-group, of an imprimitive group 146 148
Self-conjugate sub-group, of an intransitive group 142
Series of derived groups 40
Set of generating operations 18
Set of group-characteristics 212
Similar permutations 10
Simple group 24
Simple group of order 168 represented as an irreducible group in 3 variables 232
Simple groups, group of isomorphisms of, is complete 71
Simple groups, order if even is divisible by 12, 16 or 56 245
Simple groups, systems of 139 328 329 332
Simply isomorphic groups 19
Simply isomorphic groups, concrete examples of 17
Soluble group 40 68
Sommer 506
Sub-group 22
Sylow 119 149
Sylow's theorem 120
Sylow's theorem, deductions from 122—125
Sylow's theorem, generalization of 121
Symmetric group 132
Symmetric group, is a complete group, except for degree 6 162
Tetrahedral group 295
Transitive group 133
Transposed groups of linear substitutions 190
Transposition 11
Transpositions, number of, which enter in a permutation is either always even or always odd 11
Transpositions, representation of a permutation by means of 11
Type ( ) of Abelian group 80 ) of Abelian group 80
Weber 99 269 506
Western 80
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



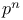 and type (1, 1,..., 1), group of isomorphisms of
and type (1, 1,..., 1), group of isomorphisms of 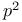 ,
, 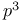 ,
, 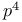


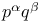 , characteristic sub-groups of
, characteristic sub-groups of  self-conjugately
self-conjugately 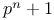 and order
and order 
 ) of Abelian group
) of Abelian group