|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Altman A., Kleiman S. — Introduction to Grothendieck duality theory |
|
|
 |
| Предметный указатель |
 (l an immersion) VI 1.21 (l an immersion) VI 1.21
 (X a flat cover of Y) VI 6.5 (X a flat cover of Y) VI 6.5
 (k an artinian ring, (k an artinian ring, 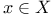 a curve over k) VIII 1.6 a curve over k) VIII 1.6
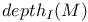 , ,  , depth(M) (M an A-module, I an ideal) IV 3.9 3.11 , depth(M) (M an A-module, I an ideal) IV 3.9 3.11
 (A a k-algebra, M an A-module) VI 1.1 (A a k-algebra, M an A-module) VI 1.1
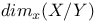 , ,  (f a morphism from X to Y, (f a morphism from X to Y, 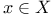 ) VII 1.3 ) VII 1.3
 ( X a flat cover of Y) VI 6.5 ( X a flat cover of Y) VI 6.5
 (E a locally free sheaf) IV 2.6 (E a locally free sheaf) IV 2.6
 II 4.14 II 4.14
 II 4.13 II 4.13
 , , 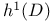 , , , ,  (F a Module, D a divisor) VIII 1.1 (F a Module, D a divisor) VIII 1.1
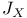 (X an algebraic curve) VIII 1.14 (X an algebraic curve) VIII 1.14
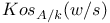 VIII 2.5 VIII 2.5
 , ,  , ,  , , 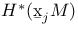 (M an A-module, (M an A-module,  ) I ) I
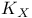 (X a ringed apace) VII 3.2 (X a ringed apace) VII 3.2
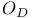 (D a divisor) VII 3.6 (D a divisor) VII 3.6
 (x a ringed space, D a divisor) VII 3.4 (x a ringed space, D a divisor) VII 3.4
 , , 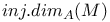 (M an A-module) III 5.1 (M an A-module) III 5.1
 , ,  (M an A-module, p a prime, (M an A-module, p a prime,  ) II 3.9 ) II 3.9
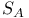 (A a ring) VIII 2.3 (A a ring) VIII 2.3
 (k a field, A a k-algebra) III 2.6 (k a field, A a k-algebra) III 2.6
 ( (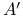 an A-algebra) VIII 3.7 an A-algebra) VIII 3.7
 , ,  , df(x) (f a morphism from X to Y, , df(x) (f a morphism from X to Y, 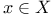 ) VII 5.4 ) VII 5.4
 , , 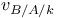 (A a k-algebra, B an A-algebra) VI 1.5 (A a k-algebra, B an A-algebra) VI 1.5
 (F a Module) IV 1.2 (F a Module) IV 1.2
![$[A, Hom_k (M,N)]$](/math_tex/f2991245a7e1f504fefc48bb747324bf82.gif) (A a k-algebra, M, N A-modules) VIII 2.1 (A a k-algebra, M, N A-modules) VIII 2.1
 II 4.10 II 4.10
 , ,  (M an A-module) II 4.1 (M an A-module) II 4.1
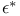 IV 5.2 IV 5.2
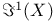 (X a locally noetherian scheme) VII 3.1 (X a locally noetherian scheme) VII 3.1
 (F a locally free sheaf) VI 6.5 (F a locally free sheaf) VI 6.5
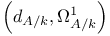 (A a k-algebra) VI 1.3 (A a k-algebra) VI 1.3
 ( ( a polynomial) II 4.11 a polynomial) II 4.11
 ( ( a protective system) II 1.6 a protective system) II 1.6
 (X a Y-scheme) VI 6.4 (X a Y-scheme) VI 6.4
 (N a filtered module) II 1.7 (N a filtered module) II 1.7
 VII 5.14 VII 5.14
Ann(x) II 3.1
Arithmetic genus VIII 1.17
Artinian (ring, module) II 4.4
Ass(m), Ass(F) (M a module, F a module) II 3.1
Associated graded ring , module II 1.4
Associated prime II 3.1
Branch locus VI 6.3
c,  , ,  VIII 1.16 VIII 1.16
Canonical divisor VIII 1.11
Cartan — Eilenberg resolution IV 2.1
codim(Y,X) (Y a closed subscheme of X) V 2.9
Codimension V 2.9
Cohen — Macaulay module III 4.1
Complete intersection III 4.4
Composition series II 4.1
Conormal sheaf VI 1.21
Constructible V 4.1
Cover VI 6.1
cyc,  VII 3.9 VII 3.9
Cycle map VII 3.8
d(M), s(M) III 1.1
deg(D) (D a divisor) VIII 1.4
Degree VIII 1.3
Depth III 3.9 3.12
Differential, 1-differential, differential pair VI 1.3
dim(X) ,  , dim(M) (X a topological space , M an A-module) III 1.1 , dim(M) (X a topological space , M an A-module) III 1.1
DIMENSION III 1.1
Discrete valuation ring VII 2.4
Discriminant VI 6.5
Div(X) (X a ringed space) VII 3.2
Divisor VII 3.2
Divisorial cycle VII 3.1
Effective divisor VII 3.5
Embedded component, prime, prime cycle II 3.1
Equidimensional III 1.1
Essential prime II 3.1
Etale morphism VI 4.1
Euler — Poincare characteristic function VIII 1.1
Factorial domain VII 2.15
Faithful V 1
| Faithfully flat V 1.3 2.1 2.5
Filtration II 1.1
Flat V 2.1 2.5
Generically reduced VII 2.2
Generisation V 2.6
Geometric genus VIII 1.17
gl.hd(A) (A a ring) III 5.3
Global homological dimension III 5.4
gr*(M) ,  (M a filtered A-module , q an ideal) II 1.4 (M a filtered A-module , q an ideal) II 1.4
Graded ring, module II 1.
Height III 3.1
Hilbert characteristic function II 4.10
Hilbert — Samuel polynomial II 4.14
Ideal of definition III 1.2
Infective dimension III 5.1
Irredundant II 3.13
J(F), 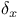 VIII 1.9 VIII 1.9
J(X) (X a locally noetherian scheme) VII 3.1
k-derivation VI 1.1
Kaehler different VI 6.4
Kes VIII 1.14
Koszul complex I 4.1
Length II 4.1
Locally factorial scheme VII 2.15
Locally principal divisorial cycle VII 3.9
M-quasi-regular III 3.3
M-regular III 3.1
Meromorphic functions VII 3.2
Minimal prime II 3.11
Nilradical II 2.8
Noetherian topological space V 4.1
Normal domain VII 2.6
p-primary II 3.12
Pic(X) (X a ringed space) VII 3.7
Picard group VII 3.7
Polynomial morphism VII 1.1
Positive VII 3.1
Primary decomposition II
Prime cycle II 3.11
Prime divisor cycle VII 3.1
Projective limit II 1.6
Protective dimension III 5.1
Pseudo-differential VIII 1.9
Q(M,n) II 4.11
Q(p) (p a prime ld^ai) II 3.14
q-adic filtration II 1.1
q-good filtration II 1.11
Quasi-faithfully flat V 2.5
Quasi-finite VI 2.1
Quasi-flat V 2.5
rad(A) (A a ring) II 1.20
Radical morphism VI 5.1
Reduced VI 3.2
Regular immersion III 4.4
Regular local ring, regular parameters III 4.6
Relative dimension VII 1.3
Residue map VIII 1.14
Saturation II 3.16
Scheme with property  VII 2.1 VII 2.1
Second fundamental form I 3
Separable polynomial VI 6.11
Separated II 1.1
Separated completion II 1.7
Sheaf of 1-differential forms VI 1.21
Sheaf of rational pseudo-differentials VIII 1.12
Smooth morphism VII 1.1
Spectral sequence of a composite functor IV 2.2
Supp(F), Supp(M) (F a sheaf, M a module) II 2.1
Support II 2.1
Tangent space VII 5.4
tr,Tr VI 6.5
Trace VI 6.5
Uniformizing parameter VII 2.4
Unranified morphism VI 3.1
V VII 2.3
V(J) (J a sheaf of ideals) II 2.5
Yoneda pairing IV 1.1
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 (l an immersion)
(l an immersion)  (X a flat cover of Y)
(X a flat cover of Y)  (k an artinian ring,
(k an artinian ring, 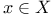 a curve over k)
a curve over k) 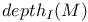 ,
,  , depth(M) (M an A-module, I an ideal)
, depth(M) (M an A-module, I an ideal)  (A a k-algebra, M an A-module)
(A a k-algebra, M an A-module) 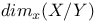 ,
,  (f a morphism from X to Y,
(f a morphism from X to Y,  ( X a flat cover of Y)
( X a flat cover of Y)  (E a locally free sheaf)
(E a locally free sheaf) 

 ,
, 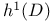 ,
, ,
,  (F a Module, D a divisor)
(F a Module, D a divisor) 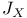 (X an algebraic curve)
(X an algebraic curve) 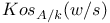
 ,
,  ,
,  ,
, 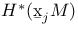 (M an A-module,
(M an A-module,  )
) 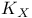 (X a ringed apace)
(X a ringed apace) 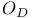 (D a divisor)
(D a divisor)  (x a ringed space, D a divisor)
(x a ringed space, D a divisor)  ,
, 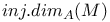 (M an A-module)
(M an A-module)  ,
,  (M an A-module, p a prime,
(M an A-module, p a prime,  )
) 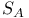 (A a ring)
(A a ring)  (k a field, A a k-algebra)
(k a field, A a k-algebra)  (
(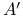 an A-algebra)
an A-algebra)  ,
,  , df(x) (f a morphism from X to Y,
, df(x) (f a morphism from X to Y,  ,
, 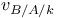 (A a k-algebra, B an A-algebra)
(A a k-algebra, B an A-algebra)  (F a Module)
(F a Module) ![$[A, Hom_k (M,N)]$](/math_tex/f2991245a7e1f504fefc48bb747324bf82.gif) (A a k-algebra, M, N A-modules)
(A a k-algebra, M, N A-modules) 
 ,
,  (M an A-module)
(M an A-module) 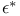
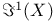 (X a locally noetherian scheme)
(X a locally noetherian scheme)  (F a locally free sheaf)
(F a locally free sheaf) 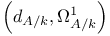 (A a k-algebra)
(A a k-algebra)  (
( a polynomial)
a polynomial)  (
( a protective system)
a protective system)  (X a Y-scheme)
(X a Y-scheme)  (N a filtered module)
(N a filtered module) 
 ,
, 

 , dim(M) (X a topological space , M an A-module)
, dim(M) (X a topological space , M an A-module)  (M a filtered A-module , q an ideal)
(M a filtered A-module , q an ideal)