Авторизация
Поиск по указателям
Dieudonne J. — Linear Algebra and Geometry.
Обсудите книгу на научном форуме Нашли опечатку?
Название: Linear Algebra and Geometry.Автор: Dieudonne J. Аннотация: This book gives a complete and detailed account of the basic ideas and theorems of elementary linear algebra which represent the very least a competent French "bachelier" should know when embarking upon the "propedeutique" courses. The general approach and content of the book were determined by the desire to prepare the student to assimilate as easily as possible, the actual teaching he is receiving at this time, which he should, in turn, regard as a natural extension of the work he has already been doing. At the moment, it is unlikely that one in a thousand students could cope with this book, unaided and without considerable hard work. This state of affairs says a great deal about the lack of cohesion in our teaching programmes. For years, teachers everywhere have expressed their concern about the everidening gap between the methods and attitudes to the teaching of Mathematics in the secondary schools on the one hand and in the universities on the other. Having participated in many discussions on this problem, I have succeeded in convincing myself that even among those secondary school teachers who are most keenly aware of the need for reform, there exists a great uncertainty about the content of new courses, their structure and their connection with the various courses in the university. So it is, in fact, for these people that this book is primarily intended. I have devised it as a "teacher's book"; in other words, its aim is to provide a solid framework upon which to base lively oral teaching adapted to those pupils for whom it is intended.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1969Количество страниц: 205Добавлена в каталог: 17.02.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Abelian group 1.2 Absolute quadric (in a non-Euclidean space) Ap. II no. Absolute value of a complex number 5.5.4 Absolute value of a real number 1.19 Absolute value of an endomorphism 5.2 Ex. Acute angle (positive or negative acute angle) 5.4.1.2 Acute sector 5.4.1.2 Addition of vectors 3.30 Adjoint endomorphism 5.2.5 7.1.5 Ap. no. Affine group 3.2.20 Affine half-line 3.3.3 Affine homothetic mapping 3.2.18 Affine hyperplane 3.3.5 Affine isometry 5.1.14 Affine line 3.3.1 Affine linear mapping, mapping 3.2.17 Affine quadric Ap. II no. Affine similitude 5.1.14 Alternating bilinear map 3.2.14 Alternating matrix 4.2.4 Alternating trilinear form 3.2.15 Angle (positive/negative acute angle) 5.4.1.2 Angle (positive/negative obtuse angle) 5.4.1.2 Angle (positive/negative right angle) 5.4.3 Angle (Right angle for lines) 5.4.14 Angle (straight angle) 5.4.1 Angle made by a pair of half-lines, of a pair of affine half-lines 5.4.6 Angle of a pair of concurrent non-Euclidean lines Ap. II no. 27 Angle of a pair of lines, a pair of half-lines 5.4.14 Angle of a pair of vectors 5.4.9 Angle of a rotation in a Euclidean plane 5.4.1 Angle of a rotation, angle of a pair of vectors in three-dimensional space 7.2.5 Angles (Right angles) 5.4.1 Antihermitian endomorphism 5.2.5 7.1.5 Antisymmetric bilinear map 3.2.14 Antisymmetric endomorphism 5.2.5 7.1.5 Antisymmetric matrix 4.2.4 Antisymmetric trilinear map 3.2.15 Arc of a sector 5.4.13 Argument of a complex number 5.5.5 Associated linear map (with a bilinear form) 5.2.4 7.4.5 Ap. no. Associated linear map of an affine map 3.2.17 Associated translation of an affine map 3.2.5 Automorphism of a vector space 3.2.8 Automorphism preserving the orientation (resp. reversing the orientation) 4.3.2 6.2.13 Axis of a rotation in three-dimensional space 7.2.3 Ball (open, closed), concentric balls 5.1.9 Ball (unit) 5.1.9 Basis (dual) 4.1.15 6.1.9 Ap. no. Basis (isotropic) Ap. II no. Basis (orthogonal/orthonormal) 5.2.1 7.1.1 Ap. no. Basis (positive orthonormal) 5.4.4 Basis of a vector space 4.1.2 6.1.1 Bilinear form, map 3.2.1.2 Bisector of a sector 5.4.13 Bisectors of a pair of lines 5.4.14 Bisectors of a pair of vector half-lines 5.4.8 Bruhat decomposition 4.1 Ex. 6.1 Ex. Cayley — Hamilton theorem 4.1 Ex. 6.2 Ex. Centre of a ball, sphere 5.1.9 Centre of a homothetic map 3.2.18 Centre of a ring, group 4.1 Ex. Centre of a rotation 5.3.6 Centre of a similitude 5.3.5 Change of basis 4.2.15 6.2.11 Change of origin 3.2.21 Characteristic equation/polynomial of an endomorphism 4.2.14 6.2.10 Characteristic subspace 3.2.10 Characteristic value of a symmetric bilinear form 5.2.7 7.1.6 Characteristic value of an endomorphism 3.2.10 Characteristic vector of an endomorphism 3.2.10 circle 5.2.3 Circles (paratactic) Ap. IV no. Clifford parallelism/translations Ap. IV no. Closed ball 5.1.9 Closed half-line 3.3.3 Closed half-space 3.3.7 Closed sector 4.3.8 Closed segment 3.3.4 column 4.2.11 6.1.8 Commutator (or derived) group 4.1 Ex. Complex conjugate 5.5.4 complex numbers 5.5.2 Concentric balls/spheres 5.5.2 Cone (Isotropic/light) Ap. II no. Conformal group Ap. III no. Conjugate complex numbers 5.5.4 Conjugate points with respect to a quadric Ap. II no. Conjugate quaternions Ap. IV no. Coordinate functions 4.1.15 6.1.9 coordinates 4.1.2 6.1.1 Coorthogonal degenerate spheres Ap. III no. Coorthogonal spheres 5.1 Ex. Cosine of an angle 5.4.3 Cotangent of an angle 5.4.5 Cramer's formulae 4.2.11 6.2.7 Decomposition (Bruhat) 4.1 Ex. 6.1 Ex. Decomposition (Direct decomposition of a vector space) 3.1.8 Decomposition (Iwasawa) 5.2 Ex. 7.1 Ex. Degenerate bilinear form 4.2 Ex. Ap. no. Degenerate sphere Ap. III no. Dependence (Linear) 4.1.1 Determinant 5.3.4 7.2.6 Determinant (Gramian) 7.1 Ex. Determinant of a matrix 4.2.9 6.2.5 Determinant of an endomorphism 4.2.6 6.2.4 Diagonal matrix 4.1 Ex. Diameter, diametral hyperplane 5.1.9 Diametrically opposite points 5.1.9 Dilation 3.3 Ex. Dimension of a vector space Ap. II no. Direct decomposition/sum 3.1.8 Direct pair 4.3.1 Direct similitude 5.3.1 5.3.4 7.2.1 7.2.6 Ap. no. Direct sum of two orientations 6.2.14 Direct triplet 6.2.12 Direct triplet of half-lines 4.3.4 Direction of a half-line 3.3.3 Direction of a linear variety 3.1.12 Direction vector of a half-line 3.3.3 Direction vector of a line 3.3.1 Disc 5.2.3 Discriminant of a bilinear form 3.1.12 Distance (non-Euclidean distance) Ap. II no. 27 Distance between two parallel lines/parallel hyperplanes 5.1.8 Distance between two points 5.1.1 Distance of a point from a line/a hyperplane 5.1.7 5.1.8 Division ring Ap. IV no. Divisors of zero 4.1 Ex. Dual basis 4.1.15 Dual of a vector space 4.1.15 6.1.9 Ap. no. Eliptic non-Euclidean geometry Ap. II no. Endomorphism (adjoint of on endomorphism) 5.2.5 7.1.5 Ap. no. Endomorphism (antihermitian, antisymmetric, hermitian, self-adjoint, skew-symmetric, symmetric endomorphism) 5.2.5 7.1.5 Ap. no. Endomorphism (involutory endomorphism) 3.2.11 Endomorphism (nilpotent endomorphism) 4.1 Ex. Endomorphism (positive self-adjoint, positive hermitian endomorphism) 5.2 Ex. Endomorphism associated with a bilinear form 5.2.4 7.1.5 Endomorphism of a vector space 3.2.1 Endomorphisms (commuting endomorphism) 3.2 Ex. Equation (characteristic equation of an endomorphism) 4.2.14 6.2.10 Equation (homogeneous linear equation) 4.2.13 Equation of a hyperplane 3.3.6 Equivalent bilinear forms 4.2 Ex. Euclidean n-dimensional space Ap. II no. Euclidean plane/two-dimensional space 3.1 Euclidean space 50 Euclidean three-dimensional space 2.2 Exterior of a ball 5.1.9 Extremities of a sector 4.3.5 4.3.8 Extremities of a segment 3.3.4 Field of complex numbers 5.5.2 Field of quaternions Ap. IV no. Flag 6.1 Ex. Form (bilinear form) 3.2.12 Form (degenerate bilinear form) 4.2 Ex. Ap. no. Form (linear form) 3.2.1 Form (non-degenerate positive/negative symmetric bilinear form) 50 Ap. no. Form (positive definite bilinear form) 50 Form (trilinear form) 3.2.15 Forms (equivalent bilinear forms) 4.2 Ex. Gauchy — Schwarz inequality 5.1.2 Gayley's parametric representation 5.5 Ex. 7.2 Ex. Gentralizer of a subset of a group 4.1 Ex. Geometry (Euclidean geometry of n dimensions) Ap. II no. Geometry (non Euclidean hyperbolic geometry) Ap. II no. Geometry (non-Euclidean elliptic geometry) Ap. II no. Gramian matrix, determinant 7.1 Ex. Grassmann's relation Ap. II no. Greater of two real numbers 1.11 Group (affine group) 3.2.20 Group (conformal group) Ap. III no. Group (derived group) 4.1 Ex. Group (linear group) 3.2.8 Group (Lorentz group) Ap. II no. Group (multiplicative group of real numbers 1.5 Group (orthogonal group) 5.1.12 Ap. no. Group (projective group) Ap. II no. Group (Unimodular group) 4.2 Ex. 6.2 Ex. Group of affine isometries 5.1.14 Group of affine similitudes 5.1.14 Group of angles for half-lines 5.4.1 Group of angles for lines 5.4.14 Group of direct displacements 5.3.4 7.2.6 Group of direct similitudes 5.3.1 7.2.1 Group of linear isometries 5.1.12 Group of linear similitudes (or similitudes) 5.1.12 Group of orthochrone rotations Ap. II no. 20 Group of rotations 5.3.1 7.2.1 Ap. no. Group of translations and homothetic maps 3.3 Group preserving an orientation 4.3.1 6.2.13 Group with triply transitive action 4.1 Ex. Helicoidal displacement 7.2 Ex. Hermitian endomorphism 5.2.5 7.1.5 Ap. no. Hermitian endomorphism (positive) 5.2 Ex. 7.2 Ex. Homogeneous linear equation 4.2.13 Homothetic mapping, affine homothetic mapping 3.2.8 Homothetic mapping, linear homothetic mapping 3.2.2 Hyperbolic non-euclidean geometry Ap. II no. Hyperbolic plane Ap. II no. Hyperplane (diametral hyperplane of a sphere) 5.1.9 Hyperplane (fixed hyperplane of a dilation, transvection) 3.3 Ex. Hyperplane (points on either/same side of a hyperplane) 3.3.7 Hyperplane (polar hyperplane of a point w.r.t. a projective quadric) Ap. II no. Hyperplane (projective hyperplane) Ap. II no. Hyperplane (radical hyperplane of two spheres) 5.1 Ex. Hyperplane (vector hyperplane orthogonal to a vector line) 5.1.7 Ap. no. Hyperplane at infinity Ap. II no. Hyperplane normal to a line Ap. II no. 27 Hyperplane perpendicular to a line 5.1.8 Ap. no. 27 Hyperplane, (affine hyperplane, vector hyperplane) 3.3.5 Hyperquadric Ap. II no. Ideals in End(E) 4.1 Ex. Idempotent 3.2 Ex. Image of a linear mapping 3.2.3 Imaginary part of a complex number 5.3.3 Index of a symmetric bilinear form Ap. II no. Inequality (Gauchy — Schwarz inequality) 5.1.2 Inequality (Minkowski's inequality) 5.1.3 Inequality (Ptolemy's inequality) 5.1 Ex. Inequality (Triangular inequality) 5.1.3 Invariance of distance under translation 5.1.1 Inverse affine similitude 5.3.4 7.2.6 Inverse displacement 5.3.4 7.2.6 Inverse linear similitude 5.3.1 7.2.1 Ap. no. Inverse of non-zero real number 1.8 inversion Ap. III no. Inversion in a sphere Ap. III no. Invertible element of End(E) 3.2.8 Involution in GA(E) 3.2 Ex. Involution, involutory endomorphism 3.2.11 Isometry (affine isometry) 5.1.14 Isometry (linear isometry) 5.1.12 Isomorphic Euclidean spaces 5.1.12 Isomorphic vector spaces 3.2.5 Isomorphism (canonical isomorphism between a vector space and its bidual) Ap. II no. Isomorphism between Euclidean spaces 5.1.12 Isomorphism between vector spaces 3.2.5 Isotropic basis Ap. II no. Isotropic cone Ap. II no. Isotropic lines (vectors) Ap. II no. Isotropic subspace Ap. II no. Iwasawa decomposition 5.2 Ex. 7.1 Ex. Length of a vector, length of a segment 5.1.1 Lesser of two real numbers 1.11 Light cone Ap. II no. Line 4.1.11 6.1.8 Line (affine, vector line) 3.3.1 Line (dilation, transvection along a line) 3.3 Ex. Line (non-Euclidean line perpendicular to a line/hyperplane meeting it) Ap. II no. 27 Line (non-Euclidean line) Ap. II no. Line (projective line) Ap. II no. Line perpendicular to a hyperplane 5.1.8 Line with 0 removed 4.1.1 Linear (affine linear map) 3.2.17 Linear (affine linear variety) 3.1.10 Linear (projective linear map) Ap. II no. Linear (projective linear variety) Ap. II no. Linear form/functional 3.2.1 Linear group 3.2.8 Linear homothetic map 3.2.2 Linear mapping 3.2.1 Linear variety 3.1.10 Linearly dependent/independent sets 4.1.1 Lorentz group Ap. II no. Major sector 4.3.5 4.3.8 Mapping (affine linear mapping) 3.2.17 Mapping (affine mapping) 3.2.17 Mapping (alternating/antisymmetric/symmetric bilinear mapping) 3.2.14 Mapping (bilinear mapping) 3.2.14 Mapping (linear mapping associated with an affine mapping) 3.2.17 Mapping (linear mapping of rank 0, 1, 2, 3) 4.1.7 6.1.6 Mapping (linear mapping) 3.2.1 Mapping (p-linear mapping) 3.2.15 Mapping (projective linear mapping) Ap. II no. Mapping (quadratic mapping) 3.2 Ex. Mapping (trilinear/alternating trilinear/antisymmetric trilinear/symmetric trilinear mapping) 3.2.15 Mappings (linear mapping right- and left-associated with a bilinear form) 5.2.4 7.1.5 Ap. no. Matrix ( 4.1.12 Matrix ( 4.1.11 Matrix ( 6.1.8 Matrix (alternating, antisymmetric matrix) 4.2.8 Matrix (diagonal matrix) 4.1 Ex. 6.1 Ex. Matrix (Gram's) 7.1 Ex. Matrix (orthogonal matrix) 5.2.6 7.1.5 Matrix (permutation matrix) 6.1 Ex. Matrix (positive symmetric matrix) 5.2 Ex. 7.1 Ex. Matrix (scalar matrix) 4.1.13 6.1.8 Matrix (symmetric matrix) 4.2.4 6.2.3 Matrix (upper triangular matrix) 4.2.14 6.2.10 Matrix of a bilinear form 4.2.4 6.2.3 Matrix of a change of basis 4.2.15 6.2.11 Matrix of an endomorphism, linear functional, linear mapping, vector 4.2.11 6.1.8 Matrix of an endomorphism, of a linear mapping, of a linear form, of a vector 4.1.11 6.1.8 Matrix with three rows and three columns 6.1.8 Matrix with two rows and two columns 4.1.11 Maximal subgroup 4.1 Ex. Midpoint of a segment 3.3.4 Minkowski's inequality 5.1.3 Minor sector 4.3.5 4.3.8
Реклама
 |
|
О проекте
|
|
О проекте



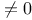 )
) 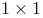 matrix)
matrix) 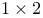 matrix,
matrix, 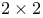 matrix,
matrix, 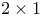 matrix)
matrix) 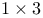 matrix,
matrix, 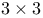 matrix,
matrix, 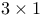 matrix,
matrix, 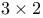 matrix,
matrix, 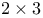 matrix)
matrix)