|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Koblitz N. — Introduction to Elliptic Curves and Modular Forms |
|
|
 |
| Предметный указатель |
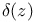 111—112 122 164 111—112 122 164
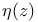 78 121 122 78 121 122
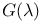 107 142 148 107 142 148
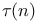 122 123 164 122 123 164
Addition law 7 29—35
Affine variety 52
Affine variety, coordinate ring of 55
Algebraic geometry 25—26
Algorithm for congruent number problem 4 5 222
Algorithm, semi-algorithm 5
Automorphy factor 148 152 153 177—178
Bernoulli numbers 110
Bernoulli polynomials 54
Bezout's theorem 32
Birch — Swinnerton — Dyer conjecture 3 46 90—93 218 221 222
Branch points 21 25
Character of group 61
Character, additive 57 62
Character, conductor 67
Character, Dirichlet 62 75
Character, multiplicative 57 62
Character, primitive 62
Character, quadratic 82 176 187—188 191—192
Character, trivial 57
Class number 176 194 218
Class number, relations 194
Coates — Wiles theorem 92 96 221
Coates, J. 92
Commensurable subgroups 165
Complex multiplication 42 50 92 124 143 222
Conductor of character 67
Conductor of elliptic curve 143
Congruence of elliptic curve 53 59
Congruence, principal 99
Congruence, subgroup 99—100
Congruence, zeta-function 51 52
Congruent number 1 3 5 46 70 92 221—222
Congruent Number Problem 1 2 4 221—222
Congruent number problem, generalized 8 123—124 223—224
Coordinate ring 55
Critical value 90 95 193 215 216 217
Cusp 103 106 108 126
Cusp, condition 125—126 180—182
Cusp, form 108 117—118 125 127 155 182
Cusp, irregular 144 182
Cusp, regular 144 174 182
Cyclotomic fields 37
Dedekind, eta-function 78 121 122
Dedekind, zeta-function 56 88 89
Deligne, P. 53 122 164
Diagonal hypersurface 56
Different 89
Dilogarithm 76 78
Diophantus 1
Dirichlet L-series 75 188 190 193
Dirichlet series 80 141
Dirichlet series and modular forms 140—143
Dirichlet theorem (primes in arithmetic progression) 45 142
Discriminant of polynomial 26
Discriminant, modular form 111—112 12 164
Double coset 165 204
Doubly periodic 14
Eigenforms for Hecke operators 163 173—174 201
Eigenforms for Hecke operators, Euler product 163
Eigenforms for Hecke operators, half integer weight 210—211 214
Eigenforms for Hecke operators, normalized 163
Eigenforms for involution of 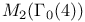 146 146
Eisenstein series 109—110 123 154 164 174 185
Eisenstein series of half integer weight 186—188 193
Eisenstein series of half integer weight, Euler product 199—201
Eisenstein series of level N 131—134
Eisenstein series, L-function of 146
Eisenstein series, normalized 111 122
Eisenstein, F. 177
Elementary divisor theorem 202
Elliptic curve 9 11
Elliptic curve over finite fields 40—41 43
Elliptic curve, addition law 7 29—35
Elliptic curve, additive degeneracy 36
Elliptic curve, complex multiplication 42 50 92 124 143 222
Elliptic curve, inflection points 13 35 41
Elliptic curve, Legendre form 224
Elliptic curve, multiplicative degeneracy 36
Elliptic curve, points of order 21 36 38—40
Elliptic curve, rank 44 46 51 91
Elliptic curve, torsion subgroup 36 43—44 49—50
Elliptic curve, Weierstrass form 24 26 33 120
Elliptic curve, Weierstrass form, functions 14—16 18 25
Elliptic curve, Weierstrass form, integrals 27—29 217
Elliptic curve, Weierstrass form, point 102 146
Euclid 1
Fermat 2 96
Fermat curve 56
Fermat last theorem 2 5
Fields of division points 37
Fields, cyclotomic 37
Fields, finite 40
Fourier transform 71 83
Fourier transform for finite group 76
Fractional linear transformation 98 102
Functional equation, Dedekind eta-function 78 121
Functional equation, Dedekind zeta-function 88 89
Functional equation, Dirichlet L-series 77—78
Functional equation, Hasse — Weil L-series 81 84 90 91
Functional equation, L-series of modular forms 140—143 216
Functional equation, Riemann zeta-function 73—74
Functional equation, theta-functions 73 76—78 85 88—89 124
Fundamental domain 100 103 105—107 146 231—232
Fundamental parallelogram 14
Galois action on division points 37—38 42 50
Gamma-function 70—71
Gauss lemma (on quadratic residues) 136
Gauss sums 56 62 67—68 188
Gaussian integers 14 41 42 65 165
General linear group 38 98
Genus 53—54
Good reduction 43 90
Grassmannian 55
Greenberg, R. 222
Gross, B.H. 93 222
Hardy, G.H. 177
Hass — Weil L-function 3 61 64 75 79 81 84 90 141
Hass — Weil L-function and modular forms 143
Hasse — Davenport relation 60 62—63 70
Hecke, E. 88 141 142
Hecke, E., character 81
Hecke, E., L-series 81
Hecke, E., operators 155 156 158 167 202
Hecke, E., operators, algebra of 157 210
| Hecke, E., operators, Euler product 158 160
Hecke, E., operators, Hermitian 168 172
Hecke, E., operators, in half integer weight 168 201 206—207 210
Hecke, E., operators, on q-expansion 161 163 207
Hecke, E., operators, trace 175
Hecke, E., operators, via double cosets 167 168 202
Heegner, K. 92—93
Homogeneous polynomial 10 12 52
Hurwitz, A. 194
Hypergeometric series 29
Irregular cusp 144 182
Isotropy subgroup 102
J-invariant 105 119—120 123—124
Jacobi, K. 112
Jacobi, K., forms 194
Jacobi, K., sums 56 57 61
Jacobi, K., triple product 219
Kohnen plus-subspace 213—214
Kohnen — Shimura isomorphism 201 213—216
Kohnen — Zagier theorem 216
Kohnen, W. 214
Kronecker, L. 194
L-function of modular form 140—143 216
L-function, Dirichlet 75 77—78 188 190 193
L-function, Hasse — Weil 3 61 64 75 79 81 84 90 141
Lattice 14 21 89 153
Lattice, dual 89
Legendre form of elliptic curve 224
Legendre symbol 60 65 82 136 147 178 187—188
Level 99
Line at infinity 10—11
Linear group, general 38 98
Linear group, special 98
Liouville's theorem 15
Mellin transform 71 84 85 139
Mellin transform, inverse 142
Modular curve 91
Modular form 96—97 108—109 117—118 125 127 155
Modular form and Dirichlet series 140—143
Modular form of half integer weight 3 176 178 182
Modular form with character 127 136—139 183
Modular form, Euler product 163
Modular form, weight one 165
Modular function 108 119 125 127 155 182
Modular group 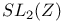 99 99
Modular point 153
Moebius function 188
Mordell theorem 43—44
Mordell — Weil theorem 44
Multiplicity One 173—174 214
New form 174
Niwa, S. 212 214 215
Pentagonal number theorem 123
Petersson scalar product 168 169—170 216
Points at infinity 10 11 13 103
Points at infinity on elliptic curve 11 12
Poisson summation 72 83
Projective completion of curve 11
Projective line 11 12 98 105
Projective plane 10
Projective plane, dual plane 12
Projective space 11
Projective variety 52
Pythagoras 1
Pythagorean triple 1—2 3 5 8
Pythagorean triple, primitive 5 6—7
q-expansion 104 109 125 126
Quadratic character 82 176 187—188 191—192
Quadratic form 176—177 221
Quadratic reciprocity 66 82 153
Quadratic residue symbol 60 65 82 136 147 178 187—188
Ramanujan conjecture 122 164
Ramanujan — Petersson conjecture 164
Ramanujan, 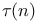 122 123 164 122 123 164
Ramanujan, S. 122
Ramification index 144
Rank of elliptic curve 44 46 51 91
Reduction mod p 43
Regular cusp 144 174 182
Representation 137 165
Representation, theory 215
Residue, field 43 55—56
Residue, theorem 15 30 116
Riemann sphere 10 21 98 105 119 120
Riemann surface 53 54 143
Riemann zeta-function 27 51 64 70 73
Root number 70 84 92 97
Shimura map 200—201 213—215
Shimura theorem 212—213 215
Shimura, G. 177 215
Shintani, T. 215
Smooth curve 9 13 52—53
Special linear group 98
Tangency, order of 13
Taniyama — Weil conjecture 91 143
Taniyama, Y. 91 143
Tate — Shafarevich group 218 222
Tate, J. 88
Theta-functions 72 76—78 84 88—89 96—97 124 176—177
Theta-functions, Hecke transformation formula 148
Torsion subgroup 36—37 43—44
Torus 14 15 21 24
Tunnell theorem 1 3 4 6 193 217 219—222
Tunnell, J. 1 200 217 219
Twisting 81 127 142 176
Type of finite abelian group 40
Upper half-plane 99
Variety, affine 52
Variety, projective 52
Waldspurger theorem 193 200 215 220
Waldspurger, J.-L. 215
Weierstrass 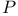 -function 16—18 21 134 -function 16—18 21 134
Weierstrass 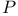 -function, derivatives of 17 18 20 21 22 -function, derivatives of 17 18 20 21 22
Weierstrass 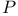 -function, differential equation of 21 22 24 -function, differential equation of 21 22 24
Weierstrass form of elliptic curve 24 26 33 120
Weight 108 153—154
Weight of polynomials 183
Weight, half integer 176
Weight, one 165
Weil Conjectures 53—54 91 122 139 164
Weil parametrization 91
Weil theorem 142—143 215
Weil — Taniyama conjecture 91
Weil, A. 44 91 141 142 143
Wiles, A. 92
Zagier, D. 93 194 222
Zeta-function, congruence 51 52
Zeta-function, Dedekind 56 88 89
Zeta-function, partial 132
Zeta-function, Riemann 27 51 64 70 73
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



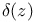
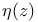
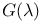
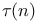
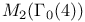
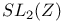
 -function
-function