|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kentaro Yano — Integral Formulas in Riemannian Geometry |
|
|
 |
| Предметный указатель |
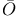 tsuki, T. 147 tsuki, T. 147
Absolute Betti number 117 133
Absolute value of a vector 2
Aeppli, A. 140
Affine collineation 24
Affine Killing vector field 24 35 36 44
Affine motion 24
Affine parameter 17
Affine vector field 24
Ako, M 114 115 116 118 122 124 149
Alexandrov, A. D. 140
Allendoerfer, C. B. 140
Angle between two vectors 2
Auslander, L. 1 140
Autoparallel curve 17
Ba, B. 122 140
Barbance, C. 49 140
Betti number 11
Bfanchi identity 13 31
Bishop, R. L. 1 54 62 140 141
Bochner, S. 1 39 42 44 71 75 76 77 117 120 124 141 150
Bochner’s lemma 39
Bonnesen, T. 141
Boothby, W. M. 141
Cartan, E. 1 141
Chern, S. S. 1 141
Christoffel three-index symbols 6
Codazzi, equation of 179 94 95
Codiflerential 10 64
Compact, I Complete 27
Complete Riemannian manifold 26
Condrcularly flat 176
conformal 27
Conformal Killing vector fields 26 37 46
Conformal Killing vector fields in Riemannian manifolds with boundary 120
Conformal motion 25
Conformal transformation 16 19 25
Conformal vector field 26
Conformally flat 21
Conjugate tensors 3
Conrircular curvature tensor 76
Contravariant components of the metric tensor 3
Couty, R. 46 142
Covariant components of the curvature tensor 13
Covariant components of the metric tensor 3
Covariant differentiation 6
Craig, H. V. 1 142
Crittenden, R. J. 1 140
Curvature and Betti numbers 70
Curvature and Killing tensor fields 73
Curvature tensor 11
de Rham, G. 127 147
Differential 9 63
Do Carmo, M. 141
Dual tensor 6
Duff, G. F. D 117 126 130 133 142
Eddington's epsilon 5
Ehresmann, C. 142
Einstein space 16
Eisenhart, L. P., I 32 142
Euler — Poincar characteristic 16 characteristic 16
Euler’s differential equations 6 29
Extension 88
Exterior differential 9
Fenchel, W. 141
Flanders, H. 1 142
Fundamental metric tensor 2
Gardner, R. 142
Gauss — Bonnet theorem 16
Gauss, equations of 79 91 92 94 95
Gaussian curvature 14
Geodesics 6
Gerretsen, J. C. H., I 142
Goldberg, S. I. 1 49 54 57 58 62 75 77 141 142 148
Gray, T. W. 143
Green's theorem 11
Guggenheimer, H. 1 143
Hardy, G. H 98 143
Harmonic 1-form 38 41
Harmonic 1-forms in Riemannian manifolds with boundary 113
Harmonic form 63 64
Harmonic forms in Riemannian manifolds with boundary 126 129
Harmonic tensor 10 64
Hatakeyama, Y. 143
Helgason, S. 1 143
Hicks, N. 1 143
Hilt, A, L. 143
Hodge, theorem of 11
Hodge, W, V. D. 1 10 11 143
Homothetic transformation 19
Hopf, E 143
Hopf, H 27 143
Hsiung, C. C. 49 58 114 118 122 126 130 143 144
Hypersurfaces of Euclidcan space 78
Hypersurfaces of Riemannian manifolds 78 100
Hypersurfaces with constant first mean curvature 109
Identity tensor 3
Induced connection 89
Inner product 3
Integral formulas 38
Integral formulas for the case 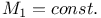 104 105 104 105
Integral formulas in 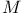 admitting a function admitting a function 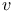 such that such that 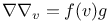 107 107
Ishihara, S. 28 144 150
Isometric 27
Isometry 23
K hler, E. 144 hler, E. 144
K jy jy , H. 100 144 , H. 100 144
Katsurada, Y 100 105 143 144
Killing tensor field 63 68
Killing tensor fields in Riemannian manifolds with boundary 116 134
Killing vector field 24 35 38 43
Killing vector fields in Riemannian manifolds with boundary 113 118
| Killing, W. 144
Killing’s equation 24
Kobayashi, S. 1 58 141 142 144
Kodaira, K. 10 147
Kostant, B. 145
Kot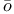 , S. 145 , S. 145
Koyanagi, T. 145
Kronecker delta 3
Kurita, M. 145
Lang, S., I 145
Laplacian 11
Laugwitz, D. 1 145
Ledger, A. J. 145
Length of a tensor 4
Length of a vector 2
Levi — Civita, T. 1 145
Lichnerowicz, A. 1 47 54 58 71 145
Lie derivative 21 22
Lie difference 22
Liebmann, H. 83 145
Littlewood, J. E. 98 143
Liu, J. D. 49 144
Locally Euclidean 12
Locally flat 12
Lowering of index 3
MacKenzie, R. 1 140
Matsushima, Y. 146
McConnell, A. J. 1 146
Mean curvature 81
Mogi, I. 77 146
Motion 23
Myers, S. B. 42 146
Nagai, T. 100 144 146
Nagano, T. 27 57 146 150
Nakae, T. 117 146
Newlander, A. 146
Nijenhuis, A. 146
Nirenburg, L. 146
Nomizu, K. 1 144 146
Nonexistence of harmonic  -forms 131 -forms 131
Nonexistence of Killing  -forms 136 -forms 136
Normal part 126
Obata, M. 28 49 54 62 145 146 150
Ogawa, Y. 147
Okumura, M. 100 147 150
Orientable 2
O’Neill, B. 1 147
Paths 17
Projective change 17
Projective collineation 24
Projective Killing vector field 25 36 45
Projective motion 24
Projective transformation 16
Projective vector field 25
Projectively flat 18
Projectively related 17
Raising of index 4
Relative Betti number 117 133
Ricci curvature 16
Ricci identity 12
Riemann — Christoffel curvature tensor 12
Riemannian connection 9
Riemannian geometry 1
Riemannian manifold 1 2
Rinow, W. 27 143
S ss, W. 83 148 ss, W. 83 148
Sasaki, S. 147
Sat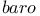 , I. 47 147 , I. 47 147
Sawaki, S. 147 150
Scalar curvature 14
Schild, A., I 148
Schouten, J. A. 1 92 147
Second fundamental tensor 79 90
Section 15
Sectional curvature 15
Shahin, J. K. 144 147
Simons, J. 147
Smyth, B. 146
Sokolnikoff, I. 1 147
Space of constant sectional curvature 15
Spain, B. 1 147
Spencer, D. C. 117 126 130 133 142
Springer, C. E. 1 147
Sternberg, S. 1 147
Stokes' theorem 113
Stong, D. J. 148
Struik, D. J. 1 148
Synge, J. L. 1 148
Tachibana, S. 148
Takahashi, T. 126 130 131 139 148 150
Tangential part 126
Tani, M. 87 100 148 150
Tashiro, Y. 28 144 148
Tazawa, Y. 148
Thomas, T. Y. 1 148
Totally geodesic 92
Totally umbilical 92
Trudinger, N. S. 21
van der Waerden — Bortolotti covariant derivative 91
Veblen, O. 1 148
Voss, K. 143 148
Wang, H. C. 141
Watanabe, Y 42 43 148
Weatherburn, C. E. 1 148
Weber, W. C., I 57 148
Weingarten, equation of 79 91 93
Weyl conformal curvature tensor 20
Weyl projective curvature tensor 18
Weyl, H 1 18 20 21 32 148
Willmore, T. J. 1 149
Woolf, W. B. 146
Yamabe, H. 21 149
Yano.K. 1 21 27 45 46 47 49 54 56 57 58 59 62 71 73 75 76 77 100 106 109 110 111 114 115 116 118 119 122 123 124 126 130 131 141 142 147 149 150
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



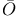 tsuki, T.
tsuki, T.  characteristic
characteristic 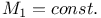
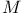 admitting a function
admitting a function 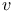 such that
such that 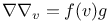
 hler, E.
hler, E.  jy
jy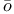 , S.
, S.  -forms
-forms  ss, W.
ss, W. 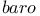 , I.
, I.