Williams D. — Probability with Martingales :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Williams D. — Probability with Martingales

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Probability with Martingales

Автор: Williams D.

Аннотация:

The author adopts the martingale theory as his main theme in this introduction to the modern theory of probability, which is, perhaps, at a practical level, one of the most useful mathematical theories ever devised.

Язык:

Рубрика: Математика/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Год издания: 1991

Количество страниц: 251

Добавлена в каталог: 03.03.2006

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

$\pi$ -system      (1.6)
$\pi$ -system, Uniqueness Lemmas      (1.6 4.2)
$\sigma$ -algebra      (1.1)
'extension of measures', existence      (1.7)
'extension of measures', uniqueness      (1.6)
A.N. KOLMOGOROV’s Definition of Conditional Expectation      (9.2)
A.N. KOLMOGOROV’s Inequality      (14.6)
A.N. KOLMOGOROV’s Law of the Iterated Logarithm      (A4.1 14.7)
A.N. KOLMOGOROV’s Strong Law of Large Numbers      (12.10 14.5)
A.N. KOLMOGOROV’s Three-Series Theorem      (12.5)
A.N. KOLMOGOROV’s Truncation Lemma      (12.9)
A.N. KOLMOGOROV’s Zero-One (0—1) Law      (4.11 14.3)
Abracadabra      (4.9 E10.6)
Adapted process      (10.2)
Adapted process, Doob decomposition      (12.11)
Algebra of sets      (1.1)
Almost everywhere = a.e.      (1.5)
Almost surely = a.s.      (2.4)
Atoms of $\sigma$ -algebra      (9.1 14.13)
Atoms of distribution function      (16.5)
Azuma — Hoeffding inequality      (E14.2)
Baire category theorem      (A1.12)
Banach — Tarski paradox      (1.0)
Bayes' formula      (15.7—15.9)
Bellman optimality principle      (E10.2 15.3)
Black — Scholes option-pricing formula      (15.2)
Blackwell’s Markov chain      (E4.8)
Bochner’s theorem      (E16.5)
Borel — Cantelli Lemmas, First = BC1      (2.7)
Borel — Cantelli Lemmas, Levy’s extension of      (12.15)
Borel — Cantelli Lemmas, Second = BC2      (4.3)
Bounded Convergence Theorem = BDD      (6.2 13.6)
Branching process      (Chapter 0 E12.1)
Burkholder — Davis — Gundy inequality      (14.18)
Caratheodory’s Lemma      (A1.7)
Caratheodory’s Theorem, proof      (A1.8)
Caratheodory’s Theorem, statement      (1.7)
Central limit theorem      (18.4)
Cesaro’s Lemma      (12.6)
Characteristic functions, convergence theorem      (18.1)
Characteristic functions, definition      (16.1)
Characteristic functions, inversion formula      (16.6)
Chebyshev's inequality      (7.3)
coin tossing      (3.7)
Conditional expectation      (Chapter 9)
Conditional expectation, properties      (9.7)
Conditional probability      (9.9)
Consistency of Likelihood-Ratio Test      (14.17)
Contraction property of conditional expectation      (9.7
Convergence in probability      (13.5 A13.2)
Convergence theorems for integrals, BDD      (6.2 13.6)
Convergence theorems for integrals, DOM      (5.9)
Convergence theorems for integrals, Fatou      (5.4)
Convergence theorems for integrals, for UI RVs      (13.7)
Convergence theorems for integrals, MON      (5.3)
Convergence theorems for martingales, Downward      (14.4)
Convergence theorems for martingales, for UI case      (14.1)
Convergence theorems for martingales, Main      (11.5)
Convergence theorems for martingales, Upward      (14.2)
d-system      (A1.2)
Differentiation under integral sign      (A16.1)
Distribution function for RV      (3.10—3.11)
Dominated Convergence Theorem = DOM      (5.9)
Dominated Convergence Theorem = DOM, conditional      (9.7
Downward Theorem      (14.4)
Dynkin’s Lemma      (A1.3)
Events      (Chapter 2)
Events, independent      (4.1)
Expectation      (6.1)
Expectation, conditional      (Chapter 9)
Extinction probability      (0.4)
Fair game      (10.5)
Fair game, unfavourable      (E4.7)
Fatou Lemmas for functions      (5.4)
Fatou Lemmas for sets      (2.6 2.7
Fatou Lemmas, conditional version      (9.7
Filtered space, filtration      (10.1)
Filtering      (15.6—15.9)
Finite and $\sigma$ -finite measures      (1.5)
Forward Convergence Theorem for supermartingales      (11.5)
Fubini’s Theorem      (8.2)
Gambler’s ruin      (E10.7)
Gambling strategy      (10.6)
Hardy space 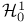$\mathcal{H}_{0}^{1}$       (14.18)
harnesses      (15.10—15.12)
Hedging strategy      (15.2)
Helly — Bray lemma      (17.4)
Hitting times      (10.12)
Hoeffding’s Inequality      (E14.2)
Hoelder’s inequality      (6.13)
Hunt’s Lemma      (E14.1)
Independence and product measure      (8.4)
Independence, $\pi$ -system criterion      (4.2)
Independence, and conditioning      (9.7 9.10)
Independence, definitions      (4.1)
Inequalities, Azuma — Hoeffding      (E14.2)
Inequalities, Burkholder — Davis — Gundy      (14.18)
Inequalities, Chebyshev      (7.3)
Inequalities, Doob’s 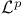$\mathcal{L}^{p}$       (14.11)
Inequalities, Hoelder      (6.13)
Inequalities, Jensen      (6.6)
Inequalities, Jensen, and in conditional form      (9.7
Inequalities, Khinchine - see      (14.8)
Inequalities, Kolmogorov      (14.6)

Inequalities, Markov      (6.4)
Inequalities, Minkowski      (6.14)
Inequalities, Schwarz      (6.8)
Infinite products of probability measures      (8.7 Chapter
Infinite products of probability measures, Kakutani’s Theorem on      (14.12 14.17)
Integration      (Chapter 5)
J.L. DOOB’s Convergence Theorem      (11.5)
J.L. DOOB’s Convergence Theorem, 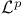$\mathcal{L}^{p}$ inequality      (14.11)
J.L. DOOB’s Convergence Theorem, Decomposition      (12.11)
J.L. DOOB’s Convergence Theorem, Optional Sampling Theorem      (A14.3—14.4)
J.L. DOOB’s Convergence Theorem, Optional Stopping Theorem      (10.10 A14.3)
J.L. DOOB’s Convergence Theorem, Submartingale Inequality      (14.6)
J.L. DOOB’s Convergence Theorem, Upcrossing Lemma      (11.2)
Jensen’s Inequality      (6.6)
Jensen’s inequality, conditional form      (9.7
Kakutani’s Theorem on likelihood ratios      (14.12 14.17)
Kalman — Bucy filter      (15.6—15.9)
Kronecker’s lemma      (12.7)
Laplace transforms, and weak convergence      (E18.7)
Laplace transforms, inversion      (E7.1)
Law of random variable      (3.9)
Law of random variable, joint laws      (8.3)
Least-squares-best predictor      (9.4)
Lebesgue integral      (Chapter 5)
Lebesgue measure = Leb      (1.8 A1.9)
Lebesgue spaces 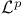$\mathcal{L}^{p}$ , $L^{p}$       (6.10)
Likelihood-Ratio Test, consistency of      (14.17)
Mabinogion sheep      (15.3—15.5)
Markov chain      (4.8 10.13)
Markov’s inequality      (6.4)
Martingale      (Chapters 10—15!)
Martingale transform      (10.6)
Martingale, convergence theorem      (11.5)
Martingale, definition      (10.3)
Martingale, Optional-Sampling Theorem      (Chapter A14)
Martingale, Optional-Stopping Theorem      (10.9—10.10 A14.3)
Measurable function      (3.1)
Measurable space      (1.1)
Measure space      (1.4)
Minkowski’s inequality      (6.14)
Moment problem      (E18.6)
Monkey typing Shakespeare      (4.9)
Monotone-Class Theorem      (3.14 A1.3)
Monotone-Convergence Theorem for functions      (5.3 Chapter
Monotone-Convergence Theorem for sets      (1.10)
Monotone-Convergence Theorem, conditional version      (9.7
Narrow convergence      see "Weak convergence"
Option pricing      (15.2)
Optional time      (10.8) see
Optional-Sampling Theorem      (Chapter A14)
Optional-Stopping Theorems      (10.9—10.10 A14.3)
Orthogonal projection      (6.11)
Orthogonal projection and conditional expectation      (9.4—9.5)
Outer measures      (A1.6)
P.LEVY’s Convergence Theorem for CFs      (18.1)
P.LEVY’s Downward Theorem for martingales      (14.4)
P.LEVY’s Extension of Borel — Cantelli Lemmas      (12.15)
P.LEVY’s Inversion formula for CFs      (16.6)
P.LEVY’s Upward Theorem for martingales      (14.2)
Polya’s urn      (E10.1 E10.8)
Previsible (= predictable) process      (10.6)
Probability density function = pdf      (6.12)
Probability density function = pdf, joint      (8.3)
Probability measure      (1.5)
Probability triple      (2.1)
Product measures      (Chapter 8)
Pythagoras’s theorem      (6.9)
Radon — Nikodym theorem      (5.14 14.13—14.14)
Random signs      (12.3)
Random walk, hitting times      (10.12 E10.7)
Random walk, on free group      (EG.3—EG.4)
Record Problem      (E4.3 E12.2 18.5)
Regular conditional probability      (9.9)
Riemann integral      (5.3)
Sample path      (4.8)
Sample point      (2.1)
Sample space      (2.1)
Schwarz inequality      (6.8)
Star Trek problems      (E10.10 E10.11 E12.3)
Stopped process      (10.9)
Stopping times      (10.8)
Stopping times, associated $\sigma$ -algebras      (A14.1)
Strassen’s Law of the Iterated Logarithm      (A4.2)
Strong Laws      (7.2 12.10 12.14 14.5)
Submartingales and supermartingales, convergence theorem      (11.5)
Submartingales and supermartingales, definitions      (10.3)
Submartingales and supermartingales, optional sampling      (A14.4)
Submartingales and supermartingales, optional stopping      (10.9—10.10)
Superharmonic functions for Markov chains      (10.13)
Symmetrization technique      (12.4)
Tail $\sigma$ -algebra      (4.10—4.12 14.3)
Tchebycheff = Chebyshev      (7.3)
Three-series theorem      (12.5)
Tightness      (17.5)
Tower property      (9.7
Truncation Lemma      (12.9)
Uniform integrability      (Chapter 13)
Uniqueness lemma      (1.6)
Upcrossing lemma      (11.1—11.2)
Weak convergence      (Chapter 17)
Weak convergence and characteristic functions      (18.1)
Weak convergence and Laplace transforms      (E18.7)
Weak convergence and moments      (E18.3—18.4)
Weierstrass approximation theorem      (7.4)
Zero-one law = 0—1 law      (4.11 14.3)

О проекте