|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Simmons G.F. — Introduction to topology and modern analysis |
|
|
 |
| Предметный указатель |
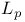 space 215 space 215
 -net 123 -net 123
Absolute value, of a function 159
Absolute value, on complex plane 53
Absolute value, on real line 52
Achieser, N.I. 157
Adjoint operation (involution), on 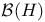 265 265
Adjoint operation (involution), on Banach *-algebra 324
Adjoint, of element in Banach *-algebra 324
Adjoint, of operator 263
Alexandroff, P. 130n
Algebra 106 208
Algebra B* 324
Algebra Banach 302
Algebra Banach* 324
Algebra Boolean see “Boolean algebra”
Algebra center 210
Algebra commutative 106
Algebra complex 106
Algebra disc 303
Algebra division 208
Algebra group 303—305
Algebra homomorphism 210
Algebra ideal in 209 313
Algebra isomorphism 210
Algebra quotient algebra of 209
Algebra radical 314
Algebra regular representation 210
Algebra semi-simple 316
Algebra subalgebra of 106 208
Algebra total matrix 284
Algebra von Neumann 303
Algebra W*- 303
Algebra with identity 106
Antisymmetry 43
Arzela's theorem 123
Ascoli's theorem 126 128
Axiom of Choice 46
B*-algebra 324
B*-algebra representation 325—326
Baire's theorem 74 75n
Banach *-algebra 324
Banach *-algebra, *-isomorphism 324
Banach algebra 302
Banach algebra, Banach subalgebra of 302
Banach algebra, representation 305
Banach space 82 212
Banach space, closed unit sphere 217 232
Banach space, representation 234
Banach space, uniformly convex 248
Banach — Steinhaus theorem 240
Banach — Stone Theorem 330
Bar-Hillel, Y. 7 46n
Base, closed 112
Base, generated by subbase 101 112
Base, open 99
Basis 197
Basis, orthonormal 293
Bell, E.T. 37
Bernstein polynomials 154
Bers, L. 338
Bessel's inequality 252—253 257
Birkhoff, G. 29 46n 47
Birkhoff, G.D. 338
Bolzano — Weierstrass property 21
Bolzano — Weierstrass theorem 121
Boolean algebra 345
Boolean algebra as Boolean ring 347—349
Boolean algebra, isomorphism 353
Boolean algebra, of sets 12 344
Boolean algebra, representation 353
Boolean ring 346
Boolean ring as Boolean algebra 348—349
Boolean ring as field 349—350
Boolean ring, maximal ideals in 350
Boolean ring, representation 351
Boolean ring, semi-simplicity 350
Boundary 68 97
Boundary point 68 97
Bounded function 55
Bounded linear transformation 220
Bounded mapping 58
Bounded set 58
Brouwer's fixed point theorem 338
C*-algebra 303
C*-algebra, commutative 332—334
Canonical form problem for matrices 286
Cantor continuum hypothesis 39
Cantor intersection theorem 73
Cantor set 67
Cantor, G. 31—43 49
Cardinal number(s) 31
Cardinal number(s) comparability theorem 48
Cardinal number(s) finite 32
Cardinal number(s) of continuum 39
Cartesian product (product of sets) 23—25
Cauchy sequence 71
Cauchy's inequality 88 219
Cayley's theorem 181
Chain 44
Characteristic equation 288-289
Characteristic value 278n
Characteristic vector 278n
Choice, axiom of 46
class 4
Class disjoint 9
Clelfand representation theorem 322
Closed base 112
Closed base, generated by closed subbase 112
Closed graph theorem 238
Closed mapping 342
Closed rectangle 101 119
Closed set 65 95
Closed sphere 66
Closed strips 101
Closed subbase 112
Closed unit sphere 217 232
Closure 58
Compact subspace 111
Compact topological space 110 111
Compactification, one-point 163
Compactification, Stone — Cech 141 331
Comparability theorem for cardinal numbers 48
Comparable elements 7 44
Complete metric space 71
Complete orthonormal set 255
Completely regular space 133
Completion of metric space 84—85
Complex plane 23 52—54
Complex plane extended 162
Component of a space 146
Congruent modulo, a linear subspace 193
Congruent modulo, a positive integer 30
Congruent modulo, an ideal 186
Conjugate space 224
Conjugate, of a function 108 161
Conjugate, of operator 241
Connected space 142 143
Connected subspace 143
continuous curve 341—342
Continuous function 50
Continuous image 93
Continuous linear functional 224
Continuous linear transformation 219 220
Continuous mapping 76 93
Continuous mapping at point 75-76 104
Continuous mapping in single variable 118
Continuous mapping jointly 118
Continuum, cardinal number 39
Continuum, hypothesis 39
| Contraction 338
Convergence of functions, point wise 83
Convergence of functions, uniform 83
Convergent sequence, in a space 70 132
Convergent sequence, limit 50 71 132
Convergent sequence, of numbers 50
Convex set 148
Convolution 304—305
Coordinate plane 22
cosets 186—187 193—194
Countably compact space 114
Courant, R. 94 338
Curve, continuous 341—342
Dense (everywhere dense) set 70 96
Derived set 96
Determinant, of matrix 287
Determinant, of operator 288
Dimension orthogonal, of a Hilbert space 259—260
Dimension, of a linear space 200
Disc algebra 303
Disconnected space 143
Disconnection of a space 143
Discrete space 93
Discrete topology 93
Discrete two-point space 144
Disjoint linear subspaces 195
Disjoint sets 9
Distance between two points 51
Distance, from point to set 58
Distributive laws, for lattices 345
Distributive laws, for sets 10
Division algebra 208
Divisor of zero 183
Divisor of zero topological 307
Dixmier, J. 303n
Dunford, N. ix 226 232n
Eigenspace 278
Eigenvalue 278
Eigenvector 278
Element(s) 3
Element(s) comparable 7 44
Element(s) in ring, regular 183 314
Element(s) in ring, singular 183 314
Element(s) maximal 44
Empty set 5
Equicontinuous functions 126
Equivalence relation 27
Equivalence set 27
Euclidean plane 22 87—88
Euclidean space, infinite-dimensional 90
Euclidean space, n-dimensional 24 87 214
Everywhere dense set 70 96
Extended complex plane 162
Extended real number system 56
Family 4
Field 184
Finite intersection property 47 112
First countable space 100n
Fixed point 338
Fixed point space 337—338
Fixed point theorem, Brouwer's 338
Fixed point theorem, Schauder's 338
Fomin, S.V. 128 215n
Fourier coefficients 256 257
Fourier expansion 256 257
Fraenkel, A.A. 7 42n 46n
Full linear group 207
Function spaces 82
Function(s), absolute value 159
Function(s), bounded 55
Function(s), complex 17
Function(s), conjugate 108 161
Function(s), constant 16
Function(s), continuous 50
Function(s), continuous at point 50
Function(s), convergence, pointwise 83
Function(s), convergence, uniform 83
Function(s), definition 16
Function(s), domain 15 16
Function(s), equicontinuous 126
Function(s), extension 17
Function(s), generalities 14—16
Function(s), imaginary part 161
Function(s), in contrast to mapping 17
Function(s), moments 157
Function(s), range 15 16
Function(s), real 17
Function(s), real part 161
Function(s), restriction 17
Function(s), uniformly bounded see also “Mapping” 128n
Function(s), vanishing at infinity 165
Functional(s) 224
Functional(s) extension 226—228
Functional(s) induced 231
Functional(s) multiplicative 321
Functional(s) on Hilbert space, representation 261
Fundamental theorem of algebra 245 289 310
Gal, I.S. 240
Galileo 33
Gelfand mapping 319
Gelfand — Neumark theorems 318 325—326
Godol, K. 39n
Goffman, C. 128
Goldberg, R.R. 305n
Gram — Schmidt process 258 295
Graph of mapping 23
Group 172—173
Group Abelian (commutative) 173 179
Group Abelian (commutative) additive 179
Group algebra 303—305
Group, abstract vs. concrete 173n
Group, center of 180
Group, circle 174
Group, finite 173
Group, full linear 207
Group, homomorphism 180
Group, identity in 173 179
Group, infinite 173
Group, inverses 173 179
Group, isomorphic 180
Group, isomorphism 180
Group, of symmetries of square 176—177
Group, order 173
Group, permutation 17
Group, regular representation 181
Group, subgroup of 178
Group, symmetric 176
Group, transformation 178 181
Hahn — Banach theorem 21 228
Hahn — Banach theorem, generalized form 230—231
Hahn — Mazurkiewicz Theorem 343
Hahn, H. 343
Halmos, P.R. 42n 46n 172 215n
Hausdorff space 130
Heine — Borel theorem 110 114
Heine — Borel theorem converse 115
Heine — Borel theorem generalized 119
Hermifce functions 259
Hewitt, E. 121n
Hilbert cube 248
Hilbert space(s) 245
Hilbert space(s) among complex Banach spaces 248
Hilbert space(s) inner product 245
Hilbert space(s) orthogonal complements 249
Hilbert space(s) orthogonal dimension 259—260
Hilbert space(s) orthogonal subspaces 250
Hilbert space(s) orthogonal vectors 249
Hilbert space(s) orthonormal set 251
Hilbert space(s) orthonormal set complete 255
Hilbert space(s) parallelogram law 247
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



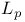 space
space  -net
-net