|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bini D., Pan V.Y. — Polynomial and matrix computations. Fundamental algorithms. Vol.1 |
|
|
 |
| Предметный указатель |
Machine precision 292
Mantissa 291
Markov parameters 155
Matrix algebra 134 186 209 215 216 220
Matrix block 92
Matrix determinant 86 96
Matrix diagonal 86
Matrix factorizations See factorization
Matrix generator 88 108
Matrix identity 86
Matrix inversion 87 96
Matrix kernel 89
Matrix multiplication 94
Matrix norms 90 124
Matrix operator 174—200 217
Matrix permutation 86
Matrix powers 97
Matrix rank 88 108
Matrix reversion 127
Matrix spectrum 87
Matrix tame 88 89 109 204
Matrix,  186—188 215 186—188 215
Matrix, adjugate (adjoint) 86
Matrix, anticirculant 132 215
Matrix, banded 208
Matrix, Bezout 155 156 310
Matrix, Cauchy 127 129
Matrix, Cauchy-like 180
Matrix, characteristic polynomial of a 87 96 190 316
Matrix, circulant 132—135 215
Matrix, companion 116
Matrix, condition number of a 91 124
Matrix, dense structured 81 82
Matrix, dense unstructured See general
Matrix, diagonally dominant 92 212
Matrix, down-shift 127
Matrix, eigenvalues 87 115
Matrix, f-circulant 132—135 181
Matrix, Fourier 12 128 220
Matrix, Frobenius 116 155 216 220
Matrix, general 81 332
Matrix, generalized Hubert 127 129 131
Matrix, generalized inverse 112
Matrix, generic 205
Matrix, h.n.d. 88
Matrix, h.p.d. 88
Matrix, Hankel 48 132 155
Matrix, Hankel-Like 180 337—350
Matrix, Hartley 216
Matrix, hermitian 88
Matrix, Hilbert-like 180
Matrix, irreducible 120
Matrix, Krylov 92 97
Matrix, Loewner 217
Matrix, lower triangular 86
Matrix, minimum polynomial of a 88 96
Matrix, nonderogatory 120
Matrix, nonsingular 87
Matrix, null 86
Matrix, null space of a 89 95 105
Matrix, orthogonal 86
Matrix, range 89
Matrix, real symmetric 88
Matrix, representation of Euclid's algorithm 147—149
Matrix, resultant 149
Matrix, similar 116
Matrix, singular 87
Matrix, sparse 81 118 172
Matrix, spectral radius 87
Matrix, strongly nonaingular 87 100 136 212
Matrix, structured See Dense structured
Matrix, subresultant 149
Matrix, Sylvester 149
Matrix, symmetric 88
Matrix, Toeplitz 132
Matrix, Toeplitz-like 180 191 337—350
Matrix, transposed 7
Matrix, transposed Vandermonde 63
Matrix, triangular 86
Matrix, tridiagonal 117 113 214
Matrix, unit triangular 86
Matrix, unitary 88
Matrix, upper triangular 86
Matrix, Vandennonde-like 180
Matrix, Vandermonde 127 128
Matrix-by-vector multiplication 94
Maximal linearly independent subset 109 368
MIN-POL 96 320 334
Minimum polynomial 88 96
Minimum span (of a recurrence) 47 140
MOD-POL-RECIPR 27 41
Model of computation 3 70—73
Modified (m, n) Hermite interpolation problem 45
Modular reduction 25
Modular, arithmetic 241
Modular, representation of a polynomial 27 31
Modular, rounding-off 241
Monte Carlo algorithms 5 72
Moore — Penrose generalized inverse 90 112 196 220
Multigrid 187 266—273 314
Multiplication of a vector by a Cauchy (Hilbert) matrix 261 312
Multiplication of a vector by a matrix 94
Multiplication of a vector by a transposed Vandermonde matrix 65 143
Multiplication of a vector by a Vandermonde matrix 128 312
Multiplication of a vector by the inverse of a Cauchy matrix 130 312
Multiplication of a vector by the inverse of a Hankel matrix 133
Multiplication of a vector by the inverse of a Toeplitz matrix 133
Multiplication of a vector by the inverse of a transposed Vandermonde matrix 143
Multiplication of a vector by the inverse of an f-circulant matrix 133
Multiplication of a vector by the inverse of Vandermonde matrix 128 312
Multiplication of integers 17
Multiplication of matrices 94
Multiplication of multivariate polynomials 61
Multiplication of several polynomials 12
Multiplication of two polynomials 13 23 56 277;
Multiplicity 32
Multivariate monomial 43
Multivariate polynomial 43 61—65
Multivariate polynomial interpolation 64
Multivariate polynomial multiplication 61
NC (class) 299
NC-algorithm 299
Newton — Henset's (p-adic) lifting 243 247 248
Newton's identities 34 141—144 163 212 330
Newton's iteration 18 22 49 68 147 189 265 283
Newton's polygon process 54
Newton's representation of a polynomial 67
Nonderogatory matrix 120
Nonsingular matrix 87
Normal equations 106
Normalization 291
Norms 90 124
Null space 59 95 105
NULL-SPACE 95 105 337
Numerical conditioning 233—237
Numerical Newton's iteration 24
Numerical stability 233—237
Numerical stabilization by means of equilibration 287
Numerically stable (algorithm) 234
Operator 174—200 217
Operator displacement 175
Operator norms 99
Operator of Cauchy (Hilbert) type 178
Operator of Hankel — Toeplitz type 175
Operator of Vandermonde type 180
OPS 7
Orthogonal Factorization 106 107
Orthogonal matrix 88
Orthogonal polynomials 136 137
Orthogonalization 121
| Outer product 278
Output sensitive 206 322
Output size 4
Overflow 292
Overhead constant 7
p-adic approximations 243
p-adic lifting 243 245 248
P-complete 300
pade 46 137
Pade approximation 46 138
Parallel cascade computation 306
Parallel RAM 6 296 304 305
Parallel time 7 73
PART-FRACT 30
Partial derivative 92
Partial differential equation 266
Partial fraction decomposition 30
Partial fraction expansion 260
Partial fractions 26
PDE 266
Permutation matrix 66
Pivoting 102 107
Pivoting, complete 102
Pivoting, partial 103
PLU-FACTORS 103
PLUP-FACTORS 102
POL-COMP 32 308
POL-DCOMP 52
POL-DIVIDE 18 20 22 307
POL-EVAL 9 25 67 307
POL-GCD 36
POL-INTERP 11 25 67 307
POL-LCM 39
POL-MODULI 27
POL-MULT 13 23 307
POL-RECIPR 22
POL-ROOT 51
POL-ZEROS 32
Polynomial approximate division with remainder 21
Polynomial composition 32
Polynomial decomposition 52
Polynomial division with remainder 18 20 22
Polynomial evaluation at a single point 8
Polynomial evaluation on a set of points 9 25
Polynomial gcd 36 42 47 147 150 151 155 161
Polynomial interpolation 11 25 277
Polynomial lcm 36 39 42 47 147 152 310
Polynomial multipucation 12 23 56 249—251 277
Polynomial multivariate 43 61—65
Polynomial reversion modulo 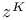 55 55
Polynomial sparse 64 65 257
Polynomial squaring 66
Polynomial, iterated product 12
Polynomial, modular representation 27
Polynomial, pseudo remainder sequence 41 153 238
Polynomial, reciprocal 22
Polynomial, reciprocal modulo m(x) 27 41
Polynomial, remainder sequence 41 238
Polynomial, reverse 34
Polynomial, root of a 51 55
Positive and/or negative wrapped convolution 13
Potential work 7
Power series 21 49 54
Power series composition 32
Power series correlation with polynomials 21
Power series multiplication 21
Power series over finite fields 312 313 372 375
Power series, generalized reversion 50
Power sums 33 34 69 372 375
PRAM 6 296 304 305
Preconditioned 135
Preconditioned conjugate gradient 187
Prefix computation 306
Primitive root of unity 9 69
Principal root of unity 11
Principal submatrix 86
Processor 6—7
Processor bound 296
Processor, efficient algorithm 299
Pseudo inverse 90
Pseudo regularity 268 269
Pseudo remainder sequence 41 153 238
Pseudo resultants 152
QR factorization with column pivoting 107
QR-FACTORS 107 319 321
QRP-FACTORS 107 319 321
Quadratic convergence 50
RAM (random access machine) 3 4
Randomization 42 47 53 60 71 72
Randomized algorithms 5 42—45 52 60 339—345
RANGE 89
Rank 88 108
Rank deficient matrix 88
RAT-INTERP 45
Rational algorithms 5 8 70
Rational arithmetic 241 242 247 289
Rational factorization 99 100 212
Rational functions 70
Rational interpolation 36 45
Rational interpolation table 46
Rational parallel triangulation 329
Rational restarting 302 303 365
Rational roundoff 247
Reciprocal of a polynomial 22 27
RECUR-SPAN 48 140 310
Recursive algorithms 9
Reducibility of problems 74—77 93 98 223—227
Refinement by integer rounding-off 252
Regularization 205—207
Regularization via randomization 60 201
Relative error 292
Repeated squaring 23
Representation error 292
Residual correction 262
Residue 19
Resultant matrix 149
Resultant polynomial 149
Reverse polynomial 34
Reversion matrix 127
Reversion of a polynomial modulo 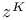 55 55
Rings 55 58 61 69
Rings, finite 17
Rings, mod N 55
Rokhlin's algorithms 257—262
Rounded value 291
Roundoff error 293
Roundoff integer 252
Roundoff rational 247
Sande — Tukey 123
Scaling procedure 207
Scaling the variable 16
Schoenhage — Strassen algorithm 17 78
Schur complement 99 100 168 169 212
SER-COMP 33 308
SER-MULT 21
SER-REVERSE 50 308
SEV-POL-CCD 42 151
SEV-POL-LCM 42 152
SEV-POL-MULT 112 307
Sherman — Morrison — Woodbury formula 89
Shift of the variable 15
Sieveking — Kung algorithm 22 24
Similarity transformation 116
Sine transform 66 215
Singular linear system 95
Singular matrix 87
Singular value decomposition (SVD) 89 124
Singular values 89
SINGULAR? 96
Size of the circuit 72
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте