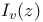|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Люк Ю. — Специальные математические функции и их аппроксимации |
|
|
 |
| Предметный указатель |
 -метод 529—533 -метод 529—533
E-функция Мак-Роберта 186
G-функция 163—271 312—333
G-функция, аналитическое продолжение 189—190
G-функция, представленная через специальные функции 327—331
G-функция, связь с 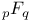 180—186 180—186
G-функция, элементарные свойства 186—189
Алгоритм Кленшо 511—515
Бета-преобразования для 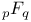 170—171 170—171
Бета-преобразования Эйлера 474
Биномиальный коэффициент 21—22
Вронскианы 2 86—287 310 335
Гамма-функции 11
Гамма-функции неполные 84—162 127 318
Гамма-функции неполные, вычисление 105—110
Гамма-функции, логарифмическая производная см. "Пси-функция"
Дельта-функция Кронекера 458
Дилогарифм 74
Доминанта 212
Интеграл Меллина — Барнса 180
Интеграл неопределенный для 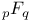 172 172
Интеграл от произведения двух G-функций 197—198
Интегралы неполные 443
Интегралы от бесселевых функций 337—338
Интегралы от многочленов Якоби 469
Интегралы полные 44
Интегралы полные эллиптические 319—320
Интегралы содержащие 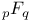 170—173 170—173
Интегралы содержащие G-функции 196—200
Интегралы Френеля 145—149
Интегральные представления для 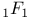 302—303 302—303
Интегральные представления для 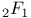 275 275
Интегральный косинус 122—126
Интегральный синус 122—127
Квадратный корень 36—38
Конфлюенция относительно  191 191
Коэффициенты ряда Якоби для функции, представленной рядом Тейлора 477—479
Коэффициенты ряда Якоби как интегральные преобразования 473—477
Коэффициенты Фурье 472
Математические константы 548—551
Метод выбранных точек 532—533
Метод основного ряда 546
Метод перевала 481 482
Метод суммирования регулярный 243
Многочлены Бернулли 242
Многочлены Бесселя 540—542
Многочлены Гегенбауэра 463
Многочлены Лежандра 463
Многочлены Лягерра 463
Многочлены Лягерра обобщенные 246
Многочлены ортогональные 319 457—515
Многочлены ультрасферические см. "Многочлены Гегенбауэра"
Многочлены Чебышева второго рода 463 489—490
Многочлены Чебышева второго рода сдвинутые 463 490—493
Многочлены Чебышева первого рода 457 463 484—490
Многочлены Чебышева первого рода сдвинутые 463 490—493
Многочлены Чебышева, ортогональность, суммируемость разложений 501—508
Многочлены Эрмита 464
Многочлены Якоби 463 466—484
Многочлены Якоби сдвинутые 463 467—468
Неравенства для 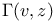 104 104
Неравенства для 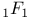 314 314
Неравенства для 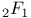 296 296
Неравенства для 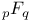 268—272 268—272
Неравенства для G-функции 268—272
Неравенства для H(v, z) 103—104
Неравенства для бесселевых функций 425—430
Неравенства для биномиальной функции 43—44
Неравенства для гамма-функций 26—29
Неравенства для гиперболических функций 68
Неравенства для логарифмических функций 50
Неравенства для обратных тригонометрических и гиперболических функций 79—80
Неравенства для показательной функции 59—60
Неравенства для функции ошибок 144—145
Оператор  542—544 542—544
Оператор d 542—544
Ортогональности соотношение 464
Повторные интегралы и производные от функции ошибок 129—130
Погрешность приближения к G-функции 245—247
Последовательность функций ортогональная 458
Последовательность функций ортонормированная 459
Правило трапеций 507
Предел конфлюентный 191
Преобразования H для G-функции 198
Преобразования K для G-функции 198
Преобразования Y для G-функции 198
Преобразования Ганнеля 475
Преобразования Ганнеля для G-функции 198
Преобразования квадратичные для 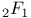 281 281
Преобразования Лапласа для 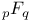 171 171
Преобразования Лапласа для G-функции 198—199
Преобразования Меллина для 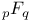 172 172
Преобразования Меллина для G-функции 196
Преобразования Фурье для G-функции 199—200
Преобразования Эйлера для G-функции 200
Приближение наилучшее чебышевское 524
Приближение Паде для 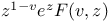 89—91 89—91
Приближение Паде для 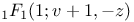 86—89 86—89
Приближение Паде для 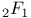 291—295 291—295
Приближение Паде для биномиальной функции 34—42
Приближение Паде для гиперболических функций 67—68
Приближение Паде для интегралов Френеля 146
Приближение Паде для интегральной показательной функции 118—122
Приближение Паде для квадратного и кубического корней 38—40
Приближение Паде для логарифмических функций 48—50
Приближение Паде для неполной гамма-функции 86—102
Приближение Паде для обратных гиперболических функций 77—78
Приближение Паде для обратных тригонометрических функций 75—76
Приближение Паде для показательной функции 55—59
Приближение Паде для функции ошибок 132—141
Приближение, наилучшее в смысле наименьших квадратов 459 524
Приближения Паде нормальные 528
Приближения Паде, оценка погрешности 40—42
Приближения полиномиальные 523—539
Приближения полиномиальные и рациональные для 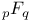 238—243 238—243
Приближения полиномиальные и рациональные для G-функций 243—247
Приближения рациональные 523—539
Приближения рациональные для 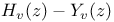 451—454 451—454
Приближения рациональные для 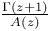 17 17
Приближения рациональные для интегральной показательной функции 113—117
Приближения рациональные для пси-функции 23—26
Приближения рациональные для тригонометрических функций 65—68
Приближения с помощью правила трапеций для функции ошибок 141—144
Приближения с помощью разложения Чебышева по многочленам первого рода 523—527
Приближения функций, определяемых дифференциальным уравнением см. " -метод" -метод"
Приближения функций, определяемых степенными рядами 533—534
Приближения экономизированные 529
Принцип конфлюентности 190—194
Произведения функций 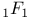 305 305
Произведения функций Бесселя 335—336
Производные от 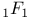 303 303
Производные от 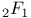 272—273 272—273
Пси-функция 11
Разложения 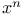 по многочленам Чебышева 488—489 492—493 по многочленам Чебышева 488—489 492—493
Разложения 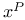 по многочленам Якоби 470—472 по многочленам Якоби 470—472
Разложения 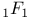 по многочленам Чебышева 312 по многочленам Чебышева 312
Разложения 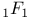 по функциям Бесселя 313 по функциям Бесселя 313
Разложения 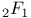 по многочленам Чебышева 291 по многочленам Чебышева 291
Разложения 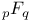 по многочленам Чебышева и обобщенным многочленам Якоби и Лягерра 233—237 по многочленам Чебышева и обобщенным многочленам Якоби и Лягерра 233—237
Разложения F(x) по многочленам Якоби 473—484
Разложения F(x) по многочленам Якоби сдвинутым 475
Разложения F(x) по многочленам Якоби, асимптотические оценки 479—484
Разложения G-функций по G-функциям 204—210
Разложения G-функций по многочленам Чебышева и обобщенным многочленам Якоби и Лягерра 225—233
Разложения асимптотические для G-функций 210—218
Разложения асимптотические для функций 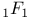 310—312 310—312
Разложения асимптотические для функций 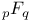 218—225 218—225
Разложения асимптотические для функций Бесселя 336—337
Разложения асимптотические для функций Ломмеля 444
Разложения асимптотические для функций Струве 444
| Разложения бесселевых функций по многочленам Чебышева 338—346 352—353 364—379
Разложения бесселевых функций по функциям Бесселя 382—383
Разложения биномиальной функции по многочленам Чебышева 33—34
Разложения биномиальной функции по многочленам Якоби 33—34
Разложения биномиальной функции по функциям Бесселя 34
Разложения гамма-функций и функций, с ней связанных 17
Разложения гамма-функций и функций, с ней связанных асимптотические 17—22
Разложения гиперболических функций по многочленам Чебышева 61
Разложения дилогарифма по многочленам Чебышева 74
Разложения интегралов бесселевых функций по многочленам Чебышева 347 354—358 380—381
Разложения интегралов Френеля по многочленам Чебышева 146—149
Разложения интегралов функций по многочленам Чебышева нечетного порядка 500
Разложения интегралов функций по многочленам Чебышева первого рода 493—500
Разложения интегралов функций по многочленам Чебышева первого рода сдвинутым 496—499
Разложения интегралов функций по многочленам Чебышева четного порядка 499—500
Разложения интегральных показательных функций по многочленам Чебышева 111—113
Разложения интегральных синуса и косинуса по многочленам Чебышева 123—126
Разложения конфлюентных гипергеометрических функций по многочленам Якоби 230
Разложения логарифмических функций по многочленам Чебышева 46—47
Разложения многочленов Чебышева по функциям 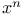 489—490 494—495 489—490 494—495
Разложения неполной гамма-функции 84—85
Разложения обратных гиперболических функций по многочленам Чебышева 70—75
Разложения обратных тригонометрических функций по многочленам Чебышева 70—75
Разложения показательной функции по бесселевым функциям 52—55
Разложения показательной функции по многочленам Чебышева и Якоби 52—55
Разложения рациональные для функций Бесселя 383—402
Разложения рациональные для функций Бесселя, большие значения 389—402
Разложения рациональные для функций Бесселя, малые значения 383—388
Разложения тригонометрических функций по многочленам Чебышева, Якоби и бесселевым функциям 60—65
Разложения функций Кельвина по многочленам Чебышева 359—363
Разложения функций Ломмеля по многочленам Чебышева и функциям Бесселя 444—450
Разложения функций Ломмеля по многочленам Якоби 230
Разложения функций ошибок по многочленам Чебышева и функциям Бесселя 130—132
Разложения функций Струве по многочленам Чебышева и функциям Бесселя 444—450
Решение дифференциальных уравнений разложением в ряд по многочленам Чебышева 534—539
Решение минимальное (антидоминантное) 516
Решение полное 307—308
Решения Куммера 278—279
Ряд базисный 477
Ряд гипергеометрический обобщенный 164
Ряд гипергеометрический усеченный 166
Ряд Фурье обобщенный 459
Ряды степенные для биномиальной функции 33
Ряды степенные для логарифмических функций 45—46
Ряды степенные для обратных гиперболических и тригонометрических функций 69—70
Ряды степенные для показательной функции 51
Ряды степенные для тригонометрических и гиперболических функций 60
Ряды степенные для функций 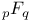 164—169 164—169
Ряды степенные для функций Бесселя 332—333
Ряды степенные для функций Ломмеля 442—444
Ряды степенные для функций Струве 442—444
Свойства ортогональности 458—465
Связь между функциями 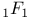 , U и Уиттекера 314—315 , U и Уиттекера 314—315
Скалярное произведение функций 458
Субдоминанта 212—213
Схема Горнера 508—515
Таблица Паде 527—529
Таблицы, вычисление и проверка 544—548
Теорема Вандермонда 288
Теорема о равносходимости 472
Теорема Спира 19
Теорема сходимости для приближений к 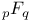 240 240
Теорема Уимпа 257
Теорема Цая 258
Теоремы асимптотических разложений для G-функций 211—212 214—218
Теоремы Корпута 18
Теоремы разложения для G-функций 208—210 225—230
Теоремы сходимости для приближений к G-функциям 244—245
Теоремы сходимости разложений по многочленам Якоби 472—473
Теоремы умножения для G-функций 194—196
Теоремы Филдса 191—194
Уравнения гипергеометрические, полное решение 280—286
Уравнения дифференциальные для G-функций 202—204
Уравнения дифференциальные для функций 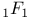 305—307 305—307
Уравнения дифференциальные для функций 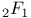 275—277 275—277
Уравнения дифференциальные для функций 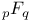 200—202 200—202
Уравнения неоднородные 520—522
Уравнения разностно-дифференциальные для многочленов Якоби 469
Уравнения разностно-дифференциальные функции Бесселя 334—335
Уравнения разностные однородные 516—520
Уравнения Шпигеля 290
Формула Ватсона 173
Формула Диксона 173
Формула дополнения для гамма-функций 21
Формула Зальшютца 173
Формула Парсеваля 460
Формула Родригеса 466
Формула трапеций 421 473
Формула Уиппла 173
Формулы дифференцирования гипергеометрических функций 169—170
Формулы для 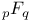 при частных значениях параметров и переменной 173—180 при частных значениях параметров и переменной 173—180
Формулы квадратурные для вычисления бесселевых функций 421—425
Формулы Кристоффеля — Дарбу 462
Формулы Куммера 307
Формулы рекуррентные для 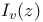 403—405 403—405
Формулы рекуррентные для 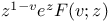 90 90
Формулы рекуррентные для 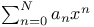 508—511 508—511
Формулы рекуррентные для 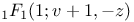 87 87
Формулы рекуррентные для 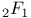 293 294 293 294
Формулы рекуррентные для 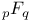 222—225 233—235 222—225 233—235
Формулы рекуррентные для G-функций 206 207 212 231—232
Формулы рекуррентные для бесселевых функций 403—421
Формулы рекуррентные для бесселевых функций погрешность 405—413
Формулы рекуррентные для биномиальной функции 36
Формулы рекуррентные для интегральной показательной функции 114
Формулы рекуррентные для обобщенных многочленов Якоби и Лягерра 249—258
Формулы рекуррентные для ортогональных многочленов 462
Формулы рекуррентные для пси-функции 23
Формулы рекуррентные для разложения G-функции по обобщенным многочленам Якоби 261—268
Формулы рекуррентные для рациональных приближений 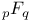 258—261 258—261
Формулы рекуррентные, вычисление по 516—522
Функции 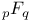 312—331 312—331
Функции Бесселя 320 332—456
Функции Бесселя ассоциированные 443
Функции Бесселя, представление через гипергеометрические функции 383—388
Функции Войгта 129
Функции гиперболические 60—68
Функции гиперболические обратные 69—80
Функции гиперболического типа 113
Функции интегральные показательные 110—123
Функции Кельвина 333
Функции Коломба волновые 320
Функции конфлюентные гипергеометрические смежные 304—305
Функции Лежандра 319
Функции логарифмические 45—51
Функции Ломмеля 442—45 6
Функции неполные 443
Функции смежные относительно 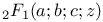 273—274 273—274
Функции специальные 312—331
Функции специальные, представленные через 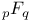 318—321 318—321
Функции специальные, представленные через G-функции 321—327
Функции Струве 442—456
Функции тригонометрические 60—68
Функции тригонометрические обратные 69—80
Функции Уиттекера 314 320
Функции цилиндрические 443
Функции Эйри 333—334
Функции элементарные 318
Функции Энгера — Вебера 442
Функция 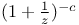 34—36 34—36
Функция 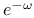 40—42 40—42
Функция 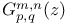 180 см. 180 см.
Функция 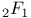 , аналитическое продолжение 279—280 , аналитическое продолжение 279—280
Функция 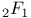 , частные случаи 287—290 , частные случаи 287—290
Функция Бесселя второго рода модифицированная 423—425
Функция Бесселя модифицированная 242
Функция Бесселя первого рода n-го порядка 422—423
Функция биномиальная 33—44
Функция гипергеометрическая Гаусса 272—301 318—319
Функция гипергеометрическая конфлюентная 191 302—317 320
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -метод
-метод 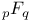
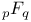
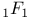
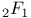

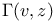

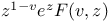
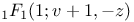
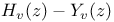
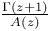
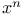 по многочленам Чебышева
по многочленам Чебышева 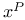 по многочленам Якоби
по многочленам Якоби