|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Грин Д., Кнут Д. — Математические методы анализа алгоритмов |
|
|
 |
| Предметный указатель |
Алгебраические особенности (algebraic singularities) 71—73
Амбле (Amble Ole) 111
Апостол (Apostol Tom Mike) 61 111
Асимптотический анализ (asymptotic analysis) 48—82 84—85 87—88 93—101 104—107
Ахо (Aho Alfred Vaino) 34 37 111
Банан (banana) 84
Бейли (Baily Wilfred Norman) 16 111
Бендер (Bender Edward Anton) 73 111
Бент (Bent Samuel Watkins) 7
Бета-функция (beta function) 107
Биномиальные тождества (binomial identities) 8—17
Бойс (Boyce William Edward) 22 111
Бродер (Broder Andrei) 7
Валле-Пуссен (de la Vallee Poussin Charles Louis Xavier Joseph) 66
Ватсон (Watson George Neville) 112
Виттер (Vitter Jeffrey Scott) 7
Гамма-функция (gamma function) 80
Гамма-функция метод (gamma function method) 107
Гармонические числа, асимптотики (harmonic numbers, asymptotics) 53 56
Гармонические числа, примеры (harmonic numbers, examples) 25—26 56 87
Гармонические числа, тождества (harmonic numbers, identities) 16—17
Гессель (Gessel Ira, M.) 10
Гипергеометрический ряд (hypergeometric series) 15—16
Голомб (Golomb Solomon Wolf) 35
Грамматика бесконтекстная (grammar, context free) 92
Грамматика однозначная (grammar, unambiguous) 92
Грин (Greene Daniel Hill) 3
Гульд (Gould Henry Wadsworth) 12 13
Гюиба (Guibas Leonidas Ioannis) 7
Дважды экспоненциальные последовательности (doubly exponential sequences) 33—37
Де Брейн (de Bruijn Nicolaas Govert) 32 50 52 100 111
Деланж (Delange Hubert) 29 111
Дерево бинарного поиска (tree, binary search) 85—87 88—89 102—104 107—109
Дерево бинарное сбалансированное (tree, balanced binary) 36
Дерево длина внешних путей (tree, external path length) 86—87
Дерево представление в виде бинарного дерева (tree, representing binary) 83—84 90
Дерево прохождение бинарного дерева (tree, traversing binary) 85 99—101
Дерево связанное в конце (tree, late binding) 85—87 88—89 102—104 107—109
Дерево суммарная длина путей (tree, total path length) 103
Дерево упорядоченное ориентированное (tree, ordered oriented) 31
Дзета-функция Римана (Riemann zeta function) 58 67—68
Ди Прима (DiPrima Richard Clyde) 111
Диагонализация ряда (diagonalization of series) 75 105
Дифференциальные уравнения (differential equations) 21 26 89 91 108
Драйсдейл (Drysdale Robert Lewis (Scot) III) 7
Дробь непрерывная (continued fraction) 31—33
Дробь подходящая (cenvergent fraction) 32
Дробь элементарная (partial fraction) 19—20 58
Егорычев Георгий Петрович 10
Егорычев метод коэффициентов (method of coefficients) 10—11
Золотое сечение (golden ratio) 36
Зэйв (Zave Derek Alan) 17 111
Индукция с другого конца (induction from the other end) 38 44—47 91
Интеграл контурный (contour integral) 70 74—76 78
Интеграл Стилтьеса (Stieltjes integral) 60—70
Интегральная показательная функция (exponential integral) 69
Информатика (Computer Science) 7
Иордан (Jordan Karoly) 18 111
Йонассен (Jonassen Arne Tormod) 9 111
Кларксон (Clarkson Kenneth Lee) 7 102
Кнут (Knuth Donald Ervin) 3—112
Конте (Comtet Louis) 73 112
Лидеры цикла (cycle leaders) 27
Люкер (Lueker George Schick) 21 112
Метод Дарбу (Darboux’s method) 70—73 76
Метод Лапласа (Laplace’s method) 76—80 82
Метод операторов (operator methods) 14—15
Метод перевала (saddle point method) 70 76—82
Метрика Ли (Lee metric) 1 06
Милн-Томсон (Milne-Thomson Louis Melville) 18 112
Минпозиция (minvolution) 30—31
Многочлены базисные (polynomials basic) 14—15
Многочлены Белла (polynomials Bell) 80
Многочлены Бернулли (polynomials Bernoulli) 54 65
Многочлены неприводимые (polynomials irreducible) 54
Множители простые необычные (factors prime unusual) 84 97—99
Множители простые различные (factors prime distinct) 66—70
Множители суммирующие (factors summation) 21 22 91
Монстр - пожиратель печенья (cookie monster) 38—47
Мэйрсон (Mairson Harry George) 7
Наибольший общий делитель (greatest common divisor) 77
Неопределенные коэффициенты (undetermined coefficients) 20
Неравенство Чебышева (Chebyshev’s inequality) 54
Неявные уравнения (implicit equations) 50
Обезьяна (ape) 84
Обращение Мёбиуса (Moebius inversion) 68
Ограниченная вариация (bounded variation) 62
Олвер (Olver Frank William John) 97 112
Операторы скользящие (sliding operators) 46—48 85 101—102
Операторы собственные (eigenoperators) 38—48
| Патерсон (Paterson Michael Stewart) 38—48
Пейдж (Page Ewan Stafford) 18 112
Перестановка (permutation) 86—88 102—104
Перестановка на том же месте (permutation in situ permutation) 27
Перестановка, получаемая с помощью стека (obtainable with a stack) 83
Перестановка, пузырьковая сортировка (bubble sort) 83 90
Перестановка, шейкер-сортировка (codail shaker) 83 90
Пласс (Plass Michael Frederick) 31
Постоянная Глейшера (Glaisher’s constant) 97
Постоянная Эйлера (Euler’s constant) 53 56
Правило Лопиталя (l’Hospital’s rule) 74
Принцип включения и исключения (inclusion and exclusion) 12
Принцип разделяй и властвуй (divide and conquer) 33
Произведение Адамара (Hadamard product) 76
Производящая функция (generating function) 10 13 19 21—22 26 31 38—48 70—82 83—84 89 90—93 99—100 102—104
Разбиение (partition) 54
Разложение Лорана (Laurent expansion) 71 74
Разложение на множители (factoring) 54—55
Разложение на множители различных степеней (factoring distinct degree) 54—55
Разложение Ньютона (Newton’s expansion) 15
Разложение Тейлора, обобщенное (Taylor’s expansion, general) 15
Разложение Тиле (Thiele expansion) 77—80
Райс (Rice Stepham Oswald) 32 111
Райт (Wright Edward Maitland) 33 68 113
Раскрутка (bootstrapping) 49 50 57 58 59
Расчленение суммы (dissecting a sum) 51 57—60
Рекуррентные соотношения линейные (recurrence relations linear) 18—27
Рекуррентные соотношения нелинейные (recurrence relations nonlinear) 27—37
Рекуррентные соотношения с полной предысторией (recurrence relations, full history) 18 23—27
Рекуррентные соотношения с частичной предысторией (recurrence relations, finite history) 18 18—23
Рекуррентные соотношения, вычитание (recurrence relations, differencing) 23
Реньи (Renyi Alfred) 113
Репертуарный подход (repertoire approach) 23—27 87
Решеточные пути (grid paths, lattice paths) 9 87 105 108
Рид (Read Rohald Cedric) 111
Риордан (Riordan John) 11 12 112
Рота (Rota Gian—Carlo) 14 15 112
Руссо (Rousseau Cecil Clyde) 10
Сдвиг среднего (shifting the mean) 81—82
Седгевик (Sedgewick Robert) 112
Семиинварианты (semi-invariants) 77 82
Символ C (O-notation) 49
Система 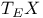 7 7
Система MACSYMA 93—97
Система METAFONT 7
Слейтер (Slater Lucy Joan) 16 112
Слияние последовательностей (merging sequences) 31
Слоан (Sloane Neal James Alexander) 34 37 111
Смышленый (Quick Jonathan Horatio) 85 88 104 109
Соотношения обратимые (inverse relations) 11—14
Соотношения обратимые чебышёвского типа (Chebyshev’s inverse relation) 12
Соотношения ортогональные (orthogonal relations) 11
Сортировка быстрая, вариант медиана из трех (median-of-three quicksort) 24
Сортировка поразрядная обменная (radix exchange sort) 14 106
Столарски (Stolarsky Kenneth Barry) 29 112
Столфи (Stolfi Jorge) 93
Суммирование по частям (summation by parts) 62 104
Суммирование, формула Эйлера (Euler’s summation formula) 54 60 64—65 93
Суммы цифр (digital sums) 29
Сю (Hsu Li-Che) 12 111
Таблица инверсий (inversion table) 90
Теорема абелева (Abelian theorem) 52
Теорема Вандермонда (Vandermonde’s theorem) 16
Теорема о вычетах (residue theorem) 74 78 100 105—107
Теорема тауберова (Tauberian theorem) 53 56 60
Теорема центральная предельная (central limit) 76—81
Траб Пардо (Trabb Pardo Luis Isidore) 70 112
Треугольник Паскаля (Pascal’s triangle) 89 108
Уилсон (Wilson Leslie Blackett) 18 112
Уинклер (Winkler Phyllis Astrid Benson) 7
Уиттекер (Whittaker, sir Edmund Taylor 112
Факториальные степени (factorial powers) 13—16
Фергюсон (Ferguson David Elton) 83—84
Формула Абеля — Плана (Abel — Plana formula) 97
Формула Стирлинга (Stirling’s approximation) 53 106
Формула суммирования Эйлера (Euler’s summation formula) 54 60 64—65 93
Фредмэн (Fredman Michael Lawrence) 30 112
Харди (Hardy Godfrey Harold) 33 53 68 112—113
Хенричи (Henrici Peter) 16 113
Хеширование равномерное (uniform haghing) 45—46
Хеширование срастающееся (coalesced haghing) 40—45
Хеширование, вторичное скучивание (haghing, secondary clustering) 46—48 85 101—102
Хобби (Hobby John Douglas) 103
Числа Бернулли (Bernoulli's numbers) 65
Числа простые, асимптотика (prime, asymptotics) 66
Числа Стирлинга (Stirling's numbers) 13 82
Числа Фибоначчи (Fibonacci's numbers) 37
Шёнхаге (Schoenhage Arnold) 18 112
Шпигель (Spiegel Murray, R.) 18 20 22 113
Эрдёш (Erdoes Pal) 113
Яо (Yao Andrew Chi-Chin) 7
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте