|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Müller R. — Differential harnack inequalities and the ricci flow |
|
|
 |
| Предметный указатель |
 -exponential map 76 -exponential map 76
 -geodesic 69 74 -geodesic 69 74
Adjoint heat operator 23
Backwards reduced distance 65 75
Backwards reduced volume 65 84
Bianchi identities 13
Christoffel symbols 11
Cigar soliton 5
Connection 11
Convex boundary 31
Cut locus 76
Dirichlet functional 47
Divergence operator 14
Einstein summation 11
Einstein tensor 17
Einstein — Hilbert functional 17
Elliptic operator 28
entropy 65
Entropy for steadies 49
Entropy, gradient 26
Entropy, heat equation 53
Evolution of connection 21
Evolution of curvature 19
Evolution of dV 21
Evolution of Laplacian 21
Evolution of Ricci tensor 19
Evolution of Riemann tensor 19
expanders 24
Exponential map 12
Extended 11
Forward reduced volume 66
Geodesic 68
Hamack inequality for heat kernel 58
Hamack inequality for Ricci flow 43 45
Hamack inequality, Hamilton’s matrix 37
Hamack inequality, Li — Yau 31
Hamack inequality, Perelman’s 64
Hamilton’s matrix Hamack 37
Heat operator 22
Heat operator, adjoint 23
Heat operator, injectivity domain 76
Integrated version 42
Levi — Civita connection 11
Li — Yau Hamack 31
Li — Yau Hamack, integrated version 34
Li — Yau Hamack, quadratic version 32
Lichnerowicz Laplacian 14
Lie-brackets 21
Lie-derivative 24
| Maximum principle 29
Maximum principle for matrices 37
Maximum principle for systems 35
Nash entropy 47
Nash entropy, modified 57
Ni’s entropy 53
Ni’s entropy local version 54
Normal coordinates 12
Parabolic boundary 28
Parabolic cylinder 28
Parabolic interior 28
Parabolic operator 28
Perelman’s 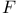 -entropy 49 -entropy 49
Perelman’s 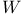 -entropy 62 -entropy 62
Perelman’s 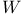 -entropy, local version 62 -entropy, local version 62
Perelman’s Hamack 64
Quadratic version 40
Reduced distance 59
Reduced volume 72
Ricci curvature 12
Ricci flow 17
Ricci flow, backwards 22
Ricci flow, Hamack inequality 43 45
Ricci solitons 24
Riemannian curvature 12
Riemannian metric 11
Scalar curvature 12
Second fundamental form 31
Shrinkers 24
Shrinkers, entropy 62
Shrinkers, gradient 25
Soliton 24
Soliton, cigar 5
Soliton, gradient expander 26
Soliton, gradient shrinker 25
Soliton, gradient steady 24
Space-time, connection 45
Space-time, manifold 45
Space-time, path 46
Stationary metric 17
Steadies 24
Steadies, entropy 49
Steadies, gradient 24
Support function 35
Support function of curvature 15
Support function of dV 16
Support function of Ricci tensor 15
Support function of Riemann tensor 15
Support function, variation 14
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -exponential map
-exponential map 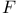 -entropy
-entropy  -entropy
-entropy