|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Routh E.J. — A treatise on dynamics of a particle |
|
|
 |
| Предметный указатель |
Accelerating force 68
Acceleration, Components in three dimensions 490 &c.
Acceleration, Components in three dimensions, Moving axes 498
Acceleration, Components in two dimensions 38
Acceleration, Components in two dimensions, Moving axes 223
Acceleration, Hyper acceleration 233
Adams, J, C, Motion of a heavy projectile 178
Adams, J, C, Proof of Lambert’s theorem 352
Adams, J, C, Resistance to comets 386
Adams, J, C, The true and mean anomalies 347
Algol, Two problems 405
Allegret, Problem on the resistance to a projectile 176 Ex. 4
Ambiguous signs, In Euler’s and Lambert’s theorems in elliptic motion 350 353
Ambiguous signs, In rectilinear motion &c 97 100
Anomaly, Defined 342
Anomaly, Various theorems 346
Apse, Apsidal angle and distances found 367 422
Apse, Apsidal angle and distances found, when independent of the distance 368 370
Apse, Apsidal boundaries 441
Apse, Conditions there are two, one, or no apsidal distances 430-433
Apse, Conical pendulum 564
Apse, Defined, apocentre and pericentre 314
Apse, Equal apsidal distances 434
Apse, Equal apsidal distances, apsidal circle 434 436
Apse, Second approximations 370 426 427
Asymptotic circles, In central orbits 434 446
Atwood, Machine 60
Backlund, Resistance to Encke’s comet 385 note.
Ball, History of mathematics 591 note.
Barrier curves, Boundaries of the field 299
Barrier curves, In brachistochrones and least action 649
Bashforth, Law of resistance 171
Bashforth, Motion of projectiles 169
Bertrand, Brachistochrones 610
Bertrand, Closed orbits 428
Bertrand, General and particular integrals 245
Bertrand, Law of gravitation 393 Ex. 2 3
Bertrand, The apsidal angle 426
Besant, On infinitesimal impulses 148 note.
Bonnet, Superposition of motions 273
Brachistochrones, A conic 605 Ex. 1 606 6
Brachistochrones, A cycloid 601 &c.
Brachistochrones, Case in which the construction fails 649
Brachistochrones, Central force 606
Brachistochrones, In space 591
Brachistochrones, In space, on a cone, cylinder, &c 612
Brachistochrones, In space, on a surface 607
Brachistochrones, Relation to the free path 598 599 606
Brachistochrones, Vertical force 601
Bryant, True and mean anomalies 347 Ex. 5
Burnside and Panton, quoted 489 note.
Callandreau, Encke’s comet 385
Callandreau, On Tisserand’s criterion 415
Callandreau, Spherical swarm 414
Callandreau, The disintegration of comets, page 407
Cardioid, A central orbit 320
Catenary, A brachistochrone 606 Ex. 7
Catenary, A tautochrone 211
Cauchy, Convergency of the series in Kepler’s problem 488
Cayley, Elliptic functions 218 220 364
Cayley, Infinitesimal impulses 150 Ex. 3
Cayley, Lambert’s theorem 352 note.
Cayley, Motion in an ellipse with two centres of force 355 Ex. 4
Central force, Cotes’ spirals 356
Central force, Elementary theorems, &c 306
Central force, Force 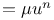 , classification of the orbits 436 , classification of the orbits 436
Central force, Inverse fourth, fifth, &c 364 365
Central force, Locus of centres for a given orbit 421
Central force, Solution by Jacobi’s method in three dimensions 645
Central force, Solution when the velocity is that from infinity 360
Central force, Solution when the velocity is that from infinity, disturbed path 363 Ex. 8
Central force, Solution when the velocity is that from infinity, time 362
Central force, Stability 439
Central force, The inverse cube, rectilinear motion 100
Central force, The inverse cube, rectilinear motion, lemniscate 190 Ex. 11
Centrifugal force, Explained 183
Challis, Infinitesimal impulses quoted 148 note.
Chords of quickest descent, Smooth and rough 143 &c.
Circle, A rough circle 192
Circle, A rough circle, a moving circle 198
Circle, Central force 318 321 190
Circle, coaxial circles 219
Circle, Continuous and oscillatory 216
Circle, Geodesic circles 548 571
Circle, Motion of a heavy particle, time just all round 201 Ex. 1
Circle, Nearly circular orbits 367
Circle, Nearly circular orbits, least action 653
Circle, Nearly circular orbits, second approximation 369 370
Circle, Parallel force 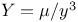 323 452 323 452
Circle, Time in any arc 213
Circle, Two centres of force 194
Circle, When the force is infinite 466
Classification 460
Clerke, History of Astronomy quoted 385 note.
Conic, A brachistochrone 606 Ex. 3 4
Conic, A corresponding curve on an ellipsoid 572
Conic, AS a central orbit with any centre, there are two laws of force 456
Conic, Elements of the conic 457
Conic, Time 454
Conical Pendulum, Apsidal angle 564
Conical Pendulum, Projection a central orbit 560
Conical Pendulum, Radius of curvature 559
Conical Pendulum, Rise and fall 558
Conical Pendulum, Tension 557
Conical Pendulum, The cubic 555
Conical Pendulum, Time of passage 562
Conjugate functions, Relation between the motions 633
Conjugate functions, Relation between the pressures 635
Conservative system, Explained 181
Conservative system, Forces which disappear in the work function 248
Conservative system, Oscillations 294
Constant of gravity 66
Convergency, The series in Kepler’s problem 488 &c.
Coriolis, Theorem on relative vis viva 257
Craig, Particle on an ellipsoid 568
Craig, Treatise on projections referred to 609
Curve, Motion in two dimensions, fixed 181
Curve, Motion in two dimensions, moving 197
Curve, Motion in two dimensions, rough 191
Curve, Three dimensions, changing 533
Curve, Three dimensions, fixed 526
Curve, Three dimensions, moving 528
Cycloid, A brachistochrone 601 602
Cycloid, A brachistochrone, theorems 603 &c.
Cycloid, A tautochrone 204
Cycloid, A tautochrone, rough 212
Cycloid, A tautochrone, theorems 206
Cycloid, Resisting medium 210
Cylinders, Brachistochrones 612 Ex. 3
Cylinders, Motion on 544
Darboux, Elimination of the time in Lagrange’s equations, page 410
Darboux, Force in a conic 450
Darboux, Relation of brachistochrones to geodesics 609
Darboux, The apsidal angle 427
Darwin, Periodic orbits 418 note.
Darwin, Swarm of meteorites, page 407
Degrees of freedom, defined 252
Despeyrons, Problem on time in an arc 203 Ex. 1
Dimensions, General theory 151
Dimensions, In central orbits 316
Direct distance, Central force, &c 325
Direct distance, Time in an arc of lemniscate 201 Ex. 2 3
Direct distance, With this law of force, rectilinear motion with friction 125
Direct distance, With this law of force, rectilinear motion with friction, and resistance 126
Discontinuity, Of a central force 135
Discontinuity, Of brachistochrones 604 649
Discontinuity, Of orbits 467 &c.
Discontinuity, Of resistance 128
Discountinuity, Of friction 125 191
Double answers, In rectilinear motion 98
| Double answers, In two dimensions 266
D’Alembert, The principle 236
Effective force, Defined 68 235
Effective force, Resultant effective force and couple 239
Effective force, Virtual moment 507
Ellipsoid, Cartesian coordinates 568
Ellipsoid, Cartesian coordinates, a case of integration 569 575
Ellipsoid, Central force 570 571 572
Ellipsoid, Elliptic coordinates 576
Ellipsoid, Elliptic coordinates, a case of integration 578 582
Ellipsoid, Motion on a line of curvature 583
Ellipsoid, Spheroidal coordinates 584
Elliptic coordinates, Three dimensions 576
Elliptic coordinates, Translation into Cartesian 576 580
Elliptic coordinates, Two dimensions 585
Elliptic motion, Bessel 480
Elliptic motion, Change of eccentricity and apse, &c. by a resisting medium 383
Elliptic motion, Change of eccentricity and apse, &c. by forces 380
Elliptic motion, Disturbed by continuous forces 376
Elliptic motion, Disturbed by impulses 371 &c.
Elliptic motion, Elliptic velocity 397
Elliptic motion, Kepler’s problem 473
Elliptic motion, Lagrange 479
Elliptic motion, Time found 342 345
Encke, Resistance to a comet 385
Energy, In central forces 313; see also vis viva.
Energy, Principle of 250
Epicycloid, A central orbit 322
Epicycloid, A tautochrone 211
Epicycloid, Force infinite 472 Ex. 2
Equiangular spiral, A central orbit 319
Equiangular spiral, A central orbit, particle at centre of force 470
Equiangular spiral, A tautochrone 211
Equiangular spiral, Moving spiral 198 Ex. 2
Equiangular spiral, Pressure 190 Ex. 8
Euler, Brachistochrones with a central force 591 note.
Euler, Lemniscate 201 Ex. 2
Euler, On motion in a parabola 350
Euler, Problem on a rebounding particle 305 Ex. 4
Euler, With two centres of force 585 note.
Finite diffreences, Problems requiring 305
Foesyth, Differential equations 243
Foesyth, Theory of functions 489
Foucault, Pendulum referred to 57 627
Foucault, Theory 624 626
Friction, Discontinuity 125 191
Friction, Rough chords with gravity 104
Friction, Rough chords with gravity, centre of force 133
Friction, Rough curve 191
Frost, Elliptic velocity 397
Frost, Singular points in a circular orbit 466
Gauss, Coordinates 546 547
Geodesic, Brachistochrones Bertrand 610
Geodesic, Circles on ellipsoid 548
Geodesic, Darboux 609
Geodesic, line 539
Geodesic, Roberts 571
Glaisher, Force in a conic 450 note.
Glaisher, Time in an ellipse 347 Ex. 1 476
Gray and Mathews, Kepler’s problem 481
Gray and Mathews, Treatise on Bessel functions 286 Ex. 9
Greenhill, An integral 116
Greenhill, Conical pendulum 555 note.
Greenhill, Cubic law of resistance 177
Greenhill, Elliptic functions 213 note 364
Greenhill, Motion of projectiles 169
Greenhill, Paths for a central force 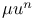 , special values of , special values of  356 note. 356 note.
Greenhill, Stability of orbits and asymptotic circles 429 note
Grouping, Of trajectories of a particle, Theory 636 638
Grouping, Special cases 159 330 339
Guglielmini, Experiments on falling bodies 627
H li li oide, Motion on, another problem 543 Ex. 5 oide, Motion on, another problem 543 Ex. 5
H li li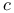 oide, Motion on, Liouville’s solution 583 Ex. 4 oide, Motion on, Liouville’s solution 583 Ex. 4
Haerdtl, Traces path of a planet in a binary system 418 Ex. 2
Hall Maxwell, On Algol 405 Ex. 1
Hall, Asaph, Satellites and mass of Mars 403
Hall, Asaph, Singular points in central orbits 465 note.
Halphan, Force in a conic 450 note.
Halphan, Law of gravitation 393 Ex. 1
Hamilton, Hamiltonian equation 640
Hamilton, Hodograph 394
Hamilton, Law of force in a conic 453
Harmonic oscillation, Definition, frequency, amplitude, &c 119
Helix, Heavy particle on, fixed 527
Helix, Heavy particle on, moving 534
Herschel, Algol 405
Herschel, Disturbed elliptic motion 379
Hill, Stability of the moon’s orbit 417
Hodograph, Central orbits 394
Hodograph, Elementary theorems 29
Hodograph, Itself a central orbit 398
Hopkins, Infinitesimal impulses 148 note.
Horse-power, Defined 72
Huygens, Terminal velocity 111
Impulses, How measured 80
Impulses, Infinitesimal 148
Impulses, Smooth bodies 83 &c.
Inertia, Explained 52 183
Inertia, moment of 241
Infinite, Force 100 466
Infinite, Subject of integration infinite 99 202
Ingall, Motion of projectiles quoted 169
Initial, Initial motion deduce from Lagrange’s equations 517
Initial, Starting from rest 280
Initial, String of particles 279
Initial, Tension and curvature 276 &c.
Initial, Three attracting particles fall from rest 284 Ex. 6
Integrals, A general case in three dimensions 497
Integrals, A general case in three dimensions, in Jacobi’s method 645
Integrals, General and Particular integrals 244 245
Integrals, Integrals of Lagrange’s equations 521 and page 408
Integrals, Liouville’s 522
Integrals, Of the equations of motion, Two elementary 74 75
Integrals, Rectilinear motion 97 101
Integrals, Summary of methods in two dimensions 264
Inverse square, law of, Central force 332 &c; see Time.
Inverse square, law of, Particle falls from a planet 134
Inverse square, law of, Rectilinear motion 130
Inversion, Calculus of variations 650 Ex. 2
Inversion, Of the impressed forces 631 632
Inversion, Of the motion of a particle 628
Inversion, Of the pressure on a curve, &c 631
Jacobi, Case of solution of Lagrange’s equations 523
Jacobi, Criterion of max-min in the calculus of variations 594 648
Jacobi, Integral for a planet in a binary system 255 415 417
Jacobi, Method of solving dynamical problems 640 644
Jacobi, Two centres of force 585 note.
Jellett, On brachistochrones 591 note 650
Kepler, Kepler’s problem 473
Kepler, Law of gravitation in the solar and stellar systems 390
Kepler, The laws 387
Korteweg, Stability, asymptotic circles, &c 429 note.
Lachlan, Treatise on modern geometry referred to 219
Lagrange, Conical pendulum 555 note.
Lagrange, Energy test of stability 296
Lagrange, Two centres of force 585 note.
Lagrange’s equations, Change of the independent variable 524 and page 408
Lagrange’s equations, Elementary resolutions deduced 512 Ex. 1 2
Lagrange’s equations, Elementary resolutions deduced, vis viva deduced, Ex 3
Lagrange’s equations, Elimination of the time, page 409
Lagrange’s equations, Initial motion 517
Lagrange’s equations, Methods of solution 521 and page 408
Lagrange’s equations, Proof 503 &c.
Lagrange’s equations, Small oscillations 513
Lagrange’s equations, Transference of a factor 524
Laisant, On a case of vis viva 258
Lam , On curvilinear coordinates 525 , On curvilinear coordinates 525
Lambert, Time in an elliptic arc 352
Laplace, Convergency 488
Laplace, On three attracting particles 406
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



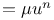 , classification of the orbits
, classification of the orbits 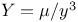
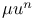 , special values of
, special values of 
 li
li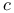 oide, Motion on, another problem
oide, Motion on, another problem