|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Boothby W.M. — An introduction to differentiable manifolds and riemannian geometry |
|
|
 |
| Предметный указатель |
Hopf — Rinow theorem 347
Hyperbolic space 168 404
I(P) 134
Ideal, of an exterior algebra 225
Imbedding, of manifolds 69—74
Imbedding, of manifolds, in  , compact case 196 , compact case 196
Imbedding, of manifolds, in  , general case 197 , general case 197
Immersion of manifolds 69—74
Index of vector field 140
Infinitesimal generator see “One-parameter group action”
Initial conditions for differential equations 131
Inner product 2 184
Int M 253
Integrable functions 231 236
Integrable n-form 236
Integral curve 126
Integral manifold of distribution 159
Integral manifold of distribution, maximal 163
Integral of function on Riemannian manifold 240
Integral of n-form on manifold 239
Integral of n-form on manifold, on  240 240
Integration on manifolds, Lie groups 244—250
Integration on manifolds, manifolds with boundary 251—255
Integration on manifolds, Riemannian manifolds 240
Integration on manifolds, surfaces 241
Invariance of 1-parameter subgroup (under diffeomorphism) 142
Invariance of domain (Brouwer) 10 28
Invariant forms on 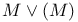 285 285
Invariant forms on Lie groups 246 285
Invariant metric on Lie group 247 353
Invariant vector field 120
Invariant vector field, G-invariant 124
Inverse function theorem 41—46
Irreducible representation 250
Isometric surfaces 377—379
Isometries, group of 353
Isometries, group of, of 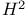 361—362 409—413 361—362 409—413
Isometries, group of, of 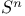 406 406
Isometries, group of, of Euclidean space (rigid motions) 92167 408
Isometry of Euclidean vector spaces 3
Isometry of Riemannian manifolds 191 327
Isometry of Riemannian manifolds, local isometry 402
Isotropic Riemannian manifold 386
Isotropy subgroup 94
Iterated integral theorem 232
Jacobi identity of Lie algebras 152
Jacobian of a mapping 25—26
Jordan content 230
k(s), curvature of plane curve 305
k(s), curvature of space curve 302
K, Gaussian curvature of surface 375
K, quaternions 407
k-frame of  63 63
Klein bottle 13
l, m, n, coefficients of second fundamental form 369
Lattice, integral 85 99
Leibniz rule 33
Length of curve see “Arc length”
Lie algebra 151
Lie algebra, group of automorphisms of 245
Lie algebra, homomorphism of 156
Lie algebra, of Lie group 156
Lie algebra, of subgroup 156
Lie algebra, of vector fields on manifold 151—157
Lie derivative 154 226
Lie group 81—89
Lie group, compact, bi-invariant metric 247
Lie group, compact, bi-invariant volume 247
Lie group, compact, integration on 244—250
Lie group, de Rham groups of 285
Lie group, homomorphism of 85
Lie group, left invariant metric 247
Lie group, representation of 246
Lie group, subgroup of 87—88 142
Lift of mapping 289
Line integral 264
Line integral, independence of path 271
Linear fractional transformations 410
Linear mapping, dual of 177
Linear transformations, field of 206
Local one-parameter group action 127
Loops, product of 268—269
m(A), Lebesgue measure of set 230
Manifold with boundary 11 253
Manifold with boundary, double of 255
Manifolds, abstract 14
Manifolds, differentiable 52—59
Manifolds, imbedding in  196—197 196—197
Manifolds, orientable 13 215—219
Manifolds, topological 6—11
Manifolds, two-dimensional, classification of 14
Mappings, differentiable ( ) on manifolds 65 ) on manifolds 65
Mappings, of Class  26 65 26 65
Mappings, on  25 25
Mappings, smooth 26 67
Mean value theorem 23
Mean value theorem, for mappings 26
Measure zero, set of, in  230 230
Measure zero, set of, in  , on a manifold 235 , on a manifold 235
Metric, Riemannian 186
Minimal surface 376
Mobius band 13
Monkey saddle 376
Motions, rigid, (isometries) on  92 167 408 92 167 408
Motions, rigid, (isometries) on hyperbolic plane 410
N, unit normal to surface 366
Natural basis of  2 30 2 30
Natural isomorphism, tangent spaces to  29 29
Neighborhood see also “Coordinate neighborhoods”
Neighborhood, admissible neighborhood 101
Norm, of vector 3
Normal coordinates 339
Normal section of surface 371
Normal space to submanifold 308
Normal vector to curve 303
Normal vector to surface 366
O(n), orthogonal group 85
One parameter subgroups of Lie groups 147—150 355
One-parameter group action, basic theorem 136
One-parameter group action, examples of 139—146
One-parameter group action, global 123 128
One-parameter group action, infinitesimal generator of 123
One-parameter group action, local 127
Orbit of group action 92
Orbit of group action, of one-parameter group 125 128
Orbit space of group action 93
Order of differentiation, interchange of 24 325
Ordinary differential equations 131—138 172—174
Orientation of manifold 216
Orientation of manifold, of vector space 215
Oriented basis 215
Paracompact space 11 193
Parallel curvature tensor 401
Parallel displacement of vector field 311 323
Parallelizable manifold 119
Parametrization of manifolds 68
Parametrization of submanifold 312
Parametrization of surface 113
Partial derivatives 21
| Partial derivatives, differentiability and 21—22
Partial derivatives, independence of order 24
Partition of unity 193—198
Partition of unity, applications of 195—198
Path 268
Planar point 371
Poincare lemma 278
Positive curvature, spaces of 406
Principal curvatures, of surface 370—373
Principal directions 372
Projective space, real 15 61
Proper function 199
Proper mapping 81
Properly discontinuous action of a group 96 104
Quaternions 407
Quotient space 60
Quotient topology 60
R(X, Y),  , curvature operator 326 , curvature operator 326
R(X, Y, Z, W), curvature tensor 327
Rank of differentiable mapping 47 69 111
Rank of linear transformation 47
Rank of matrix 46
Rank theorem 47—49
Real analytic function 24
Regular covering, by spherical (cubical) neighborhoods 194
Regular domain 254
Representation, of Lie group 249—250
Representation, of Lie group, orthogonal 249
Representation, of Lie group, semisimple 250
Restriction of a differential form 260
Restriction of a differential form, of covector 182
Riemann integral, properties of 231
Riemannian geometry, fundamental theorem of 318
Riemannian manifold 186 192
Riemannian manifold, as metric space 189
Riemannian manifold, differentiation on 317
Riemannian manifold, volume element of 219
Riemannian metric, existence of 195
Rigid motions, group of 89 92
Section of tangent bundle 341
Section on coset space 166
Sectional curvature 385—386
Sectional curvature, geometric interpretation 393
Semisimple Lie group 388
Shape operator 367—368
Simple connectedness 268
Slice of coordinate neighborhood 74 160
Slice of cubical neighborhood 74
Smooth mapping 26
Smooth structure 54
SO(n), special orthogonal group 353
Sphere as manifold 57 80
Starlike set 23
Stokes’s theorem 257
Subgroup of Lie group 87 89
Subgroup of Lie group, closed 88
Subgroup of Lie group, one-parameter 143
Subgroup, discrete 98
Subgroup, isotropy 94 166
Submanifold 73 78
Submanifold property 75
Submanifold, imbedded 73
Submanifold, immersed 70
Submanifold, open 56
Submanifold, regular 77
Submersion 70 74 122
Support of function 194
Surface in Euclidean space 14
Surface in Euclidean space, geometry of 366 374
Symmetric Riemannian manifold 351 357
Symmetric Riemannian manifold, examples of 357—363
Symmetries of curvature tensor 382 384
Symmetrizing mapping 204
System of differential equations 131—139
System of differential equations, autonomous 131
System of differential equations, existence of solutions 131 174
System of differential equations, general case 137
System of differential equations, with parameters 137
T(M),  , , 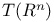 16 116—117 335—336 16 116—117 335—336
T, N, B, tangent, normal, binormal 303
Tangent bundle 16 116—117 335—336
Tangent bundle, sphere bundle 18
Tangent covectors 177—183
Tangent space, as derivations into S 35
Tangent space, at point of  29 32 29 32
Tangent space, at point of M 107—108
Tangent space, to surface 114
Tangent vector to  29—36 29—36
Tangent vector to curve 112
Tangent vector to manifold 107—116
Tensor algebra 208
Tensor field 201—202
Tensor field, covariant derivative of 396—401
Tensor field, invariant 246
Tensor field, parallel 400
Tensors 199—205
Tensors, alternating (skew symmetric) 202
Tensors, alternating mapping 204
Tensors, components of 200
Tensors, exterior product of alternating 209 214
Tensors, linear space of 200
Tensors, multiplication of 208—209
Tensors, symmetric 202
Tensors, symmetrizing mapping 204
Theorema Egregium (Gauss) 18 377
Tietze — Urysohn extension theorem 289
Topological manifold 6—10
Toral group 82
Torsion, of space curve 303
Torus 7 57 80 92
Transitive action of group 92—93 165
Triangulable manifold 243
U,  , coordinate neighborhood 10 52 , coordinate neighborhood 10 52
Umbilical point of surface 371
Universal covering space 296
Vector 1—2
Vector fields 116—122
Vector fields, along submanifold 307
Vector fields, complete 142
Vector fields, constant 311
Vector fields, f-related 120 121
Vector fields, invariant 120
Vector fields, left invariant on Lie group 142 156
Vector fields, Lie algebra of 151
Vector fields, on submanifold 308
Vector fields, on subsets of  37—39 37—39
Vector fields, parallel 311
Vector fields, restriction to submanifold 118
Vector fields, singular points of 140
Vector, norm of 3
Vector, tangent to manifold 107
Velocity vector of moving particle 112 304
Vol D, volume of D, domain of integration 230
Volume element 219
Volume, Riemannian 240
Wedge product 209—214
Weierstrass approximation theorem 197
Whitney imbedding theorem 197
X, Y, Z, vector fields 116—122
[X, Y], (Lie) bracket of vector fields 151
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 , compact case
, compact case 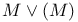
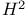
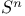
 ) on manifolds
) on manifolds 

 , curvature operator
, curvature operator  ,
, 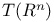
 , coordinate neighborhood
, coordinate neighborhood