|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Okonek C., Schneider M., Spindler H. — Vector Bundles on Complex Projective Spaces |
|
|
 |
| Предметный указатель |
 -invariant pp.114 -invariant pp.114
 -invariant of a holomorpfaic 2-bundle over -invariant of a holomorpfaic 2-bundle over 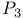 115 115
Atiyah, M.F. 128 129 371
Barth, W. 45 88 228 234 320 367 369 370
Base-change theorem 11
Beilinson, relative version of the theorem of 306
Beilinson, theorem I of 240
Beilinson, theorem II of 245
Birkhoff, G.D. 44
Bogomolov, F.A., unstable in the sense of 190
Bott formula 8
Bundle see vector bundle
Canonical bundle of a projective-algebraic complex manifold 7
Canonical bundle over 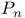 7 7
Cartan formula 14
Cartan — Eilenberg resolution 243
Cartier divisor see divisor
Chern class pp.12
Chern class Chern class of a line bundle 13
Chern class of 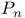 17 17
Chern class of an arbitrary vector bundle 14
Chern class of the hyperplane bundle 14
Chern class, first, of a torsion-free coherent sheaf 160
Chern class, total 14
Chern polynomial of a continous r-bundle over 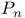 112 112
Coherence theorem 10
Cohomology ring, singular, of 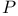 12 12
Conormal bundle of a Cartier divisor on a complex manifold 4
Conormal bundle of a locally complete intersection in 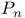 91 91
Conormal bundle of the zero locus of a section 91
Dedekind, R. 44
Degree of a divisor 5
Degree of homogeneity of a vector bundle 63
Descente lemma 195
Determinant bundle of a torsion-free coherent sheaf 154
Discriminant of a 2-bundle over I» 168
Divisor, Cartier 3
Divisor, effective 3
Dual class of a r-codimensional submanifold in. a complex manifold 20
Elencwajg, G. 46 70 71 74 235 237 370
Ellingsrud, G. 368
Endomorphism, regular 332
Euler characteristic 359
Euler sequence 6
Euler sequence, relative 305
Exponential sequence 18
Extension of line bundles 29
Extension, maximal normal, of a subsheaf in a reflexive sheaf 159
Extension, normal, of a subsheaf in a reflexive sheaf 157
Family of stable r-bundles 272
Ferrand, D. 269 .
Forster, O. 46 237
Fundamental class of 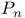 12 12
Geyer, W.D. 44
Gieseker semi-stable 173 see
Gieseker stable torsion-free coherent sheaf 173 see
Gieseker, D. 139 173 191 366 368
Grauert — Muelich theorem 206
Grauert, H. 44
Grothendieck, A., theorem of 22
Harder — Narasimhan-filtration pp.60
Hartshorne, R. 89 110 370
Hartshorne, R., theorem of 343
Hilbert polynomial 272
Hilbert, D. 44
Hirschowitz, A. 70 71
Holomorphic structures on topological bundles pp.111 117 122 128 130
Homogeneous holomorphic r-bundle see vector bundle
Homological codimension 140
Homological dimension 139
Horrocks, G. 39 45 109 128 240 270
Horrocks, G., splitting criterion of 39
Horrocks, G., theorem of 39
Hulek, K. 45 236 332 367 369
Hulek, K., theorem of 332
Hulsbergen, W. 369
Hyperdirect image of a complex 243
Hyperplane bundle over 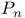 4 4
Indecomposable r-bundle see vector bundle
Instanton bundle, complex, of rank 2 370
Instanton bundle, real, of rank 2 37
Jump line pp.26
Jump line of second kind 236
Jump line, set of 29
k-homogeneous bundle see vector bundle
Koszul complex of a section in a 2-bundle 92
Kronecker module, stable, of rank 2 321
Kronecker module, symmetric stable 350
le Potier 273 367 368
Line bundle is simple 75
Line bundle is stable 164
Line bundle, tautological, over 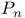 4 4
Local fundamental isomorphism 96
Locally complete intersection pp.90
Lower term sequence 95
Maruyama, M. 139 177 228 272 320 366 367
Moduli of stable 2-bundles pp.271
Moduli space pp.271
Moduli space, 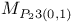 364 364
Moduli space, 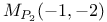 344 344
Moduli space,  is a fine moduli space 319 is a fine moduli space 319
Moduli space,  350 350
Moduli space, 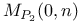 is a coarse moduli space 306 is a coarse moduli space 306
Moduli space, 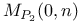 is a fine moduli space for n odd 311 is a fine moduli space for n odd 311
Moduli space, 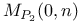 is irreducible 320 is irreducible 320
Moduli space, coarse 274
Moduli space, construction of  pp.313 pp.313
Moduli space, construction of  pp.275 pp.275
| Moduli space, construction of the, for stable 2-bundles on 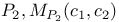 pp.271 pp.271
Moduli space, fine 273
Monad pp.238
Monad over a compact complex manifold 239
Monad, canonically associated to a stable bundle 307
Monad, cohomology bundle of a self dual 282
Monad, cohomology of 239
Monad, display of 239
Mumford, D. 109 160 189 270
Nakayama-Lemma 3
Normal sheaf see sheaf
Null correlation bundle is simple pp.77
Null correlation bundle, Chern classes of the 80
Null correlation bundle, is stable 180
Null correlation bundle, Moduli space of the, over JP- 364
Null correlation bundle, over 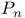 , n odd pp.76 , n odd pp.76
Plemelj, J. 44
Postnikov tower 115
Projection formula 12
Projective bundle, associated to a vector bundle 13
r-bundle see vector bundle :
Rank of a coherent analytic sheaf 145
Rees, E. 128 129 137
Reflexive sheaf 149 see
Remmert, R. 44
Sato, E. 70 71 89
Schwarzenberger, R.L.E. 44 71 112 117 168 191 357
Schwarzenberger, R.L.E., condition of 113
Semicontinuity theorem 10
Semistability see semi-stable sheaf and semi-stable vector bundle
Serre duality 7
Serre duality, Theorem A of 9
Serre duality, Theorem B of 10
Serre, J.P. 81 98 110
Seshadri, C.S. 44
Sheaf of ideals of a Cartier divisor 4
Sheaf, determinant bundle of a torsion-free coherent 154
Sheaf, first Chern class of a torsion-free coherent 160
Sheaf, generated by global sections 9
Sheaf, Gieseker semi-stable 173
Sheaf, Gieseker stable 173
Sheaf, k-th syzygy 145
Sheaf, normal coherent 150
Sheaf, normalized torsion-free 165
Sheaf, reflexive 149
Sheaf, semi-stable, over 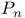 160 160
Sheaf, stable, over 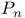 161 161
Sheaf, torsion-free coherent 147
Simple bundle 74 see
Singularity set of a coherent analytic sheaf 144
Singularity set of the homological codimension of a coherent analytic sheaf 144
Smith, L. 137
Spindler, H. 235
Splitting criterion of Horrocks 39
Splitting of vector bundles pp.21
Splitting principle 15
Splitting type of a bundle on a line in 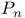 27 27
Splitting type of the tangent bundle over 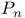 27 27
Splitting type, generic 29
Stability see stable sheaf and stable vector bundle
Stable vector bundle 161 see
Standard construction pp.46
Standard diagramm 48
Strjzfrnme, S.A. 368
Syzygy sheaf 145 see
Syzygy theorem 140
Takemoto, F. 160 189
Tangent bundle is homogeneous 28
Tangent bundle is indecomposable 74
Tangent bundle is simple 74
Tangent bundle is stable 181
Tangent bundle is uniform 27
Tangent bundle, Chern classes of 17
Tangent bundle, holomorphic, of 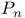 6 6
Tango, H. 81 88
Tautological 2-bundle over G 47
Tautological line bundle over the associated projective bundle 4
Theorem A 9
Theorem B 10
Tjurin, A.N. 89
Torsion-free sheaf 147 see
Uniform bundle 27 see
Universal local deformation of a bundle 311
Van de Ven,A. 70 88 211 234
Vector bundle, associated to a locally complete intersection pp.90
Vector bundle, canonical, over IP 7
Vector bundle, Gieseker semi-stable 173
Vector bundle, Gieseker semi-stable is semistable 174
Vector bundle, Gieseker stable 173
Vector bundle, Gieseker stable is simple 174
Vector bundle, homogeneous 28
Vector bundle, indecomposable 74
Vector bundle, indecomposable of rank (n-1) over 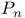 73 73
Vector bundle, k-homogeneous 62
Vector bundle, non homogeneous uniform of rank 3n-1 pp.62
Vector bundle, semi-stable 161
Vector bundle, simple 74
Vector bundle, simple of rank n-1 over 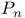 81 81
Vector bundle, stable 161
Vector bundle, stable is Gieseker stable 174
Vector bundle, stable is simple 172
Vector bundle, uniform 27
Vector bundle, uniform of rank r over 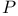 , r<n pp.51 , r<n pp.51
Vector bundle, unstable in the sense of Bogomolov 190
Vogelaar, J-.A. 130 131 135
Ward, R.S. 371
Weber, H. 44
Yang — Mills fields 371 .
Zero locus of a section in a bundle 91
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -invariant
-invariant 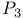
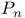
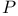
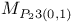
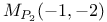
 is a fine moduli space
is a fine moduli space 
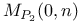 is a coarse moduli space
is a coarse moduli space