|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Köthe G. — Topological vector spaces II |
|
|
 |
| Предметный указатель |
 -space 110 -space 110
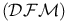 304 304
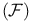 , , 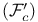 , , 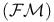 303 303
 211 211
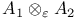 277 277
 187 187
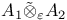 275 275
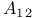 277 277
 , ,  153 153
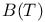 -space 27 -space 27
 -complete 26 -complete 26
 266 266
 111 111
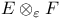 , , 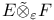 243 243
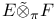 179 179
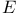 , , 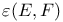 242 242
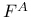 134 134
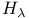 -space 119 -space 119
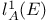 290 290
![$l^1_A[E]$](/math_tex/ac9bbbe074e1d7fcf6462335b0f9e17f82.gif) 292 292
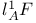 198 198
 258 258
 , ,  199 199
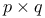 176 176
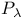 -space 117 -space 117
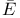 44 44
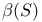 258 258
 -metric approximation property 260 -metric approximation property 260
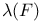 291 291
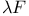 196 196
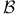 , , 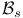 50 50
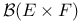 , , 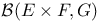 154 154
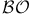 78 78
 168 168
 \mathcal{C}^l(c)$ 51 \mathcal{C}^l(c)$ 51
 , , 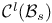 50 50
 , , 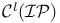 , ,  50 50
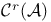 , ,  , , 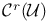 76 76
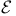 167 242 167 242
 50 50
 257 257
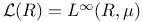 259 308 259 308
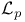 -space, -space, 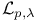 -space 228 -space 228
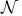 78 78
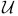 76 76
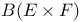 , ,  154 154
 166 166
 200 200
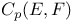 200 200
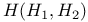 212 212
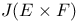 294 294
 1 1
 304 304
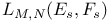 134 134
 131 131
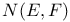 214 214
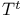 44 44
 73 73
 95 95
 166 166
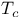 201 201
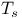 166 166
 73 73
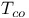 232 232
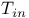 266 266
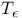 268 268
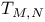 166 166
 131 131
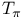 177 177
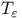 167 167
 205 205
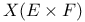 156 156
 156 156
 156 156
 156 156
 168 168
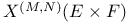 156 156
 156 156
 -norm 178 -norm 178
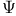 181 181
 -locally topological 301 -locally topological 301
 -hypocontinuous bilinear form 244 -hypocontinuous bilinear form 244
 -hypocontinuous trilinear form 272 -hypocontinuous trilinear form 272
 -product 242 -product 242
 -tensor product 243 -tensor product 243
 -topology 266 -topology 266
 90 90
 160 160
(DFM)-space 303
(S)-space 45
(u)-space 77
Adasch, N. 1 44 46 47 48 49 80 93 97 144 301
Adasch’s open mapping theorem 48
Approximation property 222 232
Aronszajn, N. 230
Associated barrelled space 44
Associated ultrabornological space 73
B-complete 26
Baire space 25 43
Baker, J.W. 100 105 118
Banach disk 70
Banach — Mackey theorem 135 168
Banach, S. 235 249 253
Banach-Steinhaus theorem 141 142
Basis 248
Basis, problem 253
Batt, J. 210
Bessaga, C. 249
Bi-equicontinuous topology 167
Bibounded topology 166
Bierstedt, K.D. 244 246 257 289 300
Bounded approximation property 26
Bounded mapping 160
Bourbaki, N. 9 43 153 155 163 200 258
Browder, F. 80 105 124
Buchwalter, H. 300 301 302 303
C(X, E) 286
Canonical bilinear mapping x 173
CB(S) 257
Closable 81
Closed for the Mackey convergence 15
Closed mapping 34
Co-extension property 228
Compact extension property 227
Compact lifting property 229
Compact mapping 200
Compatible topology 264
completely continuous 207
Conjugate element 211
Continuity theorems 158 159 160 161
Continuous contraction 87
Continuous left inverse 115
Continuous refinement 96
Continuous right inverse 115
Countably barrelled 142
Cross, R.W. 112
d(E, F) 228
Davie, A.M. 235 244
De Wilde, M. 1 53 54 56 65 66 67 69 70 73 75 78 79 203 249 250 253 284
De Wilde’s closed-graph theorem 57
Dense mapping 80
Densely defined mapping 80
Detachable 118
Diestel, J. 317 319
Dieudonne, J. 22 43 255
Distance coefficient 228
Domain of definition 34
Duality theorems of Buchwalter 301 302
Dugundji, J. 231
Dunford — Pettis property 210
| D[M, N] 174
e 74
Eberhardt, V. 46 49 76 78 116
Edwards, R.E. 210 249
Eidelheit, M. 125 126
Enflo, P. 130 235 244 247 248 253 260 262 264
Equibounded 160
Equicontinuous basis 248
Equicontinuous topology 167
Equihypocontinuous 158
Ernst, B. 301
Extended kernel 81
Fast convergent 70
Fast convergent, null sequence 71
Figiel, T. 260
Fillmore, P.A. 111
Finite section 292
Fully solvable 126
Gantmacher, V. 205
Garnir, H.G. 203
Goldberg, S. 65 106 124 210
Goodner, P. 118
Graph topology 95
Grathwohl, M. 76
Grothendieck, A. 8 19 21 22 44 53 54 61 63 68 120 130 131 140 143 152 153 160 164 165 169 171 176 183 193 202 204 210 214 224 232 234 235 243 260 264 305 315 317 318 319
Hagemann, E. 31
Hahn, H. 113
Hasumi, M. 118
Hellinger — Toeplitz theorem 40 41
Hellinger, E. 40
Helly, E. 113
Henriques, G. 255
Hilbert — Schmidt mapping 212
Hilbert — Schmidt norm 212
Hogbe — NIend, H. 232 246 248
Hollstein, R. 274 302 304
Holub, J.R. 285 286
Homomorphism theorem 8
Homomorphism theorem for (B)-spaces 17
Homomorphism theorem for (F)-spaces 18
Husain, T. 27 28 49 142
Hypercomplete 31
Hypocontinuous 155 166
Ichinose, T. 286
Inductive tensor product 266
Inductive tensor product, topology 266
Infinite-nuclear 226
Infinite-nuclear norm 227
Infra-(s)-space 44
Infra-(u)-space 77
Infra-Ptak space 26
Injective tensor product 266
Injective topology 266
Integral bilinear form 294
Integral mapping 304
Integral norm 294
Invariant subspace 230
Johnson, W.B. 131 260 261 262
Kaballo, W. 280
Kalton, N.J. 1 50 51 52 53 255
Kalton’s closed-graph theorems 50 51 53
Kato, K. 65 66 210
Kaufmann, R. 118
Kelley, J.L. 1 31 32 49 79 118
Komura, Y. 1 44 45 76 78
Komura’s closed graph theorem 45
Kothe, G. 17 21 31 40 43 47 67 118 119 120 203 297
Krein — Smulian property 31
Krishnamurthy, V. 123 124
L(E, F) 133
Lacey, E. 210
Landsberg, M. 230
Liftable 118
Lifting property 19
Lindenstrauss, J. 118 120 130 228 231 254 263
Lindenstrauss’ theorem 228
Linear equation 111
Localization theorem 67
Locally closed 15
Locally complete 135
Locally convex algebra 170
Locally sequentially invertible 15
Locally topological 301
Lomonosov, V.I. 130 231
Lotz, H.T. 296
Loustaunau, J.O. 123 124
Macintosh, A. 79
Mackey — Ulam theorem 72
Mahowald, M. 38 50 52 53 75
Marti, J.T. 254
Martineau, A. 54 79
Maximal slight extension 91
McArthur, C.W. 254
Meise, R. 244 246 289 300
Metric approximation property 260
Mitiagin, B.S. 319
Mochizuki, N. 122
Nachbin, L. 118
Nakamura, M. 205
Nearly continuous 36
Nearly open 24
Neubauer, G. 170
Neumann, J.von 176
Newns, H.F. 249
Niethammer, W. 127
Nuclear mapping 214
Nuclear norm 215
Open mapping theorem of Adasch 47 48
Partition of unity 255
Pelczynski, A. 120 130 210 228 247 249 260
Persson, A. 49
Pettis-integral 318
Phillips, R.S. 117 258 260
Pietsch, A. 183 196 216 289 292 314 319
Pitt, H.R. 208
Powell, M. 74 76
Precompact mapping 200
Prenuclear 314
Principle of uniformed boundedness 135
Projective norm 178
Projective tensor product 177
Projective topology 177
Ptak space 26
Ptak, V. 1 23 24 27 30 37 41 49 67
Q[A] 81
Radon — Nikodym property 319
Raikow, D.A. 54 78
Randtke, P.J. 226 228
Reduced locally convex kernel 192
Regular contraction 86
Regular mapping 80
Riemann, B. 289
Robertson, A.and W. 1 14 48 49 67 79 144 145 183 184
Rosenthal, H.P. 210 228
Saturated, saturated cover 131
Scalar net 31
Scalarly complete 31
Schaefer, H. 176 200
Schatten, R. 131 176 297 317
Schauder basis 248
Schauder, L. 130 202 254 269
Schmets, J. 203
Schwartz, L. 43 54 79 131 176 193 232 243 260 271 284 289
Separately continuous 158
Sequentially closed mapping 56
Sequentially continuous 157
Sequentially invertible 13
Sequentially separable 254
Simons, S. 218
Simple topology 133 166
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -space
-space 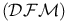
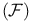 ,
, 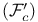 ,
, 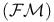

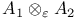

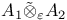
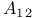
 ,
, 
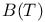 -space
-space  -complete
-complete 

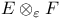 ,
, 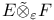
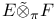
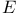 ,
, 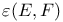
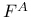
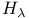 -space
-space 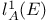
![$l^1_A[E]$](/math_tex/ac9bbbe074e1d7fcf6462335b0f9e17f82.gif)
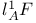

 ,
, 
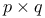
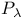 -space
-space 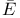
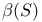
 -metric approximation property
-metric approximation property 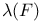
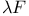
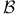 ,
, 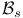
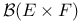 ,
, 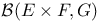
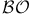

 \mathcal{C}^l(c)$
\mathcal{C}^l(c)$  ,
, 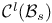
 ,
, 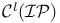 ,
, 
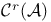 ,
,  ,
, 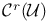
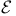


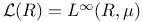
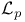 -space,
-space, 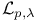 -space
-space 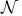
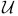
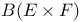 ,
, 


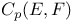
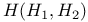
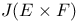


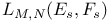

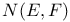
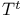



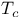
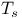

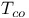
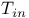
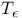
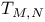

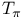
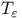

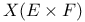




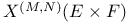

 -norm
-norm 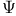
 -locally topological
-locally topological  -hypocontinuous bilinear form
-hypocontinuous bilinear form 
