јвторизаци€
ѕоиск по указател€м
Neeman A. Ч Triangulated categories
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Triangulated categoriesјвтор: Neeman A. јннотаци€: The first two chapters of this book offer a modern, self-contained exposition of the elementary theory of triangulated categories and their quotients. The simple, elegant presentation of these known results makes these chapters eminently suitable as a text for graduate students. The remainder of the book is devoted to new research, providing, among other material, some remarkable improvements on Brown's classical representability theorem. In addition, the author introduces a class of triangulated categories" Ч the "well generated triangulated categories" Ч and studies their properties. This exercise is particularly worthwhile in that many examples of triangulated categories are well generated, and the book proves several powerful theorems for this broad class. These chapters will interest researchers in the fields of algebra, algebraic geometry, homotopy theory, and mathematical physics.
язык: –убрика: ћатематика /јлгебра /“еори€ категорий /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 2001 оличество страниц: 449ƒобавлена в каталог: 12.03.2005ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
Abelian categories of product-preserving functors 183Ч214 Abelian categories of product-preserving functors are locally presentable 221Ч224 326 Abelian categories of product-preserving functors do not satisfy [AB5], [AB5*] 209Ч210 Abelian categories of product-preserving functors have enough projectives 212 Abelian categories of product-preserving functors may not have cogenerators 403Ч405 Abelian categories of product-preserving functors satisfy [AB3*] 186Ч187 200 Abelian categories of product-preserving functors satisfy [AB3] 196Ч200 Abelian categories of product-preserving functors satisfy [AB4*] 206 Abelian categories of product-preserving functors satisfy [AB4] 207Ч209 Abelian categories of product-preserving functors via universal homological functor 384Ч385 Abelian categories of product-preserving functors, coproducts 191 Abelian categories of product-preserving functors, definitions 185 Abelian categories of product-preserving functors, homological functors 204Ч205 Abelian categories of product-preserving functors, homological objects 224Ч229 258Ч262 Abelian categories of product-preserving functors, homological objects, as filtered colimits of representables 226Ч229 Abelian categories of product-preserving functors, homological objects, characterisation in terms of vanishing Ext 258Ч259 Abelian categories of product-preserving functors, homological objects, Embedding arbitrary objects in homological ones 259Ч262 Abelian categories of product-preserving functors, homological objects, stable under filtered colimits 225 Abelian categories-review of formalism 321 Abelian categories-review of formalism 354 Abelian categories-review of formalism 378 Abelian categories-review of formalism 345Ч361 Abelian categories-review of formalism 349Ч351 Abelian categories-review of formalism 358 Abelian categories-review of formalism 350 Abelian categories-review of formalism 350Ч354 359Ч361 Abelian categories-review of formalism 348 Abelian categories-review of formalism 346Ч348 370Ч371 Abelian categories-review of formalism 356 Abelian categories-review of formalism 355Ч356 Abelian categories-review of formalism 329 Abelian categories-review of formalism 328 Abelian categories-review of formalism 332Ч334 Abelian categories-review of formalism 334Ч335 338Ч339 Abelian categories-review of formalism 321 324Ч327 Abelian categories-review of formalism 327Ч328 Abelian categories-review of formalism 343Ч345 Abelian categories-review of formalism 327Ч345 Abelian categories-review of formalism 327 Abelian categories-review of formalism 346 Abelian categories-review of formalism 355 Abelian categories-review of formalism 361Ч366 Adjoints of a triangulated functor is triangulated 179 Adjoints, A(-) preserves and reflects adjoints 181Ч182 Adjoints, Bousfield localisation 288 309Ч318 Adjoints, Brown representability 286Ч287 Bousfield localisation 288 309Ч318 Bousfield localisation for homology theory E 417Ч418 Bousfield localisation is selfdual 315Ч316 Bousfield localisation, embedding the quotient 316Ч317 Bousfield localisation, existence 288 318 Bousfield localisation, local object 310 Bousfield localisation, perpendicular subcategories 313 Brown representability 275 Brown representability for 282Ч284 Brown representability for dual of E-acyclic spectra 419Ч420 Brown representability for duals of well-generated categories 303Ч306 Brown representability for E-acyclic spectra 417Ч418 Brown representability for E-local spectra 417Ч418 Brown representability for spectra 408 Brown representability for well-generated categories 285Ч286 Brown representability, adjoints 286 Brown Ч Comenetz objects 302Ч303 307 Cardinal of 410Ч411 Cardinal, regular 103 Cardinal, singular 103 Cofinal sequences 358 Compact generating set 274 Compact objects 130 Compact objects in quotient 138 143Ч144 Compact objects, filtrations by coproducts 371Ч378 Compact objects, generators for 140 Compact objects, subcategory of 129 Compact objects, subcategory of, inclusion relations 129 Compact objects, subcategory of, is localising 130 Compactly generated categories 274 Existence of products 288 Filtrations by coproducts of compact objects 371Ч378 Freyd's universal abelian category 153Ч182 Freyd's universal abelian category, 169 Freyd's universal abelian category, 161 Freyd's universal abelian category, A(-) is a functor, and preserves products 177Ч179 Freyd's universal abelian category, A(-) is a functor, and preserves products, 169 Freyd's universal abelian category, A(-) is a functor, and preserves products, 161 Freyd's universal abelian category, A(-) is a functor, and preserves products, A(-) preserves and reflects adjoints 181Ч182 Freyd's universal abelian category, A(-) is a functor, and preserves products, category 162Ч163 Freyd's universal abelian category, A(-) is a functor, and preserves products, category 167Ч169 Freyd's universal abelian category, A(-) is a functor, and preserves products, category 172Ч173 Freyd's universal abelian category, A(-) is a functor, and preserves products, coproducts in 169Ч171 Freyd's universal abelian category, A(-) is a functor, and preserves products, definition of 154 Freyd's universal abelian category, A(-) is a functor, and preserves products, example of non-well-powered 394 Freyd's universal abelian category, A(-) is a functor, and preserves products, functors in 154 Freyd's universal abelian category, A(-) is a functor, and preserves products, relation with 214Ч220 Freyd's universal abelian category, A(-) is a functor, and preserves products, subobjects and quotient objects 172Ч177 Freyd's universal abelian category, A(-) is a functor, and preserves products, universal homological functor 163Ч164 Freyd's universal abelian category, A(-) preserves and reflects adjoints 181Ч182 Freyd's universal abelian category, category 162Ч163 Freyd's universal abelian category, category 167Ч169 Freyd's universal abelian category, category 172Ч173 Freyd's universal abelian category, coproducts in 169Ч171 Freyd's universal abelian category, definition of 154 Freyd's universal abelian category, example of non-well-powered 394 Freyd's universal abelian category, functors in 154 Freyd's universal abelian category, have enough projectives 153Ч154 Freyd's universal abelian category, relation with 214Ч220 Freyd's universal abelian category, subobjects and quotient objects 172Ч177 Freyd's universal abelian category, universal homological functor 163Ч164 Functor 215 Functor 215Ч216 Functor 216Ч218 290 Functor 289Ч290 Functor 214Ч215 Functor 218 Functor categories, abelian categories of product-preserving functors 183Ч214 Functor categories, abelian categories of product-preserving functors, are locally presentable 221Ч224 326 Functor categories, abelian categories of product-preserving functors, coproducts 191 Functor categories, abelian categories of product-preserving functors, definitions 185 Functor categories, abelian categories of product-preserving functors, do not satisfy [AB5], [AB5*] 209Ч210 Functor categories, abelian categories of product-preserving functors, Embedding arbitrary objects in homological ones 259Ч262 Functor categories, abelian categories of product-preserving functors, have enough projectives 212 Functor categories, abelian categories of product-preserving functors, homological functors 204Ч205 Functor categories, abelian categories of product-preserving functors, homological objects 224Ч229 258Ч262 Functor categories, abelian categories of product-preserving functors, homological objects characterised in terms of vanishing Ext 258Ч259 Functor categories, abelian categories of product-preserving functors, may not have cogenerators 403Ч405 Functor categories, abelian categories of product-preserving functors, relation with Freyd's universal abelian category 214Ч220 Functor categories, abelian categories of product-preserving functors, satisfy [AB3*] 186Ч187 200 Functor categories, abelian categories of product-preserving functors, satisfy [AB3] 196Ч200 Functor categories, abelian categories of product-preserving functors, satisfy [AB4*] 206 Functor categories, abelian categories of product-preserving functors, satisfy [AB4] 207Ч209 Functor categories, abelian categories of product-preserving functors, via universal homological functor 384Ч385 Functor, kernel of 74 99 Functor, representability 275 Functor, representability, for 282Ч284 Functor, representability, for duals of well-generated categories 303Ч306 Functor, representability, for well-generated categories 285Ч286 Functor, triangulated 73 Generating set 205 273Ч274 Generating set a category without 438Ч441 Generating set in the dual of well-generated categories 302Ч303 Generating set, compact 274 Generating set, compactly generated categories 274 Generating set, generate category 285 Generating set, perfect 273Ч274 Generating set, well generated categories 274 Gluing data 318Ч319 Good morhism of triangles 52 Good object in a subcategory 113 Grothendieck's duality theorem 306 Homological functor as object in 224Ч229 258Ч262 Homological functor as object in 226Ч229 Homological functor as object in 258Ч259 Homological functor as object in 259Ч262 Homological functor as object in 225 Homological functor into abelian functor categories 204Ч205 Homological functor, definition 32 Homological functor, examples 32 Homological functor, universal 163Ч166 Homological functor, universal into [AB5*] 384Ч385 Homotopy cartesian square 52 Homotopy colimits of subsequences 68Ч70 Homotopy colimits, definition 63 Homotopy colimits, elementary properties 64Ч65 Homotopy pullback 54Ч55 183Ч184 Homotopy pushout 53Ч54 Idempotent splitting 65 Kernel of functor 74 99 Large categories 99Ч100 Limits 321 Local object in abelian category 329 Local object in triangulated category 310 Localisation, Bousfield 288 309Ч318 Localisation, Bousfield, embedding the quotient 316Ч317 Localisation, Bousfield, existence 288 318 Localisation, Bousfield, is selfdual 315Ч316 Localisation, Bousfield, local object 310 Localisation, Bousfield, perpendicular subcategories 313 Localisation, Thomason 143Ч144 Localisation, Verdier 74Ч99 309 Localisation, Verdier, existence theorem 74Ч75 Localisation, Verdier, size of Hom-sets 99Ч100 137 318 Localising subcategory 106Ч107 Localising subcategory of small objects 126 Locally presentable categories 221Ч224 321 324Ч327 Mapping cone, definition 45 Mapping cone, [TR4] 51 Modules 387Ч388 Modules 391 Modules 390Ч391 Modules 390 Octahedral axiom 58 60 Perfect classes, definition 110Ч111 Perfect classes, maximal 120Ч121 Perfect classes, new out of old 111 116 119 Perfect classes, which are triangulated subcategories 115 Perfect generating set 273Ч274 Perfectly generated category 274 Perfectly generated category, 432Ч437 Phantom maps 219Ч220 Phantom maps and injectives in 299Ч300 Phantom maps and right adjoint to 301 Phantom maps annihilated by homological functors into [AB5*] categories 383Ч384 Phantom maps as the kernel of 218Ч219 Phantom maps from coproducts of compacts vanish 369Ч370 Phantom maps in 438Ч440 Phantom maps, definition 219 Phantom maps, existence for every 219Ч220 Pretriangle, definition 33 Pretriangle, examples 34 Pretriangle, new out of old 34 49 Pretriangulated category 29 70 Pretriangulated category, definition 29 Products of triangles are triangles 37 Products, existence of 288 Quotient categories 74Ч99 309 Quotient categories, commutative squares 85Ч86 Quotient categories, compact objects 143Ч144 Quotient categories, embedding via Bousfield localisation 316Ч317 Quotient categories, equality of morphisms 84Ч85 Quotient categories, existence 74Ч75 84 Quotient categories, isomorphisms 90 92 Quotient categories, preservation of products 107 110 Quotient categories, size of Hom-sets 99Ч100 137 318 Quotient categories, zero objects 91 Regular cardinal 103 Representability of functors 275 Representability of functors for 282Ч284 Representability of functors for duals of well-generated categories 303Ч306 Representability of functors for well-generated categories 285Ч286 Serre subcategories 327 Singular cardinal 103 Six functors 318Ч319 Small categories 99Ч100 137 Small hom-sets 99Ч100 137 318 Small object, definition 123 Small object, subcategory of 124 Small object, subcategory of, is localising 126 Small object, subcategory of, is triangulated 124 Spectra, 425 Spectra, Bousfield localisation for homology 417Ч418 Spectra, Brown representability 408 Spectra, cardinal of 410Ч411 Spectra, E-acyclics 411Ч412 Spectra, E-acyclics, are well-generated 417Ч418 Spectra, E-acyclics, Brown representability 417Ч418 Spectra, E-acyclics, Brown representability for dual 419Ч420 Spectra, E-local 419 Spectra, E-local, are well-generated 417Ч418 Spectra, E-local, Brown representability 417Ч418 Spectra, elementary properties 407Ч408 Spectra, functor to D(R) 420 Spectra, functor to D(R), descends to 422Ч425 Spectra, functor to D(R), respects 420Ч421 Splitting, idempotent 65 Splitting, triangle with 0 42Ч45 Subcategory of compact objects 129 130 Subcategory of compact objects, inclusion relations 129 Subcategory of compact objects, is localising 130 Subcategory of small objects 124 Subcategory of small objects is localising 126 Subcategory of small objects is triangulated 124 Subcategory, generated by a set 103Ч104 106Ч107 Subcategory, localising 106Ч107 Subcategory, thick 74 99 Subcategory, thick closure 75 99 147Ч149 Subcategory, triangulated 60 Thomason localisation 143Ч144 Thomason localisation, applied to finding 409 TR0 29 TR1 29 TR2 29 TR3 30 TR4, equivalent formulations 51 60 TR5, dual 63 TR5, statement 63 Triangles, contractible 47 48 Triangles, distinguished 29 Triangles, products of 37 Triangles, summands of 38 Triangulated subcategories, which are perfect classes 115 Universal homological functors 163Ч166 384Ч385 Verdier localisation 74Ч99 309 Verdier localisation, existence theorem 74Ч75 Verdier localisation, size of Hom-sets 99Ч100 137 318 Well generated categories 274 Well generated categories are unions of 285Ч286 Well generated categories, duals satisfy Brown representability 303Ч306 Well generated categories, neither 437Ч441 Well generated categories, not both T and T op 427Ч431 Well generated categories, satisfy Brown representability 285Ч286
–еклама
 |
|
ќ проекте
|
|
ќ проекте



 -filtered limits
-filtered limits  )]
)] 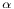 ]
] 
 -perfectly generated categories
-perfectly generated categories 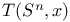
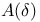 is a Frobenius category
is a Frobenius category 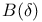 and its equivalence with
and its equivalence with 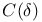 and its equivalence with
and its equivalence with  and its equivalence with
and its equivalence with  satisfies [TR5]
satisfies [TR5]  , Ab
, Ab 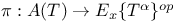 , Ab is exact and respects coproducts
, Ab is exact and respects coproducts 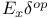 , Ab
, Ab 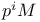 , definition
, definition 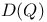 is not
is not 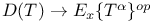 , Ab
, Ab 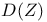
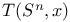
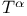
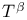
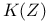 nor
nor