Авторизация
Поиск по указателям
Bergeron F., Labelle G., Leroux P. — Combinatorial Species and Tree-like Structures
Обсудите книгу на научном форуме Нашли опечатку?
Название: Combinatorial Species and Tree-like StructuresАвторы: Bergeron F., Labelle G., Leroux P.Аннотация: The combinatorial theory of species, introduced by Joyal in 1980, provides a unified understanding of the use of generating functions for both labelled and unlabelled structures and as a tool for the specification and analysis of these structures. Of particular importance is their capacity to transform recursive definitions of tree-like structures into functional or differential equations, and vice versa. The goal of this book is to present the basic elements of the theory and to give a unified account of its developments and applications. It offers a modern introduction to the use of various generating functions, with applications to graphical enumeration, Polya theory and analysis of data structures in computer science, and to other areas such as special functions, functional equations, asymptotic analysis and differential equations. This book will be a valuable reference to graduate students and researchers in combinatorics, analysis, and theoretical computer science.
Язык: Рубрика: Математика /Алгебра /Комбинаторика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1998Количество страниц: 457Добавлена в каталог: 10.03.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Generating series, type 15 84 106 122 Good — Lagrange inversion formula 200 203 220 Good's formula (one dimensional) 183 Graphs, 2-connected 299 Graphs, 2-edge-connected 300 307 Graphs, complete 297 Graphs, constructed on vertices and edges 111 114 Graphs, directed 7 74 76 77 409 411 415 Graphs, discrete 297 Graphs, even 351 Graphs, Husimi 300 Graphs, multigraphs 114 308 Graphs, non-separable (or 2connected) 299—304 Graphs, sagital 7 Graphs, simple 4 7 28 46 64 71 74 76 100 146 151 158 297 308 351 405 409 411 415 Graphs, simple, connected 7 27 46 64 297—298 Graphs, simple, disconnected 27 Graphs, tri-chromatic 100 116 Graphs, unlabelled 405 Graphs, with loops 77 Graphs, without end points 304 Groebner's formula 365 Group actions 393 Group actions, commuting 407 Group actions, isomorphism 394 Group actions, transitive 140 395 Group of rotations of a cube 397 406 Group, alternating 144 321 Group, cyclic 144 321 406 Group, dihedral 144 321 406 Group, symmetric 11 399 H-enriched rooted trees 193 210 229 H-enriched rooted trees, increasing 374—375 Hadamard product 64 65 349 Hanlon's inversion method 305 306 Hayman's theorem 258 Head vertex 62 Heavy rooted trees 224 241 390 Hedges 10 189 Height of a binary tree 238 Hereditary finite sets 338 Hermite polynomials 89 94 184 185 History of increasing rooted trees 383 Homeomorphically irreducible rooted trees 283 Homeomorphically irreducible trees 188 283 291 337 Homogeneous (complete) symmetric functions 88 Hurwitz's inversion formula 184 Husimi graphs 300 Idempotent endofunctions 221 Identity tree 321 Implicit function theorem 192 209 Implicit species theorem 195 Implicit species theorem, multisort species 199 Implicit species theorem, virtual species 212 Increasing binary rooted trees 344 345 359 373 Increasing binary rooted trees, complete 345 358 373 Increasing functions 343 Increasing mobiles 365 391 Increasing ordered rooted trees 365 379 383 Increasing ordered rooted trees with even fibers 381 Increasing ordered rooted trees, m-ary 365 Increasing rooted trees 344 359 367 Increasing rooted trees with even fibers 380 Increasing rooted trees, H-enriched 374—375 Increasing rooted trees, m-ary 365 Increasing rooted trees, plane 363 Increasing rooted trees, planted plane (or planar) 363 Increasing rooted trees, R-enriched 341 361—363 365 371 389 392 Increasing rooted trees, ternary 368 376 380 Indegree 166 Induced order 343 Inj, injections 112 Injective assemblies 332 Injective coloring 324 Injective functions 91 Integral of (weighted) L-species 348 350 Internal vertices 361 Inv, involutions 7 Inventory 81 90 Inverse (multiplicative) 124 Inverse under substitution 130 132 Inversion table 355 Inversions in trees (and rooted trees) 381 Inversions of permutations (lists) 346 Involutions 7 16 89 94 221 251 413 Isomer 288 Isomorphic rooted trees 5 Isomorphism of group actions 394 Isomorphism of L-species 345 Isomorphism of species 21 Isomorphism of structures 3 6 102 Isomorphism of weighted sets 81 Isomorphism type 3 6 14 Isomorphism type, according to sorts 110 Iterated integrals 386 Iterative order 232—234 Jac, Jacobi endofunctions 203 Jacobi endofunctions 172 203 245 Jacobi identity 203 219 Jacobi permutations 374 Jacobi polynomials 172 184 203—205 Jacobi property 203 Joni's multidimensional inversion theorem 221 k-set 101 k-sort 353 k-sort species 102 k-sort species, atomic 158 k-sort species, molecular 155 L, linear orders 7 Labeled structures 12 Labelings 399 Labelings, G-reduced 317 399 Labelings, orderly 366 Lag, Laguerre configurations 95 Lagrange inversion formula 164 174 183 239 Lagrange inversion formula, alternating bidimensional 215 Lagrange inversion formula, weighted version 189 Laguerre configurations 95 213 Laguerre polynomials 95 172 184 214 Laplace — Carson transform 350 Leaf counter 80 Leamer code 355 Leaves 166 181 Left branch 373 Left to right minima 22 Leftist (binary) trees 246 Lemma of R-enriched endofunctions 173 Li — Groebner — Taylor formula 365 Light rooted trees 224 241 390 Limit of a sequence of species 23 Linear (or total) orders, lists 7 10 12 15 50 131 322 346 347 354 356 359 409 411 413 415 417 Linear (or total) orders, lists of length k 37 346 Linear (or total) orders, lists, connected 131 348 Linear (or total) orders, lists, non-empty 57 138 Linear differential equation 377 Linear functional equation 195 Linear Read Bajraktarevic equation 233 Linearization coefficients 95 Lucas numbers 56 Lukasicvich paths 384 Lump of a graph 307 Lyndon words 92 98 m-ary relations 74 76 79 m-ary rooted trees 211 MacMahon's master theorem 217 Major index of a permutation (list) 346 Marked trees 292 Marked trees, rooted 292 Mehler's formula 94 Meir and Moon theorem 260 274 Mixed species 380 Mixed trees 292 Mobiles 240 261 Mobiles, increasing 365 391 Molecular decomposition 141 148 150 226 299 410 421—424 430 431 Molecular decomposition, standard form 142 Molecular k-sort species 155 Molecular species 140 143—147 154—155 311 314 317—318 328 333 418—420 431 432 Molecules, alcohol 287—288 Molecules, alkane 287—288 Moronism of A-weighted sets 81 Morphism of actions 394 Motzkin paths 267 389 Multicardinality 101 Multifunction 101 Multigraphs 114 308 Multiplicable family of species 39 Multiset 101 Multisort L-species 353 Multisort species 102 199 n, 31 Naturality condition 21 Negative part of a virtual species 123 Negative virtual species 123 Negligible 247 Neighbors of vertices 178 Newton — Raphson iteration 222—225 Newton — Raphson iteration for differential equations 389 Newton — Raphson iteration for Read — Bajraktarevic equations 246 Newton — Raphson iteration, higher order 242 Non-separable (or 2-connected) graphs 299—304 Oct, octopuses 12 Octopuses 12 55 56 57 69 221 409 412 415 417 Octopuses, alternating 113 Octopuses, regular 56 Odd alternating permutations 351 359 Odd complete increasing binary rooted trees 359 Odd part of a species 38 410 412 414 416 417 Odd sets 29 348 409 411 415 417 Orbit 395 Ord, order relations 47 Order of a formal power series 264 Order of a graph 297 Order of an unlabelled structure 14 Order of contact 22 23 194 Order relations, partial orders 47 138 Order relations, partial orders, reduced 57 138 Order, induced 343 Order, iterative 232—234 Order, Strahler 235 245 Order, to be of 247 Ordered partitions see “Ballots” Ordered rooted trees 10 167 185—186 190 195 261 284 379 Ordered rooted trees, increasing 363 379 383 Orderly labelling 366 Ordinal product 348 349 Ordinal sum 343 Oriented cycles see “Cyclic permutations” Oriented graphs see “Directed graphs” Oriented rooted trees 285—286 292 Oriented sets 144 152 384 Oriented trees 285—286 292 Otter's formula 277 279 P, polygons 10 Par, set partitions 7 Paraffins 287—288 Parenthesizations 198 379 Parenthesizations, commutative 10 198 222 241 379 410 412 414 Partial differentiation 105 354 Partial orders 47 138 Partial partitions 49 Partitional composition see “Substitution” Partitions see “Set partitions” Permutation representation 394 permutations 7 12 15 31 40 41 45 83 91 99 114 133 139 142 220 251 266 322 346 409 411 413 415 417 Permutations, alternating 344 345 Permutations, alternating, even 351 359 Permutations, alternating, odd 351 359 Permutations, colored 93 Permutations, colored, asymmetric 93 Permutations, compatible 218 Permutations, compatible, connected 219 Permutations, even 144 337 409 411 413 Permutations, Jacobi 374 Permutations, R-enriched 218 Permutations, random 64 Permutations, standard form 22 Permutations, tri-colored 107 Plane trees 178 180 182 190 Plane trees, bicolored 215—217 Plane trees, rooted 168 178 186 190 284 Planted plane (or planar) rooted trees 167 Plethystic substitution 43 84 107 Pointed triangular cacti 305 Pointing, generalized 117 Pointing, species 60 410 412 414 416 418 Pointing, virtual species 125 Pointing, weighted multisort species 106 Pointing, weighted species 84 Polya — Redfield theorem 319 403 POLYGONS 10 30 144 161 297 Polygons, n-gons 30 Polynomial species 111 Polynomials, Bernouilli 268 Polynomials, cycle index 397 Polynomials, Eulerian 355 Polynomials, Hermite 89 94 184 185 Polynomials, Jacobi 172 184 201—205 213 Polynomials, Laguerre 95 172 184 214 Polynomials, tree inversion 297 382 Positive part of virtual species 123 Positive species 123 Power sum symmetric functions 83 333 PQ-trees 24 Preo, preorders 47 Preorders 47 Product of (weighted) L-species 347 Product of A-weighted sets 82 Product of species 32 410 413 414 416 418 Product of virtual species 122 Product of weighted multisort species 104 Product of weighted species 84 Product ordinal 348 349 Pseudo-leftist binary trees 246 Pure simplicial complexes 78 q-analogue 339 347 q-series associated to species 339 Quotient species 147 159 R-enriched, endofunctions 172—173 184 200 218 220 R-enriched, endofunctions, connected 202 R-enriched, endofunctions, partial 172 200 R-enriched, fibers 113 R-enriched, functions 170 R-enriched, permutations 218 R-enriched, rooted trees 165 169 170 181 201 207 224—228 239 260 273 275 281 329 383 410 424—429 R-enriched, rooted trees, unlabelled 263 275 R-enriched, trees 178—182 281 335 410 Radius of convergence 263 Random permutations 64 Random set partitions 63 Random simple graphs 64 Random structures 63 69 Read — Bajraktarevic (functional equation) 230 238 245 Read — Bajraktarevic (functional equation), linear 233 Read — Bajraktarevic (functional equation), Newton — Raphson iteration 246 Recurrent elements 40 86 Red, reduced posets 57 Reduced form of virtual species 122 148 151—152 Reduced order relations (partial orders) 57 138 Regular octopuses 56
Реклама
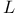-species 
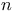as a species 
|
|
О проекте