|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Робертс С. — Динамическое программирование в процессах химической технологии и методы управления |
|
|
 |
| Предметный указатель |
Адаптивные процессы, проверка 464 465
Адаптивные процессы, регулирование скорости истечения из емкости 455
Адаптивные процессы, смена катализатора 459—465
Адаптивные процессы, смена катализатора, класс I 461—463
Адаптивные процессы, смена катализатора, класс II 463 464
Адаптивные процессы, управление по среднему значению 457 458 469 477
Адаптивные процессы, управление с запаздыванием 472 473
Аналитические выражения для функций дохода 215—218
Аппроксимация в пространстве стратегий 19 201—205 248—250 264 363
Аппроксимация в пространстве функций 19 201 202 205—209 264
Аппроксимация квазиоптимальной стратегии 211—214
Атомная энергетическая установка 92—96
Брахистохрона 22 143—146
Брахистохрона вариационное исчисление 143 144
Брахистохрона динамическое программирование 145 146
Брахистохрона сравнение методов решения 161 162
Вариационное исчисление 11 13 21 22 25 97—101 310
Вариационное исчисление и динамическое программирование 97—161
Вариационное исчисление, двухточечная граничная задача 108—110
Вариационное исчисление, затруднения 101
Вариационное исчисление, изопериметрические ограничения 102
Вариационное исчисление, классический метод максимизации 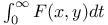 125 126 125 126
Вариационное исчисление, линейность 111
Вариационное исчисление, множитель Лагранжа 103
Вариационное исчисление, негладкие функции 111
Вариационное исчисление, обычный способ определения максимума и минимума 101
Вариационное исчисление, ограничения типа неравенств 103—106
Вариационное исчисление, ограничения типа равенств 102—103
Вариационное исчисление, пример задачи с ограничениями типа неравенств 112 115
Вариационное исчисление, численное решение уравнения ![$f = max[F(c,v)+G(c,v)f_c]$](/math_tex/0bc8591b518cc7078e5e754891ced53082.gif) 128—133 128—133
Вариационные задачи см. "Сглаживание"
Вариационные задачи, подход с точки зрения динамического программирования 115 116
Вариационные задачи, решение методом динамического программирования, максимизация 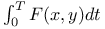 117—121 117—121
Вариационные задачи, решение методом динамического программирования, максимизация 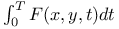 122 124 122 124
Вариационные задачи, решение методом динамического программирования, максимизация 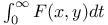 121 122 121 122
Вариационные задачи, решение методом динамического программирования, максимизация дискретного аналога интеграла 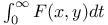 133 134 133 134
Вариационные задачи, решение методом динамического программирования, минимизация дискретного аналога интеграла 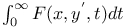 134 135 134 135
Вейерштрасса условие 167
Вогнутая функция 216 217
Выпуклая функция 216 217
Вычислительные аспекты динамического программирования 176—260
Вычислительные аспекты динамического программирования, общая схема вычислений 182—185
Двухточечные граничные задачи 22 см. динамическое
Детерминированные процессы, общая формулировка 438 439
Динамическое программирование см. "Комбинаторный метод"
Динамическое программирование, вариационное исчисление 97—162
Динамическое программирование, вычислительные аспекты 25 26 176—260
Динамическое программирование, двухточечная граничная задача 162
Динамическое программирование, линейность 163
Динамическое программирование, метод решения 20 21
Динамическое программирование, негладкие функции 164
Динамическое программирование, недостатки 23
Динамическое программирование, нелинейное дифференциальное уравнение 116 119—122 124 162 163 243 247
Динамическое программирование, ограничения 163
Динамическое программирование, определение 14
Динамическое программирование, причины применения 177 178
Динамическое программирование, сопоставление с комбинаторным методом 179
Дискретное множество 253—256
Дискретное множество, максимизация 253 254
Дискретное множество, приложение к линейному программированию 254 256
Дискретный процесс 18
Жидкостная экстракция с перекрестным током 64—66
Задачи с начальными условиями 22 см. нелинейное
Замена (регенерация) 25—47 см. "Оборудования "Процесс
Запас на заводе 401—404 410
Запас со стохастическим входом 385—388
Запас, возрастание спроса 427
Запас, дискретная модель 384 385
Запас, закупка товаров на рынке с колеблющимися ценами 388—392
Запас, запаздывание во времени, задача с отсрочкой удовлетворения спроса 428—432
Запас, запаздывание во времени, задача с потерей возможности удовлетворить спрос 429 430
Запас, максимальная прибыль, управление производством и запасами 396—399
Запас, максимальная скорость оборота 400 401 412
Запас, минимальные издержки 412—418
Запас, модель Эрроу — Харриса — Маршака 434
Запас, непрерывная модель 378—379
Запас, непрерывная модель с дополнительными расходами 383 384
Запас, непрерывная модель, числовой пример 383
Запас, простая стратегия при оформлении заказа 425 426
Запас, управление производством и запасами 392—396
Измельчение сетки 185—186 258 335
Изопер и метрическое ограничение 102 103 168 242 244 248 283 284 286 287 290 331 336
Интегральное уравнение 175
Интерполяция 42
Интерцепторное управление 320
Исчисление 13 25
К-я оптимальная стратегия 223—226 227—235 264
К-я оптимальная стратегия, числовой пример 231—235
Катализатора смена (регенерация) 21 26 34—46 см. "Вариационное пример
Катализатора смена, методика расчета для модели II 40—47
Катализатора смена, модель I (простейший случай) 37 38
Катализатора смена, модель II (N-стадийный процесс) 39—47
Катализатора смена, процесс бесконечной длительности 48
Катализатора смена, стратегия 42
Квадратичная аппроксимация 214 215
Комбинаторные задачи 22 23 179
Комбинаторный метод 179 180 225
Компрессор 86
Коэффициент полезного действия цепочки агрегатов 79—81
Коэффициенты разделения 67—71
Критерий качества, квадратичный 341 342 358 359
Лагранжа множитель 17 47 62 66 102 125 126 168 198 199 218—226 244—248 263 272 273 283 285 286 290 292—295 297 334 336
Лагранжа множитель в линейном программировании 258 259
Лагранжа множитель, числовой пример 220—223
Лежандра полином 237—241
Лежандра условие 167
Лежандра — Гаусса формула 236—238
Линеаризация относительно равновесного состояния 338—341
Линейное программирование 23 272 см. приложение
Линейное программирование и динамическое программирование 252—258
Линейное программирование, сокращение размерности 256—258
Линейные приближения, последовательные 248 249
Математическое ожидание 441
Метод характеристик 137—139
Механические квадратуры 235—241
Механические квадратуры и динамическое программирование 238—241
Минимизация максимального отклонения 288 289 320 320
Многореакторная система 55 83 84 263
Многореакторная система параллельных реакторов 56 57
| Многореакторная система последовательных реакторов 59—61
Многореакторная система, распределение питания между реакторами и во времени 62—64
Многостадийные процессы принятия решений 14 15 22
Многостадийные процессы принятия решений с рециркуляцией 362
Многостадийные процессы принятия решений, примеры 14 15 35
Наименьшая сумма 264—266
Наименьшее время 147—161 179—182 308
Нелинейное дифференциальное уравнение см. "Динамическое программирование"
Непрерывные процессы 18
Ньютона — Котеса формула 235 236
Оборудования замена 26 27—34 48—53
Оборудования замена в процессах бесконечной длительности 32—34 48
Оборудования замена с улучшением технологии 49
Оборудования замена, классы 25
Однородность 86 256—260
Оптимальный расчет систем управления 300—304
Оптимальный расчет систем управления, числовой пример 302—304
Периодическая реакция, минимизация времени 147—161
Периодическая реакция, управление по конечному значению 363
Периодическая реакция, числовой пример 152—158
Планирования модель 421 422
Последовательное построение сетки 189—197 см.
Последовательное построение сетки, пример 189—197
Последовательное построение сетки, числовой пример 189—194
Последовательные линейные приближения 248—250
Последовательный анализ 477
Последовательных приближений метод, динамическое программирование 201 202
Последовательных приближений метод, метод Пикара 199—201
Принцип вложения 17 122 126 135
Принцип оптимальности 28 39
Принцип оптимальности, определение 17
Производства расширение 418
Противоточный экстрактор 360 361
Процесс бесконечной длительности 32—34 48
Процесс с бесконечным числом стадий 185 209—211
Размерность большая 23
Размерность многомерная, изопериметрическая задача 226 227
Размерность, двумерные задачи 186 188
Размерность, многомерные задачи 186—188
Размерность, сокращение 24
Размерность, сокращение путем линеаризации, управление по конечному значению 242—248
Размерность, способы решения задач большой размерности 188 194—197
Распределения задачи 58—81 см. "Аппроксимация "Аппроксимация "Коэффициент "Многореакторная "Стохастические "Трубопровод "Химический
Распределения задачи, динамическое программирование и дифференциальное исчисление 197—199
Распределения задачи, характеристика 55
Реактор см. "Периодическая реакция" "Трубчатый
Реактор одиночный 60—61
Реактор, смеситель 358 359 361 363
Регулирование скорости истечения из емкости 322—328 см.
Регулирование скорости истечения из емкости, каскад из двух емкостей 325 326
Регулирование скорости истечения из емкости, каскад из многих емкостей 326 327
Регулирование скорости истечения из емкости, обсуждение 327 328
Регулирование скорости истечения из емкости, одиночная емкость 322 325 365
Рекуррентность 29
Сглаживания задача 268 269 410
Сглаживания задача в вариационном исчислении 139—143
Сглаживания задача квадратичная 405—409
Сетка 40 41 129 131 132 149—151 154 158 178 184 185 186 см. "Последовательное
Симплексный метод 23 272
Складирования задача 271 272 367—378 410 411 419—421
Складирования задача, аналитическое решение 370—376
Складирования задача, решение с помощью динамического программирования 367—370
Складирования задача, решение, числовой пример 376 377
Складирования задача, сравнение решений 377
Состояние системы 15 56 61 438—448
Состояние системы, описание функцией распределения 250—252
Состояние системы, определение 184
Стадии и ступени 15
Стохастические матрицы 450
Стохастические процессы 437—465
Стохастические процессы, задача распределения 444 445 467 468
Стохастические процессы, замена (регенерация) катализатора 445—448 467 468
Стохастические процессы, запаздывание во времени, управление по конечному значению 469—472
Стохастические процессы, общая формулировка 439—442
Стохастические процессы, плотность функции распределения 449—450
Стохастические процессы, регулирование скорости истечения из емкости 451—455
Стохастические процессы, управление по среднему значению 448 449 469 470
Стратегий пространство см. "Аппроксимация в пространстве стратегий"
Стратегия 17 21 33
Стратегия, смена катализатора 35
Тейлора ряды 119 122 123 127
Теплообменники 87 88
Трубопровод жидких продуктов, минимизация затрат на транспортировку 71—79
Трубопровод жидких продуктов, обобщение задачи 76—79
Трубчатый реактор, минимизация максимального отклонения 361 362
Трубчатый реактор, управление по конечному значению 328—335
Трубчатый реактор, управление по среднему значению 335—337
Управление см. "Адаптивные процессы" "Трубчатый
Управление абсорбером с квадратичным критерием качества 348—350
Управление по конечному значению 284—288 307 309—311
Управление по конечному значению, две переменные 286
Управление по конечному значению, линеаризованные уравнения 244—248
Управление по конечному значению, многомерный случай 287
Управление по конечному значению, обобщение 287 288
Управление по среднему значению 276—284 308 309
Управление по среднему значению, общая формулировка 276—278
Управление с запаздыванием 290—295
Управление с квадратичным критерием качества 314—319 342—350 358—359
Управление с обратной связью 276
Управление с помощью вычислительного устройства реактором периодического действия 160
Управление химическим реактором 135—137
Управление, второй метод Кальмана 353—356
Управление, численный расчет, абсорбер с квадратичным критерием качества 350—353
Функциональное уравнение 15
Функциональное уравнение, аддитивная форма 79—81
Функциональное уравнение, мультипликативная форма 81
Функциональное уравнение, числовой пример 92—95
Химический завод с большим числом аппаратов 67—71
Химическое производство см. также "Атомная энергетическая установка" "Катализатора "Компрессор" "Многореакторная "Управление "Химический "Экстракция
Химическое производство, абсорбция 53
Химическое производство, ионообменник 54
Химическое производство, термический трубчатый реактор 53
Числовые примеры см. "Запас непрерывная "Катализатора "К-я "Оптимальный "Последовательное "Последовательных метод
Числовые примеры, замена оборудования 27—29
Числовые примеры, сопоставление комбинаторного метода и метода динамического программирования 179—182
Эйлера — Лагранжа уравнения 22 97—105 108 111 112 114—116 126 168
Эйлера — Лагранжа уравнения, вывод в динамическом программировании 126—128
Экстракция с перекрестным током 64—67 84—86
Эрдмана условия излома экстремалей 105
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



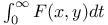
![$f = max[F(c,v)+G(c,v)f_c]$](/math_tex/0bc8591b518cc7078e5e754891ced53082.gif)