|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Garey M.R., Johnson D.S. Ч Computers and intractability. A guide to the theory of NP-completeness |
|
|
 |
| ѕредметный указатель |
Partitioning, variable 255.
PATH CONSTRAINED NETWORK FLOW 215.
Path distinguishes 204.
Path graph, completion 199.
Path graph, restriction to 285.
Path length, total 206.
Path problems 196 203Ч204 211 213Ч214
PATH SYSTEM ACCESSIBILITY 179.
Paths, disjoint 217Ч218.
Paths, Hamiltonian 60 199Ч200.
Paths, longest 75 79 213.
Paths, shortest 79 213Ч214.
Paths, simple 196.
Perfect matchings 194.
Performance guarantees 122Ч151.
Permanent of a matrix 169 252.
Permuiation generation 280.
PERT networks 218.
PET problems 119.
Petri net 279Ч280.
Ph See polynomial hierarchy
Picture compression 232.
PLANAR 3SAT 259.
PLANAR GEOGRAPHY 254.
Planar graphs 195 197
Planar graphs, restriction to 86Ч90 194Ч196 199 204 210 217
PLANAR INDUCED SUBGRAPH 195.
PLANAR SUBGRAPH 197.
POLYLOGSPACE 180Ч181.
Polynomial complete problem 118.
Polynomial hierarchy 161Ч167 171.
Polynomial space completeness 170Ч177.
Polynomial time, algorithm 6Ч11 27.
Polynomial time, approximation scheme 135Ч137.
Polynomial time, DTM program 27.
Polynomial time, isomorphism 160Ч161.
Polynomial time, NDTM program 31.
Polynomial time, reduction 13.
Polynomial time, Turing reduction 111 113Ч117 158.
Polynomial time, verifiability 28 172.
Polynomial transformation 34Ч37 118 120.
Polynomially equivalent languages 37.
Polynomials 249Ч251.
Polynomialty related Length and Max functions 92Ч93.
Polytope non-adjacency 246Ч247.
Post Correspondence Problem 228.
Precedence constrained scheduling 81Ч83 142 144 149 287.
Predicate logic 263.
preemptive scheduling 236Ч237 240Ч242.
Prime attribute (in a relational database) 232Ч233.
Prime numbers 155Ч158 288.
Problem 4.
Processors, different speed 238Ч240.
Processors, identical 238Ч241.
Processors, uniform See different speed.
Processors, unrelated 240.
Product polynomials 250Ч251.
Production planning 243.
Program schemes 275Ч278.
Programmed grammars 270.
Programming (mathematical) 245Ч248.
Programming (mathematical), integer 245.
Programming (mathematical), linear 9 155Ч158 180 215Ч216 287Ч288.
Programming (mathematical), parametric linear 245.
Programming (mathematical), quadratic 245.
Programming (mathematical), zero-one integer 245.
Programs, containment in 277.
Programs, DTM 23Ч26.
Programs, finite memory 275.
Programs, freedom in 277Ч278.
Programs, inequivalence of 275Ч277.
Programs, loop 275Ч276.
Programs, NDTM 30Ч32.
Programs, OTM 111Ч113.
Programs, strong inequivalence of 276Ч277.
Propositional logic 259Ч261.
Provability 262.
Pseudo-polynomial time algorithm 91Ч92 94Ч95 140Ч141 210 223 225Ч227 236Ч238 240 243 249Ч250 252 281.
Pseudo-polynomial transformation 101Ч106.
PSPACE 170Ч178 184.
PSPACE-complete (or hard) problems 254Ч258 265Ч271 275.
PSPACE-completeness See polynomial
QBF See QUANTIFIED BOOLEAN FORMULAS
Quadratic assignment problem 218.
QUADRATIC DIOPHANTINE EQUATIONS 250.
Quadratic programming 245.
QUANTIFIED 3SAT 172 262.
QUANTIFIED BOOLEAN FORMULAS 171Ч172 261Ч262.
Quasi-realtime automata 265Ч266.
Quasi-realtime languages 266 270.
Question 18.
Radius of a graph 205.
Ramsey theory 191.
Randomization tests 281.
Reachability 279.
Reasonable encoding scheme 9Ч10 20Ч23.
Recognition (of a language) 24Ч25 31.
Rectilinear metric 209 219.
Recurrence relations 251.
Recursive language 154.
Reducibility,  - 158Ч159. - 158Ч159.
Reducibility, Cook- 118.
Reducibility, Karp- 118.
Reducibility, many-one 118.
Reducibility, P- 118.
Reducibility, truth-table 164Ч165.
Reducibility, Turing 111Ч113 158.
Reducible graphs, restriction to 192.
Reduction of one problem to another 13Ч14 113Ч117.
Redwood furniture 257.
Register allocation 272Ч273.
REGISTER SUFFICIENCY 272.
REGULAR EXPRESSION NON-UNIVERSALITY 174 267.
Regular expressions 76 174 231 267Ч268.
Regular grammar 269.
Regular graph, restriction to 190 285.
Relational databases 232Ч235.
Relativization 184Ч186.
Resource constrained scheduling 239.
Restriction (proof by) 63Ч66.
Retrieval time 226Ч227.
Reynolds covering 268.
Routing problems 211Ч214.
Safety in databases 234.
Safety in file protection systems 235.
SAT See SATISFIABILITY
Satisfiability 13 107 169 181 259.
SATISFIABILITY OF BOOLEAN EXPRESSIONS 161Ч162
Satisfiability problems 259Ч263
Satisfiability, conjunctive 263.
Satisfiability, generalized 260.
Satisfiability, maximum 259Ч260.
Satisfiability, modal logic 262.
Satisfying truth assignment 38Ч39.
Scheduling See also sequencing.
Scheduling, 3-processor 239 287.
Scheduling, Bow shop 241Ч242.
Scheduling, cyclic 243.
Scheduling, job shop 242.
Scheduling, multiprocessor 65 96 106 238Ч241.
Scheduling, open shop 241.
Scheduling, precedence constrained 81Ч83 144 149 239 287.
Scheduling, preemptive 236Ч237
Scheduling, resource constrained 239
Schemes 276.
| Schemes, B- 277.
Schemes, containment in 277.
Schemes, freedom in 277Ч278.
Schemes, Ianov 276Ч277.
Schemes, inequivalence of 276Ч277.
Schemes, loop-free program 278.
Schemes, program 275Ч278.
Schemes, wtrong inequivalence of 276Ч277.
Search problems 110Ч111 119 167.
Second order logic 264.
Semi-group isomorphism 285.
sequencing 70 73Ч74 96 236Ч238 71 96 102Ч103
Sequential truth assignment 254.
Series-parallel partial orders, restriction to 237.
Set basis 222.
Set covering 53
Set matching 221.
Set PACKING 75 221.
Set panitioning 221.
Set problems 221Ч225.
Set Splitting 76 221.
Shapley Ч Shubik voting power 280.
Shop scheduling 241Ч242.
Shortest circuit 213Ч214.
Shortest common supersequence 228.
Shortest common superstring 228.
Shortest paths 79 213Ч214.
Simple circuits 35 196.
Simple functions 276.
Simple paths 196.
Simultaneous equations 249 251.
Size of a problem instance 5Ч6.
Slack automata 266.
Solvability of equations 250Ч251.
Space complexity 170Ч181.
Space constructive function 182.
Spanning tree parity 287.
Spanning trees 130Ч132 168 206Ч209 287.
Spanning trees, 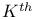 best 208. best 208.
Spanning trees, bounded diameter 206.
Spanning trees, capacitated 206Ч207.
Spanning trees, degree constrained 206.
Spanning trees, directed 208.
Spanning trees, geometric 207 209.
Spanning trees, isomorphic 207.
Spanning trees, maximum leaf 206.
Spanning trees, multiple choice 208.
Spanning trees, optimum communication 207.
Spanning trees, shortest total path length 206.
Sparse matrices 229.
Stacker-crane problem 212Ч213.
Stale minimization for finite automata 266Ч267.
Strong NP-compIeteness See NP-complete in the strong sense
Structured string 21Ч22.
SUBFOREST ISOMORPHISM 105Ч106 202.
Subgraph homeomorphism 285.
Subgraph Isomorphism 18 20 64 104 202.
Subgraph problems 75 193Ч198
Subgraph with property 11 195.
Subgraph, balanced complete bipartite 196.
Subgraph, bipartite 196.
Subgraph, chordal 195.
Subgraph, clique 194Ч195.
Subgraph, comparability 195.
Subgraph, complete See clique.
Subgraph, connected 195Ч198.
Subgraph, cubic 198.
Subgraph, degree-bounded 196.
Subgraph, edge 197.
Subgraph, forest 105Ч106 195 202.
Subgraph, independent 194Ч195.
Subgraph, induced 195Ч197.
Subgraph, isomorphic 193 202.
Subgraph, minimum k-connected 198.
Subgraph, outerplanar 195.
Subgraph, planar 197.
Subgraph, transitive 197.
Subgraph, uniconnected 197.
Subproblem of a decision problem 80Ч90.
Subsequences 228.
SUBSET PRODUCT 224.
SUBSET SUM 223.
substrings 228Ч229 231Ч232.
Subsumption 264.
Supergraph problems 198Ч199.
Supersequences 228.
Superstrings 228.
Tardiness 73Ч74 236Ч237
Tautology 261.
Testing problems 71Ч72
Thickness of a graph 286.
Threshold number of a graph 205.
Tiling 12
Time complexity 6 26
Time constructive function 182Ч183 185.
Timetables 243.
Total graphs, restriction to 195.
Total path length 206.
Total unimodularity 288.
Tournaments, restriction to 213.
Transformation See polynomial transformation
Transitive digraph 197.
Transitive reduction 79 198.
Transitively orientable graphs See comparability graphs.
Traveling salesman 18Ч20 27Ч29 35Ч36 95Ч96 117 211Ч212.
TRAVELING SALESMAN EXTENSION 116Ч117.
Traveling salesman problem 4Ч6 115Ч117 123 128Ч132 139 147
Tree transducers 271.
Trees, restriction to 104 190 198 202 210.
Triangle free graphs, restriction to 193 195Ч196.
Triangle inequality 128Ч129.
Triangulation 218 288.
Tries 226.
Truth assignment 38 261.
Truth functionally complete connectives 261
Truth-table reducibility 164Ч165.
TSE See TRAVELING SALESMAN EXTENSION
Turing machine, deterministic 23Ч27.
Turing machine, nondeterministic 12Ч13 30Ч31.
Turing machine, nondeterministic oracle 161.
Turing machine, oracle 111Ч113 184Ч185.
Turing reduction See polynomial time turing reduction
Turing, A. 12.
Two-commodity network flow 216Ч217.
Unary NP-complete 120.
Unconnected graphs 197.
Undecidable problems 12 245 257 264 269.
UNDIRECTED FLOW WITH LOWER BOUNDS 216.
Unification 252Ч253 264.
Uniform processors See different speed processors.
UNIT RESOLUTION 179.
Universality (of a language) 267 269.
Unrelated processors 240.
Variable partition truth assignment 255.
VC See VERTEX COVER
Vector addition systems 279Ч280.
Vector problems 224Ч225 248 279Ч280.
Vertex cover 46 53Ч56 72 79 85 133Ч134 149 190.
Vertex elimination ordering 201.
Vertex ordering problems 199Ч201.
Vertex substitute 85Ч86.
Voting power 280.
Weighted completion time 237 240Ч241.
X3C See EXACT COVER BY 3-SETS.
Yes-instance 18.
Zero-one integer programming 245.
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -
-  best
best