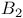Авторизация
Поиск по указателям
Hammer P.L., Rudeanu S. — Boolean methods in operations research and related areas
Обсудите книгу на научном форуме Нашли опечатку?
Название: Boolean methods in operations research and related areasАвторы: Hammer P.L., Rudeanu S. Аннотация: In classical analysis, there is a vast difference between the class of problems that may be handled by means of the methods of calculus and the class of problems requiring combinatorial techniques. With the advent of the digital computer, the distinction begins to blur, and with the increasing emphasis on problems involving optimization over structures, the distinction vanishes.
Язык: Рубрика: Наука /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1968Количество страниц: 329Добавлена в каталог: 08.06.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
174 Absolutely maximal internally stable set 209 218 Absolutely maximal matching 238 Absolutely minimal externally stable set 210 224 Absolutely minimal separating set 242 Acceptable state 295 Adjacency matrix 175 Adjoint of a Boolean matrix 14 Aiidreoli, G. 47 Akers Jr., S.B. 47 Algebraic transitive closure 174 All-integer mathematical programming 159 Analysis of multi-terminals 199 Anghel, D. 280 Angstl, H. 240 Anti-chain 263 Appleby, J.S. 276 ARC 172 Arc-capacity 258 Arithmetic form of a Boolean expression 6 Arnold, B.H. 6 Assignment of numbers to vertices 277 Assignment problems 237 246ff. Balakran 40 Balas, Ј. 49 268 275 276 Balinski, M.L. 48 159 Bantzig,G.B. II 92 170 193 235 248 263 266 278 Barr, M. 47 Basic algorithm for pseudo-Boolean programming 113ff. Basic solution of a pseudo-Boolean inequality 56 Bazilevskil, Ju.Ja. 47 Beale, E.M.L. 48 159 Beaufays, O. 40 Beljinan, R. II IV 48 113 278 Ben — Israel, A. 48 159 Benders, G.F. 48 Berge, C. 2 146 172 209 226 246 Berghiua, J. 270 Bernstein, B.A. 47 Bertier, P. 49 Bipartite graph 237 ff. Birkhoff, G. 47 Blake, D.V. 276 Boole, G. 47 Boolean algebra 6 16 Boolean conjunction (multiplication) 4 16 Boolean determinant 14 Boolean disjunction 2 3 Boolean equation 2 23ff. Boolean expression 7 8 Boolean function 6ff. 24 Boolean function generated by an expression 8 24 Boolean matrix 10ff. Boolean multiplication (conjunction) 3 4 16 Boolean negation 3 16 Boolean ring 20 Bossert, W.H. 276 Breuer, M.A. 288 Burlacu, E. 280 Byser, H.J. 257 Camion, P. 48 40 75ff. 97ff. 109ff. 194 196 197 Canonical form of a linear pseudo-Boolean equation 49 Canonical form of a linear pseudo-Boolean inequality 55 Cardot, C. 286 Caroline, K. 48 Carruccio, E. 40 Cartwright, D. 172—174 Carvallo, M. 6 22 39 40 Catchpole, A.R. 48 Center of a graph 175 Cetkovic, S. 47 Chain in a partially ordered set 263 Characteristic equation 82ff. Characteristic exponent of a Boolean matrix 13 Characteristic function 83 ff. Characteristic vector of a subset 212 228 Charnes, A. 48 151 159 Chromatic decomposition 210 228 Chromatic number 211 Circuit 173 Circulation theorem 262 Closure operator 182 Compatible sets 295 Complete elementary conjunction 9 Complete elementary disjunction 10 Complete graph 174 Conjunctive canonical form of a Boolean function 10 Conjunctive form of a Boolean function 8 Connected graph 174 Constantinescu, P. 100 Converse dominating set 210 Converse domination number 210 Cooper, W.W. 151 Couturat, L. 47 Covering matrix 229 Covering of conjunctions 289 Critical set 244 Csima, J. 276 Culik, K. 40 Cut in a network 1 259 d-externally stable set 224 d-internally stable set 218 De Morgan, A. 38 266 Decomposition matrix of a graph 185 Deficiency of a bipartite graph 244 Del Re, A. 47 Deleanu, A. 277 Denis — Papin, M. 6 83 286 Desbazeille, G. 279 Diameter of a graph 175 Dilworth, A.P. 263 265 Dinkelbach, W. 151 Diophantine equation 194 Discrete variable problems 170 Disjointed form of the characteristic function 95 Disjunctive canonical form of a Boolean function 9 Disjunctive form of a Boolean function 8 Distances in graphs 175 Dixit, A.K. IV Doig, A.G. 48 Dragan, P. IV Dragu§in,C. 199 Dreyfus, S.E. 48 278 Dual of an undirected graph 238 Dubisch, R. 6 Dulmage, A.L. 257 Egervary, J., I 248 Elementary circuit 173 Elementary conjunction 8 Elementary disjunction 8 Elementary path 173 Elngorin, M.Ja. 40 47 Elongation of a vertex 175 Elspas, B. 40 Extension of the basic algorithm for minimization 129ff. Externally stable set 209 220ff. Fabia.i, Cs. IV 109 Family of solutions 45 ff. 55 Faure, R. 6 49 83 286 Fixed variable of a family of solutions 55 Flanient, C. 286 Flegg, H.G. 6 Flood, M.M. 193 Flow in a network 1 258 Ford Jr., L.R. 1 257 258 260 Fortet, R. II 48 75ff. 97ff. 103 113 114 127 194 235 268 270 Four-colour|ng problem 234ff. Fractional pseudo-Boolean programming 151 ff. Fragmentary Hamiltonian circuit 195 Free Boolean algebra 198 Free incidence matrix 199 Free unitary incidence matrix 199 Fridshall, R. 289 Fulkerson, D.R. 1 193 257 258 260 232—264 266 267 Gale, D. 261 Gaspar, T. IV 280 General solution of a Boolean equation 34 Generalized pseudo-Boolean programming 301 ff. Ghouila — Houri, A. 172 Gill, A. 294 Global minimum of a pseudo-Boolean function 102 Globally minimizing point of a pseudo-Boolean function 102 Gomory, R.E. 160 235 Goodman, A.W. 47 Goodstein, R.L. 47 Gotham, A. 289 Gotlieb, C.C. 276 Goto, M. 40 47 298 Graph 172 GrebenScikov, V.N. 32 Greniewski, H. 286 Grigorian, Ju.I. 40 Hakimi, S.L. 224 Hall Jr., M. 257 Hall, P. 246 254 257 Halmos, P.R. 257 Hamiltonian circuit 173 Hamiltonian path 173 Hammer (Ivanescu), P.L. 1 48 82 83 102ff. 113 227 229 233 235 249 258 265 277 288 Harary,F. 172—174 Harmon, H.B. 276 Harper, L.H. 277 278 Healy Jr., W.C. 48 Hoffman, A.J. 257 262 263 265 266 Hungarian method for the transportation problem 248 Idempotent matrix 14 Ihde, G.-B. II Implicant of a Boolean function 288 Inagaki,Y. II 287 298 299 Incidence matrix 175 Independence number 209 Independent set 209 Integer mathematical programming 159 Internally stable set 209 212ff. Interpolation formula 10 22 Irredundant solution of a Boolean equation 35ff. Irredundant solution of the characteristic equation 93ff. Itoh, M. 40 47 Ivanescu, P.L. see “Hammer (Ivanescu) P.L.” Jevons, S. 47 Johnson, S.M. 193 Johnson, W.W. 47 Juncosa, M.L. 289 k-distinguishable sets 295 Karp, R.M. 193 Kaufmann, A. 6 172 189 192 286 Kernel 210 225 Kirchgassner, K. 276 Klir, J. 40 Knapsack problem 278 Koegst, M. IV Komamiya, Y. 47 Konig, D. 172 246 267 Krai, J. II 299 300 Kuhn, H.W. 248 257 Kuiken, C. 48 Kunzi,H.P. IV 159 Kuratowski, K. 182 Lagrangean multipliers 122ff. 141 Lalan, V. 40 47 Land, A.H. 48 Latin matrix 189 Latin multiplication 188 Latin product 188 189 Ledley, R.S. 40 Length of a path 173 Leontieff, W.W. 286 LGwenheim, L. 23 38 39 47 Lindsey, J.H. 278 Linear (continuous) programming 164ff. Linear pseudo-Boolean equation 49ff. Linear pseudo-Boolean inequality 54ff. Linear pseudo-Boolean programming, accelerated 106 Little, J.D.C. 48 Local minimum of a pseudo-Boolean function 135 Locally minimizing point of a pseudo-Boolean function 135 Location of plants 282 Loop 173 Lower bounds on arc flows 260 Lunc, A.G. 13 14 199 287 Lupulescu, M. 280 MaciSSak,K. 151 Maghout,K. 159 164 169 176 204 212 214 220 221 Maitra, K.K. 40 Malgrange, Y. 49 83 189 217 Malstrova, T.L. 288 Mann, H.B. 257 Manne, A.S. 282 283 Marcus, S. 215 Martelotta, R. 47 Martos, B. 151 Matching of a graph 237 Maximal anti-chain 265 Maximal clique of a graph 147 Maximal flow 258 259 Maximal internally stable set 146 209 Maximal matching 238 McCluskey Jr., E.C. 212 277 288 290 293 295 Mealy, G. 294 Median, S. 294 Mendelsohn, N.S. 257 Method of bifurcations 39 ff. Mihoc, Gh. 268 275 Minimal chromatic decomposition 211 Minimal cut 259 Minimal decomposition into chains 263 Minimal externally stable set 146 210 Minimal separating set 242 Minimax of a pseudo-Boolean function 148 ff. Minimization of a Boolean function 287ff. Minimization of a pseudo-Boolean function 102ff. Minimization of the number of states 294ff. Minimum of a pseudo-Boolean function 102 Mititelu, St. 199 Mixed integer-continuous mathematical programming 162ff. Moisil, Gr.C. IV 7 199 293 294 301 Morgenstern, O. 2 Murty, K.G. 48 Murty, U.S.R. II 258 Nadler, M. 40 Near-minima of a pseudo-Boolean function 147 Nemeti,L. 92 Network 258 Newman, E.A. 276 Nghiem, Ph.T. 49 Node 172 Nonlinear pseudo-Boolean equations and inequalities 82 ff. Nordio, S. 40 Norman, R.Z. 172—174 North, J.H. 289 Number of external stability 210 224 Number of internal stability 209 218 Oettli,W. 159 Operations with Boolean matrices 10 Ordering of 10 Ordering of a Boolean algebra 18 Ore, O. 172 209 245 246 257 Parametric solution of a Boolean equation 33ff. 47 Parker, W.L. 47 Partial order 19
Реклама
 |
|
О проекте
|
|
О проекте



 -closure
-closure