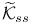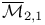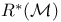Авторизация
Поиск по указателям
Харрис Дж., Моррисон Я. — Модули кривых. Вводный курс
Обсудите книгу на научном форуме Нашли опечатку?
Название: Модули кривых. Вводный курсАвторы: Харрис Дж., Моррисон Я. Аннотация: Изучение геометрии пространства модулей кривых — одно из наиболее активно развивающихся направлений алгебраической геометрии. Книга известных американских математиков содержит доступное для студентов изложение главных результатов в этой области, которые ранее можно было найти только в журнальных публикациях (многообразия Севери, пространства Гурвица, теоремы Харера, теорема Виттена-Концевича, теорема Гротендика-Римана-Роха, теорема Брилля-Нетера, теорема Гизекера-Петри). В ней содержится много примеров, которые рассматриваются как с вычислительной, так и с геометрической точки зрения, что облегчает усвоение материала и показывает связь с другими областями математики.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2004Количество страниц: 448Добавлена в каталог: 12.12.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
318 319 194 195 205 265 282 162 264 265 17 117 42 206 206 374 210 211 194 282 204 12 17 92 93 77 282 251 252 196 131 133 46 46 388—406 148 317 126 261 262 264 319 70 76 186 133 133 70 76 205 83 62 82 84 252 252 252 85 25 133 63 59 94 16 331 15 29 115 17 65 282 54 106 254 205 59 54 66 81 74 73 355 74 73 358 360 62 59 65 54 59 69 30 62 140 252 214 214 375 373 223 223 229 68 103 104 68 413 204 202 185 186 201 387 279 75 274 278 278 406 406 409 423 416 69 269 42 64 134 276 292 276 B-мономиальный базис 261 F(Y) 282 k-гоналыюсть 234 n-канонически вложенная кривая 276 O(m) 18 P 17 Абрамович, Дан 192 Алгебра Вирасоро 100 Алгебраическое пространство 13 57 Алуффи, Паоло 178 Арбарелло, Энрико 84 142 Артин, М. 57 118 Аспект, предельной линейной системы 326 Аспект, соотношения 327 Байер, Дэйв 20 Брилль, А. 301 Брилля — Нётера, дивизор 411 Брилля — Нётера, дивизор, выражение через стандартные классы 412 Брилля — Нётера, дивизор, поднятие на пространства 415 Брилля — Нётера, теорема, второе доказательство 329 Брилля — Нётера, теорема, доказательство Гриффитса — Харриса 303 Брилля — Нётера, теорема, доказательство Севери 302 Брилля — Нётера, теорема, о луче 412 Брилля — Нётера, теорема, обобщенная 329 Брилля — Нётера, теорема, первое доказательство 324 Брилля — Нётера, теорема, подход Гизекера 303 Брилля — Нётера, теорема, подход Лазарсфельда 307 Брилля — Нётера, теорема, третье доказательство 343 Брилля — Нётера, число 299 Брилля — Нётера, число, усовершенствованное 328 Бюрноль Жан-Франсуа 73 Вариации Шиффера 118 121 Веер 31 Вейль, Германн 246 Версальность 117 Верхняя полуплоскость Зигеля 63 Весовая фильтрация 261 Весовая фильтрация, нормализованная 270 Весовая фильтрация, порожденная сюръекцией 262 Взвешенный базис 260 Взвешенный базис, совместимый с весовой фильтрацией 261 Вивег, Экхард 17 297 Вистоли, Анжело 116 180 Виттен, Эд 96 102 107 Внутренняя двойная точка 330 Выпуклое многообразие 103 Геометрическая редуктивность 247 Геометрическая теория инвариантов (ГТИ) 65 Геометрическая теория инвариантов (ГТИ), альтернативы 297 Геометрическая теория инвариантов (ГТИ), задачи 243 Геометрическая теория инвариантов (ГТИ), линеаризация 245 Геометрическая теория инвариантов (ГТИ), плоские кривые 254 Геометрическая теория инвариантов (ГТИ), плоские кубики 256 Геометрическая теория инвариантов (ГТИ), стратегия 243 Геометрическая теория инвариантов (ГТИ), упрощающие предположения 243 248 Геометрическая теория инвариантов (ГТИ), факторизация 245 Геометрическая теория инвариантов (ГТИ), факторизация, базисное множество 248 Геометрическая теория инвариантов (ГТИ), факторизация, слои 249 Гизекер, Дэвид 241 265 269 275 299 303 354 Гильберт, Давид 246 247 253 Гиперэллиптическая кривая 74 172 Гиперэллиптическая кривая, описание 206 Гиперэллиптическая кривая, стабильная 214 Гиперэллиптическая кривая, универсальное семейство 57 Гипотеза Виттена в форме КдФ 100 Гипотеза Виттена в форме Ли 101 Гипотеза Ленга 424 Гипотеза о жестких кривых 45 Гипотеза о наклоне 413 Гипотеза о размерности Кодаиры пространства модулей 408 Гипотеза Севери 388 Гипотеза Фабера о структуре кольца 94 Гипотеза Энриквеса — Франчетты 86 Гипотеза, стандартная 83 Готцманн, Г. 20 Гриффитс, Фил 303 Громов, Михаил 107 Гротендик, Александр 17 58 196 Грубое пространство модулей 14 Грубое пространство модулей, единственность 14 Группа Гротендика, векторных расслоений 194 Группа Гротендика, когерентных пучков 194 Группа Пикара нодальной кривой 309 Гурвиц, А. 51 Двойная (двукратная) прямая 28 40 104 Двойная касательная 172 Двойная точка, внутренняя 330 Двойная точка, общая 385 Двойная точка, специальная 385 Двойственность, Гротендика 114 Двойственность, Кодаиры — Серра 112 Двойственный граф 310 Двукратная (двойная) прямая 28 40 104 Делинь, Пьер 68 Деформация 116 Деформация n-го порядка 117 Деформация версальная 117 Деформация кривой с линейным расслоением 123 Деформация отображения 139 Деформация отображения с условиями касания 145 Деформация отображения с фиксированной областью значений 123 Деформация отображения с фиксированной областью определения и областью значений 123 Деформация первого порядка 116 Деформация первого порядка, вариации Шиффера 118 121 Деформация первого порядка, гладкой кривой 118 Деформация первого порядка, двойной точки 129 Деформация первого порядка, каспа 129 Деформация первого порядка, кривой с линейным расслоением 126 Деформация первого порядка, кривой с эффективным дивизором 125 Деформация первого порядка, линейного расслоения на фиксированной кривой 125 Деформация первого порядка, локального полного пересечения 130 Деформация первого порядка, многообразия с особенностями 130 Деформация первого порядка, нодальных кривых 131 Деформация первого порядка, отображения с фиксированной областью значений 127 Деформация первого порядка, отображения с фиксированной областью определения и областью значений 127 Деформация первого порядка, планарной особенности 129 Деформация первого порядка, помеченной кривой 125 Деформация первого порядка, схемы X 25 Деформация первого порядка, точки самокасания 129 Деформация первого порядка, тройной точки 129 Деформация полная 117 Деформация сохраняющая род 124 Деформация трехступенчатая постановка задачи 118 Деформация универсальная 117 Деформация эквисингулярная 124 Деформация, эквивалентность 116 Диас, Стив 79 90 423 Дивизор, Петри 411 Дивизор, приведенный по модулю n 162 Дилатон-уравнение 98 Долгачев, Игорь 408 Допустимое накрытие 229 Допустимое накрытие, приложения 356 Допустимое накрытие, простейшие случаи 223 Допустимое накрытие, псевдо- 235 Допустимое накрытие, свойства 223 Допустимое накрытие, слияние двух точек ветвления, конструкция 230 Допустимое накрытие, слияние двух точек ветвления, наивное описание 223 Допустимое накрытие, существование 229 Допустимое накрытие, топологическое описание 226 Древовидная кривая 329 Дуализирующий пучок 110 Дуализирующий пучок, обильность 112 Дуализирующий пучок, относительный 113 Загир, Дон 85 Задача о модулях 11 Задача о модулях, фиксация 54 Замена базы 160 Замена базы с простым показателем 162 Замена базы с простым показателем, действие на особые слои 163 Зарисский, Оскар 46 124 Идеал, Фиттинга 134 Идеал, Якоби 128 Инварианты, Громова — Виттена 107 Инварианты, конечная порожденность 246 Инварианты, разделение 247 Индекс ветвления 319 Индекс ветвления, формула Плюккера 319 Капоразо, Дючия 69 Кару, Калле 192 297 Касательное пространство к схеме Гильберта 27 Касательные векторы сложение 25 Касп 129 257 259 394 Кастельнуово, Гвидо 41 Кемпф, Джордж 300 326 Класс рациональных дивизоров на пространстве модулей 180 Класс рациональных дивизоров на стеке модулей 180 Класс рациональных дивизоров, ассоциированый с 186 Класс рациональных дивизоров, ассоциированый с гиперповерхностью в 184 Класс, Тодда 196 Класс, Тодда, мультипликативность 196 Класс, Тодда, формула разложения 196 Клебш, А. 73 Клейн, Феликс 51 Кляйман, Стив 300 326
Реклама
 |
|
О проекте
|
|
О проекте



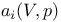
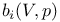
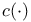
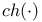
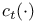
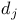

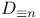
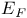
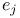
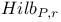
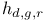
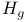
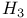 через стандартные классы
через стандартные классы 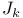
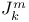
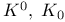
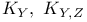
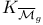 , выражение через стандартные классы
, выражение через стандартные классы 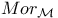
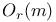
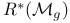
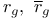
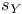
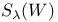
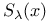
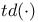
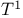
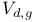
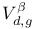
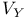
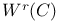 , касательное пространство
, касательное пространство 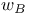
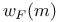
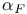
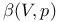

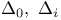
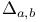

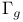
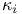

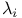
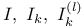
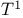
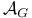
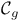
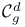
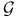
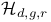
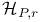

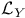
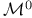
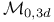 , комбинаторные приложения
, комбинаторные приложения 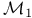
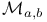
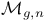
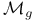
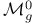
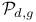
 через стандартные классы
через стандартные классы