Авторизация
Поиск по указателям
Rosenfeld B. — Geometry of Lie Groups
Обсудите книгу на научном форуме Нашли опечатку?
Название: Geometry of Lie GroupsАвтор: Rosenfeld B. Аннотация: This book represents the fruits of the author's many years of research and teaching. The introductory chapter contains the necessary background information from algebra, topology, and geometry of real spaces. Chapter 1 presents more specialized information on associative and nonassociative algebras and on Lie groups and algebras. In Chapters 2 through 6 geometric interpretations of all simple Lie groups of classes An, Bn, Cn, and Dn as well as of finite groups of Lie type are given. In Chapters 5 and 6 geometric interpretations of quasisimple and r-quasisimple Lie groups of the same classes are included. In Chapter 7, for the first time ever, geometric interpretations of all simple and quasisimple Lie groups of exceptional classes G2, F4, E6, E7, and E8 are given. The role of exercises is played by the assertions and theorems given without a full proof, but with the indication that they can be proved analogously to already proved theorems. Audience: The book will be of interest to graduate students and researchers in mathematics and physics.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1997Количество страниц: 393Добавлена в каталог: 18.10.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
160 102 (n + 2) - Spherical coordinates 206 (n — p) - Hedral angle 195 Absolute, bi — Hermitian conic 343 Absolute, complex 311 313 Absolute, differential 17 Absolute, Hermitian conic 335—336 340—341 Absolute, hyperquadric 220—221 223—224 Absolute, null-system 311 313 Absolutes, of quasielliptic, quasihyperbolic etc. spaces 285—286 Absolutes, of r-quasielliptic, r-quasihyperbolic, etc. spaces 292 Absolutes, of symmetric spaces 271 Absorption law 6 Addition of velocities in the Special Relativity 216 Additivity 197 Adjacent lines and points 108 118 Adjoint, group of a Lie group 80 Adjoint, matrix 41 Adjoint, representation 93 Affine, connection 18 Affine, coordinates 7 108 Affine, parameter 19 Affine, rotation 123 Affine, space 7 107 Affine, transformation 26 122 166 Affine, Weyl group 75 Albert theorem 45 56 Albert — Kalish theorem 89 Algebra 4 Algebra, structure 107 Algebraic, complex 152 Algebraic, congruence 152 Almost complex, split complex structure 332 Alternativity 54 Alternion 48 Analytic manifold 15 Analytic point 8 114 Angle between, hypercycles 298 Angle between, hyperspheres 189 Angular defect, excess 197 Annihilator 38 Anticyclic number 35 Antiholomorphic real 2—direction 183 241 339 Antimotion 176 Antisimilitude 176 Antisymmetry axiom 6 Arithmetic Fuchsian group 268 Arm of a couple of vectors 199 Associative law 6 9 Asymptotic direction 136—137 Autodual configuration 155 Automorphism 3 32—33 45—46 Autopolar simplex 147 229 251 296 Axial space 287 322 Basis vectors 4 Beltrami interpretation 232 Betti numbers 85 Bi — Hermitian conic 343 Bialtemion 52 Bicomplex number 34 BICUBE 71 Bioctonion 56 Bioctonionic Hermitian plane 340—341 Biparabolic space 105 Biquasisimple algebra 38 Biquatemion 48 Block 7 Borel subgroup 101 Brauer — Weyl theorem 52 Canonical form of a system of sliding vectors 201 Cartan, algorithm 81 240 Cartan, matrix 68 Cartan, subalgebra, subgroup 62 Cartan, theorem on simple associative algebras 45 Cartan, theorems on exceptional Lie groups 333 340 Cauchy inequality 9 Cauchy — Riemann conditions 33 Cayley number 54 Cayley — Dickson number 55 cell 115 Cellular decomposition, polynomial 115 Center of a hyperquadric 137 296 Center of a hypersphere 10 188 252 Center of a system of sliding vectors 200 CHARACTER 81 circle 11 Circular transformation 204 299 Classification of conics in hyperbolic plane 257—259 Classification of hyperquadrics 259 Clifford algebra, number 48 Clifford quadric 253 Clifford theorems 208—209 Closed subsets, closure 5 Co — Euclidean space 284 Cocube 71 Coefficient of connectedness 75 Collineation 27 125 167 334 Commutative law 6 8 Commutator 23 Comotion 304 Compact space 6 Complete quadrangle, quadrilateral 155 Complex, chain 157 Complex, Lie group 61 71 Complex, number 29 Conformal, configuration 207 Conformal, interpretations of a quadratic space 231 Conformal, space 11 204 Conformal, transformation 27 299 Congruence of m-planes 111 152 Conjugate, diameters 138 Conjugate, elements 29—31 34 40 43 47 49 51 55—56 Connected space 5 Connectedness group 95 Constant, curvature 222 Constant, holomorphic curvature 248 Continuous, mapping 6 Continuous, space 5 Contravariant vector 12 Convolution 12 Coordinates of vectors 4 Copseudo — Euclidean space 284 Correlation 126 Cosymmetry figure 159 304 Couple of vectors 199 Covariant, derivative 16 Covariant, vector (covector) 12 Coxeter, diagram 71—75 Coxeter, number 65 Coxeter, theorem on regular honeycombs in hyperbolic space 267 Coxeter, transformation 72 Cross ratio 127 Cross ratio, pairs 133 cube 71 Cubeable figure 194 Cubic surface with 27 Cubic surface with rectilinear generators 72 151 Curl 14 Curvature of space 219 223 336 Curvature tensor 16 Cyclic number 35 De Vries symbol 155 Derivative of vector function 14 Desargues, configuration 155 Desargues, theorem 110 119 Determinant 41 386 Diameter of hyperquadric 137 Diametral, hyperplane 138 1 Diametral, m-plane 137 Differentiable manifold, vector function 14 Dihedral angle 195 Direct sum, product 3 Discrete space 5 Distance 8 220 Distributive, lattice 6 Distributive, law 8 Divergence 14 Diverging lines 108 Division algebra 4 dodecahedron 71 Dodecahedron, spaces 280—281 Dominant weight 94 Dual, configurations 155 Dual, Lie group 61 Dual, number 31 Duality and stability 328—330 Duality principle 70 135 260 Duocomplex number 34 Duodual number 34 Duooctonion 60 Duoquaternion 48 Dycomplex number 34 Dydual number 34 Dynamical screw 201 Dynkin diagram, theorem 67 Dyoctonion 60 Dyparabolic space 55 Dyquaternion 48 Edge of a polyhedron 184 Eighth-octonion 61 Einstein rule 4 Elastic algebra 91 Elasticity 329 electromagnetic field 217 Ellipsoid 139 Elliptic and hyperbolic, lines of kind a 299 Elliptic and hyperbolic, regular polyhedra 266 Elliptic and hyperbolic, spaces 219 222 Endomorphism 3 Equidistant, barrel 253 Equidistant, hyperquadric 252 254 Equivalent systems of sliding vectors 199 202 Euclidean space 8 168—169 Even-dimensional quadratic symplectic space 313 Event 216 Exponents of a simple Lie group 73 Extended, Dynkin diagram 74 Extended, hyperbolic space 222 225 Extended, pseudoelliptic, pseudohyperbolic space 222 225 Exterior, differential form 20 Exterior, power of a linear representation 96 Exterior, product of vectors 13 Fermi coordinates 235 Field 2 Finite, affine space 161 Finite, conformal space 213 Finite, geometries with exceptional fundamental groups 368 Finite, Hermitian space 282 Finite, projective space 161 Finite, pseudoconformal space 213 Finite, quadratic space 282 Finite, symplectic space 326—327 Flag 103 295 Flag, manifold 103 Flag, plane 32 288 Flag, space 295 Focal variety 111 Free, module 106 Free, vector 198 Freudenthal, algebra 91 Freudenthal, magic square 350 Freudenthal, theorems on metasymplectic geometries 352 366 Frobenius algebra 38 Fuchsian groups 267—268 Fundamental, figures in a space with exceptional fundamental group 356—366 Fundamental, figures in a space with simple fundamental group 102 Fundamental, group 25 Fundamental, linear representations 94 367 Fundamental, root vectors 67 G-elliptic 331 G-pseudoelliptic, G-pseudohyperbolic 332 G-quasielliptic, G-quasihyperbolic etc 333 Galilean space 288 Galois, field 2 Galois, group 69 Gauss — Bonnet theorem 17 General linear group 22 Generalized coordinates, momenta 327 Geodesic 15 Geodesic, curvature 17 Geographical coordinates 193 Gorbunova theorem 305 Gradient 14 Grassmann, algebra 53 Grassmann, coordinates 103 Grassmann, manifold 121 Grassmannian 151 Group, algebra 37 Halfhyperplane, halfline, halfplane, halfpoint 160 Halfspace 160 184 Hamiltonian canonical equations 327 harmonic oscillator 328—329 Hausdorff space 5 Heisenberg group 255—256 313 Hermitian in a finite space 165 Hermitian, conic 354 Hermitian, ellipsoid, hyperboloid, paraboloid 139 Hermitian, elliptic interpretation of projective, symplectic geometry 237 316 Hermitian, Euclidean space 169 Hermitian, form 169 Hermitian, hyperquadric 136 Hermitian, hypersphere 188 Hermitian, linear congruence of lines 114 Hermitian, null-system 153 Hermitian, symplectic space 313 Hesse, configuration 155 Hesse, interpretation 239 Hjelmslev, algebra 38 Hjelmslev, space 109 Holomorphic plane 183 Holomorphy, angle 182 339 Holomorphy, vector 183 339 Homeomorphism 6 Homogeneous space 25 Homomorphism 2 Homothety 27 Hurwitz theorem 40 55 Hyperbolic, Coxeter diagram 268 Hyperbolic, regular polyhedron 266 Hyperbolic, space 219 222 Hypercone 140 Hypercubic 151 Hypercycle 297 Hypercylinder 140 Hyperplane 7 108 Hyperplane at infinity 7 Hyperquadric 136 Hyperquadric in a finite space 163—165 Hyperquartic 151 Hypersphere 10 188 Ibnal — Haytham — Lambert quadrangle 262 icosahedron 71 Ideal 3 Ideal point 11 114 Idempotent 30 Imprimitive group 25 Incidence structure 7 Incident fundamental, parabolic figures 100 Index of a pseudo — Euclidean space 10
Реклама
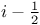— Plane 
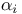-figure, 
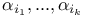-figure 
-space 
|
|
О проекте