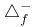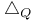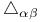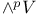|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Woodhouse N.M.J. — Geometric quantization |
|
|
 |
| Предметный указатель |
 1 1
 1 1
 244 244
 247 247
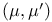 223 223
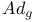 50 50
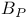 233 233
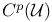 , , 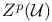 , , 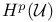 272 272
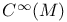 , , 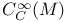 258 258
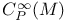 92 269 92 269
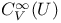 264 264
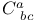 44 44
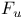 18 18
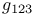 228 228
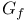 , , 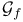 , , 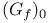 53 53
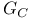 105 105
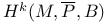 250 250
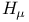 , , 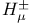 148 148
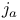 , , 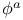 75 75
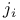 74 74
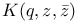 96 96
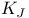 , , 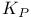 223 223
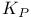 185 185
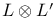 267 267
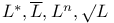 267 267
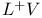 93 93
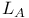 , , 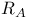 50 50
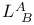 108 108
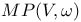 224 224
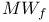 58 58
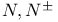 148 148
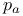 , , 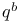 6 19 6 19
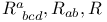 263 263
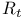 138 138
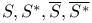 108 108
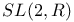 53 53
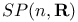 5 5
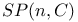 5 5
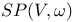 5 5
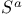 115 115
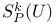 77 92 77 92
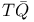 25 25
![$T^{(ab...c)}, T^{[ab...c]}$](/math_tex/6e520e35f91c9a97f23923f9ed074e1682.gif) 257 257
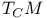 , , 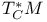 258 258
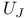 224 224
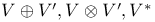 263 263
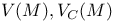 258 258
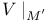 , , 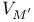 265 265
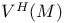 10 10
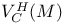 11 11
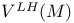 10 10
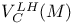 11 11
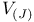 257 257
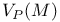 269 269
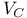 257 257
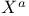 , , 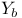 3 3
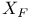 9 9
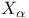 , , 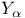 , , 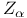 104 104
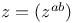 93 93
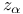 221 221
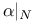 260 260
 268 268
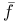 186 251 186 251
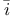 26 26
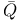 25 25
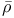 219 219
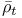 186 186
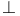 2 2
 242 242
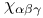 219 219
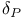 186 232 186 232
 156 156
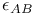 108 108
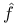 157 162 250 157 162 250
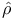 163 163
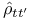 164 164
 199 199
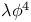 207 207
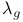 , , 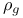 50 50
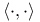 156 162 156 162
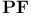 , ,  221 225 221 225
 , ,  244 244
 248 248
 38 38
 104 104
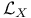 259 259
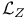 185 185
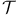 104 104
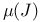 223 223
 67 130 185 67 130 185
 , , 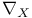 264 264
 6 197 6 197
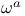 133 133
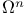 5 5
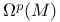 , , 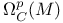 259 259
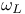 17 17
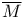 120 120
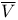 258 258
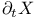 261 261
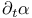 262 262
 212 212
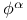 130 130
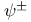 147 147
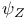 174 174
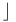 259 259
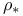 , , 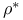 260 260
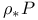 , , 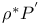 270 270
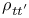 262 262
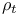 261 261
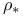 113 113
 200 200
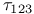 214 214
 , ,  246 246
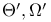 247 247
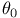 166 166
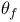 , , 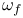 51 51
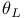 18 18
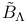 241 241
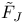 224 224
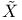 261 261
 , , 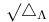 236 236
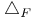 209 209
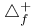 , , 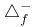 105 105
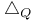 185 185
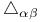 214 214
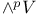 257 257
A 197
Action variables 74 242
Adjoint action 50
Adjoint representation 43
Aharonov — Bohm effect 188
Angle variables 75 242
Anti-unitary operator 165
Anticanonical transformations 56 121 165
Anticommutation relations 216
Antiparticle 120
B 158
Bargmann transform 196
Berry's phase 225 243
Bivectors 111
Bivectors, self-dual 111
BKS construction 202
Bohr — Sommerfeld condition 201
Bohr — Sommerfeld condition, corrected 201 241 249
Borel subgroup 105
Borel — Weil theorem 176
Bosons 176
C 120
Canonical 1-form 6 19
Canonical 2-form 6 19
| Canonical bundle 223
Canonical bundle of a distribution 270
Canonical coordinates 8
Canonical coordinates, adapted to a polarization 71
Canonical diffeomorphism 8 63
Canonical flow 9
Canonical quantization 187
Canonical transformation 62—63
Canonical transformation, linear 5 63
Canonically conjugate variables 15
Caustic singularity 201
Cech cohomology 271
Characteristic distribution 12
Charge conjugation 120
Charge quantization 187
Charged symplectic structure 36 187
Chern class 161
Chern class of a complex manifold 235
Circle action 48
Classical observable 9
Coadjoint action 50 52
Coadjoint orbit 51
Coboundary 271
Coboundary Lie algebra 40
Coboundary operator 271
Cochain 271
Cocycle 271
Cocycle Lie algebra 40
Cocycle of a pairing or embedding 275
Cocycle relations 266
Coherent states 174 178—180
Cohomological wave functions 249
Cohomology group 272
Cohomology group, holomorphic 272
Coisotropic foliation 66
Coisotropic section 100
Coisotropic submanifold 13
Coisotropic subspace 2 4
Compact group 103 176
Complete vector field 261 262
Complex conjugate vector bundle 264
Complex conjugate vector space 258
Complex distribution 269
Complex distribution, integrable 270
Complex manifold 270
Complex structure 257
Complex structure, compatible with  89 89
Complex structure, positive 89
Composite system 57
Configuration space 16
Connection 264
Connection form 268
Constraint 13 28
Constraint Dirac — Bergmann theory 34
Constraint first class 13
Constraint holonomic 28 31
Constraint in a Humiltoian system 31
Constraint instantaneous 30
Constraint nonholonomic 28
Constraint primary 20 34
Constraint quantization 182
Constraint second class 13
Constraint secondary 35
Contraction 259
Cotangent bundle 68 165
Covariant derivative of a spinor 111
CR structure 102
Curvature 265
D, E 66 91
D, L 250
Darboux's theorem 6
De Rham isomorphism 273
density 258
Determinant bundle 223
Differential form time-dependent 262
Differential form type (r, s) 270
Differential form with values in V 264
Dirac equation 149
Direct sum of vector bundles 263
Distribution, integrable 269
Distribution, involutive 269
Distribution, real 269
Distributional wave function 238
Dolbeault isomorphism 274
Dual bundle 263
e 130
Einstein conventions 3
Einstein's equations 143
electromagnetic field 82 134
Elementary systems 49 169
Energy 120
Energy-momentum tensor 140
Equivalence of vector bundles 264
Euclideanization 205
f 220
Feynman expansion 205
Fibre 263
Field 130
Field equation, massless 193
Flag manifold 106
Flag manifold, flat connection 100
Flow of a vector field 261
Flow time-dependent 262
Fock space 173 209
Fock space, fermion 216
Foliation 269
Foliation, reducible 269
Forward tube 255
Four-momentum 114
Fubini — Study metric 95
Fubini — Study symplectic structure 190 235 255
Function constant along P 269
Function locally constant 272
Function time-dependent 262
Galilean group 47
Galilean transformation 36
Gauge transformation 135 157
Generalized momentum 19
Generating function 62
Generating function of a canonical diffeomorphism 63
Geodesic flow 202
Graph of a 1-form 61
Group of transformations 261
H 17
Half-form 224
Half-form bundle 232
Hamilton — Jacobi condition 237
Hamilton — Jacobi equation 60 78
Hamilton — Jacobi equation complete integral 79
Hamilton — Jacobi equation time-dependent form 80
Hamilton's equation 10
Hamilton's principle 17
Hamilton's two-point characteristic function 64 81
Hamiltonian 9 17 39 140
Hamiltonian action 39
Hamiltonian action, quantized 169
Hamiltonian completely integrable 75
Hamiltonian interaction 207
Hamiltonian time-dependent 13
Hamiltonian vector field 9
Hamiltonian vector field, complex 11
Hamiltonian vector field, time-dependent 14
Hannay's angles 243
harmonic oscillator 175 181 225 243
Heisenberg group 166 174 224
Heisenberg picture 21
Helicity 115
Hermitian structure 264
Hermitian structure, compatible with  264 264
Highest wight orbit 177
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



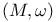
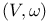
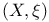
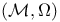
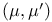
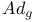
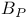
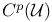 ,
, 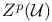 ,
, 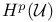
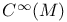 ,
, 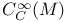
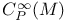
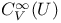
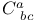
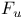
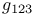
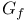 ,
, 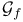 ,
, 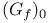
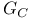
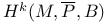
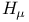 ,
, 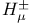
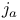 ,
, 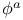
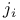
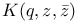
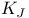 ,
, 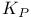
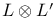
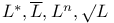
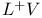
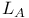 ,
, 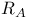
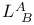
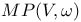
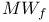
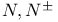
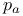 ,
, 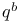
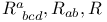
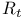
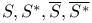
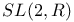
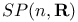
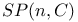
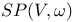
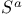
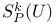
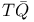
![$T^{(ab...c)}, T^{[ab...c]}$](/math_tex/6e520e35f91c9a97f23923f9ed074e1682.gif)
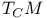 ,
, 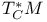
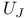
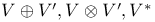
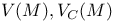
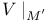 ,
, 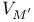
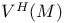
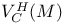
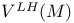
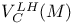
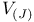
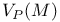
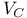
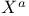 ,
, 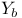
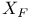
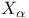 ,
, 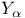 ,
, 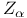
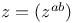
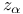
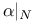

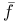
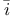
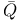
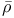
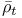
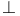

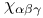
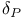

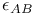
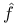
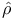
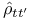

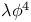
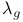 ,
, 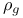
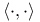
 ,
, 
 ,
, 
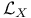
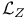
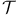
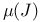

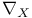

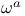
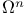
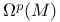 ,
, 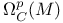
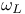
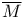
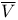
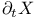
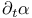

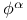
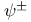
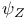
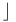
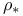 ,
, 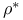
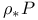 ,
, 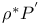
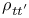
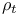
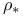

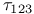
 ,
, 
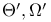
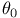
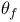 ,
, 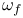
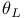
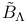
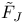
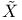
 ,
, 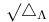
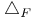
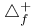 ,
,