|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wagner M. — Unitery Transformations in Solid State Physics |
|
|
 |
| Предметный указатель |
Soft mode 143
Sommerfeld, A. 197
Sondheimer, E.H. 166 167 S.”)
Spectral function 167
Spin transformations 34ff
Spin-phonon Hamiltonian 108
Spin—1 transformation 330(t)
Static approach 205 210
Static base 336(t)
Stevens transformation 201
Stevens, K.W. 196 201
Stinchcombe, R.B. 130 131 165
Stoneham, A.M. 202 209
Straley, J.P. 149
Successive unitary transformations 96ff 238(t) 239(t)
Superconductivity 161ff 183
Tables of unitary transformations 231—336(t)
Tables of unitary transformations, coupled oscillators, b-b+ representation 284—293(t)
Tables of unitary transformations, coupled oscillators, P-Q representation 270—283(t)
Tables of unitary transformations, coupled spins (coupled two-level systems) 294—299(t)
Tables of unitary transformations, general formulae 231—240(t)
Tables of unitary transformations, miscellaneous transformations 319—336(t)
Tables of unitary transformations, oscillator-spin transformations 300—318(t)
Tables of unitary transformations, single oscillator transformations, b-b+ representation 251—256(t)
Tables of unitary transformations, single oscillator transformations, P-Q representation 241—251 (t)
Tables of unitary transformations, single spin-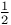 transformations 257—262(t) transformations 257—262(t)
Tables of unitary transformations, two-level transformations 263—269(t)
Tani, S. 102 315
Test-Hamiltonian 6 70 71 74 79 80 222
Thermal Hartree — Fock approximation 216
| Three-level transformation 331 ff(t)
Time-dependent unitary transformations 222ff 234(t) 235(t)
Toyozawa, Y. 129
Transverse field in spin system 258(t) 259(t)
Tunneling problem, phonon assisted 110
Two-level transformations 39ff
Two-site problem 125
Valatin, J.G. 43 162
Variational Principle 77 78 79
Variational principle for excited states 2 75ff
Variational procedures 70ff
Vibronic problem 108ff 121 133 224ff
Vibronic systems 334(t)
Von Neumann — Wigner mechanism 208
Wagner, M. 11 12 39 77 85 109 111 114 115 116 119 123 124 133 136 137 147 149 150 152 153 156 163 173 180 181 182 183 184 203 206 211 212 228 230 318 334 335 W.E.” “Briihl S.” “Denner V.” “Junker W.” “Kuhn W.” “Nusser H.” “Perlin Yu.E.” “Rueff M.” “Sigmund E.”)
Wannier bases, displaced 196ff
Wannier functions 2 201
Weaver, D.L. 330
Wei, J. 105
Weiss, G.H. 68 96 150 152 153 A.A.”)
Wentzel, G. 1
Wenzel, G. 142 149
Whitfield, G.D. 125 156 196 197 198 199 C.G.”)
Wick's theorem 166 186
Wilcox, R.M. 90 99 100 104 105
Williams, H.C.W.L. 149 (see also “Moore M.A.”)
Yamazaki, K. 31 79 H.”)
Zassenhaus formula 99f
Zeks, B. 142 (see also “Blinc R.”)
Zienau, S. 156 (see also “Frohlich H.”)
Zubarev, D.N. 130 131 132 165 167
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



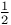 transformations
transformations