|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Baker G.A. Ч Essentials of Padé Approximants in Theoretical Physics |
|
|
 |
| ѕредметный указатель |
Acceleration of convergence of sequence 108Ч109
ArmsТ and EdreiТs theorem 257Ч259
Baker Ч Gammel Ч Wills conjecture 188Ч189
BakerТs corollary 181
BeardonТs theorem 184Ч185
BeardonТs theorem for [L/1] 156
BernsteinТs Theorem 266
Bessel function 70Ч71
Bigradients 58 61
Bounds to averages 250Ч251
Bounds to averages on distribution functions 248Ч251
Capacity 192
CarlemanТs inequality 227Ч228
CarlemanТs theorem 224Ч225
CartanТs lemma 174Ч175 194Ч195
Coefficients of Pade approximants, calculation of 77Ч79
Compact expression for Pade approximants 36
Continued fractions 42Ч64
Continued fractions, associated type 56
Continued fractions, convergence theorems 47Ч55
Continued fractions, corresponding type 56
Continued fractions, equivalence transformations 44Ч46
Continued fractions, equivalent type 57
Continued fractions, Euler-type 57
Continued fractions, Euler-type, even part of 45
Continued fractions, GaussТs continued fraction 62Ч64
Continued fractions, general corresponding type 61
Continued fractions, Jacobi-type 56
Continued fractions, odd part of 45
Continued fractions, Pade approximants, relation to 57Ч58
Continued fractions, recursion formulas, fundamental 42Ч44
Continued fractions, Stieltjes-type 56
Continued fractions, Taylor series, relation to 55Ч57
Convergence in Hausdorff measure 193Ч205
Convergence in Hausdorff measure, convergence theorems 197Ч203
Convergence in Hausdorff measure, error formula 195Ч196
Convergence in Hausdorff measure, examples of 204Ч205
Convergence in the mean on Riemann sphere 203
Convergence of general sequences 166Ч185
Convergence of general sequences, approximant pole locations 175Ч180
Convergence of horizontal sequences (see Convergence of vertical sequences Duality
Convergence of vertical sequences 133 165
Convergence of vertical sequences, functions with only polar singularities 134Ч143
Convergence of vertical sequences, functions with polar singularities and УsmoothФ nonpolar singularity 143 147
Convergence of vertical sequences, functions with several УsmoothФ boundary circle singularities 147Ч149
Convergence of vertical sequences, general entire functions 155
Convergence of vertical sequences, N-point Pade approximant, extension to the 160Ч165
Convergence of vertical sequences, nonvertical sequences, extension to some 154Ч155
Convergence of vertical sequences, УsmoothФ entire functions 149Ч154
Convergence theory 119Ч205
Convergence uniqueness theorems 170
Convergent 43
Critical phenomena 10 12 274Ч279
Critical phenomena, bounds on thermodynamic limit 279
Critical phenomena, errors in, structure of 277Ч279
Critical phenomena, magnetic susceptibility 10 12
DeMontessus de BalloreТs theorem 134
Determinantal solutions for Pade approximants 8Ч9
Discovery of Pade approximants 7
Disk problem 183
Distribution of poles and zeros 186Ч192
Divergence series (see GaussТs hypergeometric function Stieltjes series
Duality theorem 112Ч113
Duality theorem, matrix Pade approximants 271
Duality theorem, multivariate approximants 293
electrical circuits 288Ч291
Epsilon algorithm 75
Error formula for Pade approximants 195Ч196
Error function 73
EulerТs divergent series 76 212 216Ч217
Existence theorem 24Ч25
Exponential function, Pade approximants to 11
Exponential integral 73
Gammel-Baker approximants (see Generalized Pade approximants)
GammelТs example 204Ч205
GaussТs hypergeometric function 62Ч73
GaussТs hypergeometric function, Bessel functions as confluence of 70Ч71
GaussТs hypergeometric function, confluent form of 68Ч70
GaussТs hypergeometric function, continued fraction for ratio of 62Ч64
GaussТs hypergeometric function, divergent series 71Ч73
GaussТs hypergeometric function, special cases of 64Ч68
Generalized Pade approximants 263Ч266
Geometric-mean-arithmetic-mean inequality 227Ч228
Hamburger problem, convergence 23
Hamburger problem, inclusion regions 246Ч248
Hamburger problem, scattering physics and 281Ч284
Hausdorff measure (see Convergence in Hausdorff measure)
Hermite polynomials (see Orthogonal polynomials)
HermiteТs formula 160
identities 26Ч41
Identities, cross ratio 28Ч30
Identities, expressed with Pade coefficients 34Ч36
Identities, five-term 33Ч34
Identities, three-term 30Ч33
Identities, triangle 31
Identities, two-term 26Ч28
Inequalities, fundamental 52
Infinite coefficients, series with, approximation of 267Ч269
Invariance properties 5 110Ч117
Invariance properties, argument transformations 110Ч111
Invariance properties, value transformations 112Ч113
Invariance Theorem 113
Invariance theorem, approximants, for 271Ч272
Invariance theorem, matrix Pad 6
Jost function 284
Kirchhoffs rules 289
Lagrange interpolation formula generalized 101
Lagrange Ч Beltrami decomposition 91
Laguerre polynomials (see Orthogonal polynomials)
Laplace transforms, inversion of 292
Legendre polynomial expansions, approximants for 291
Legendre polynomials (see Orthogonal polynomials)
LeRoy functions 266
| Linear fractional group 113Ч117
Linear fractional group, rotations of Riemann sphere equivalent to 115Ч117
Location of cuts 189Ч192
Location of cuts, numerical examples 128Ч131
Mandelstam representation 285Ч286
Matrix Pade approximants 270Ч273
Measure, convergence in (see Convergence in Hausdorff measure)
Moment problem 85
Moment problem, trigonometric 93
MontessusТs theorem 134Ч143
Multiple angle formulas (see Orthogonal polynomials)
Multivariate approximants 292Ч293
N-point Pade approximant 100Ч109
N-point Pade approximant, 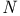 th roots of unity, fit on 107Ч108 th roots of unity, fit on 107Ч108
N-point Pade approximant, Cauchy Ч Jacobi problem 101 105Ч106
N-point Pade approximant, convergence of vertical sequences 160Ч165
N-point Pade approximant, determinantal solution 103
N-point Pade approximant, inclusion regions 244Ч246
N-point Pade approximant, orthogonality property of denominators 106
N-point Pade approximant, Pade problem as a special case 100Ч101
Noncommunative algebra, Pade approximants over (see Matrix Pade approximants)
Normal, definition of 24
Notation for Pade approximants 7
Numerical examples 121Ч132
Numerical examples, asymptotic series, behavior for 127Ч128
Numerical examples, convergence at regular points 121Ч123
Numerical examples, convergence at singular points 123Ч126
Numerical examples, location of cuts 128Ч131
Orthogonal polynomials 85Ч89
Orthogonal polynomials, extremal properties 89
Orthogonal polynomials, Hermite polynomials 88
Orthogonal polynomials, Laguerre polynomials 87
Orthogonal polynomials, Legendre polynomials 87
Orthogonal polynomials, multiple angle formulas 88
Pade denominators, orthogonality properties of 85Ч86
Pade table 7 9Ч10 13Ч25
Pade table, block structure 19Ч24
Pade table, C table 13Ч19
Pade table, computation of 75Ч76
Pade table, connection between Pade tables of  and and  38Ч41 38Ч41
Pade table, GraggТs example 23
Pade table, SylvesterТs determinant identity 14Ч16
Pade table, Taylor series 9
Pade Ч Borel summation procedure 287
PadeТs block theorem 20Ч22
PadeТs block theorem, illustration of 22
Parabola theorem 51Ч54
Polya freqeuency series 252Ч260
Polya freqeuency series, characterization of 253Ч255
Polya freqeuency series, convergence properties 255Ч260
Quadratic form, decomposition of into a sum of squares 90
Quadratic form, eigenvalue distribution for 93Ч99
Quadratic form, Toeplitz 93
Quantum field theory 286Ч287
Quotient difference algorithm 80Ч84
Quotient difference algorithm, rhombus rules 81
Recursion relations 74Ч84
Recursion relations, BakerТs algorithm 77Ч78
Recursion relations, coefficient problem 77Ч79
Recursion relations, root problem 80Ч84
Recursion relations, value problem 75Ч76
Recursion relations, WatsonТs algorithm 79
Riemann sphere 113Ч117
Riemann sphere, chord length 117
Riemann sphere, complex plane, spherical representation of 114Ч115
Riemann sphere, continuity on 166
Riemann sphere, convergence in the mean on 203
Riemann sphere, convergence on 133Ч134
Riemann sphere, equicontinuity on 167
Riemann sphere, rotation as linear fractional transformation 115Ч117
Root solving, acceleration procedure for 292
Saffs theorem 163Ч165
Scattering physics 280Ч287
Scattering physics, forward scattering amplitude 281Ч282
Scattering physics, partial waves 282Ч284
Scattering physics, potential scattering 280Ч285
SchwarzТs lemma 173Ч174
Series with infinite coefficients, approximation of 267Ч269
Special functions, calculational procedures 292
Stieltjes expansion theorem 91
Stieltjes for N-point problem 244Ч246
Stieltjes integral representation 229Ч230
Stieltjes representation theorem 230
Stieltjes, convergence 218Ч233
Stieltjes, definition 209Ч213
Stieltjes, determinantal conditions 210Ч213
Stieltjes, diagonal sequences, limit of, existence 218Ч219
Stieltjes, dynamic dipole polarizability 291
Stieltjes, Hamburger problem 230Ч233 246Ч248
Stieltjes, inclusion region(s) for value of approximants 234Ч248
Stieltjes, inequalities 213Ч217
Stieltjes, interlacing properties 213Ч214
Stieltjes, Pade approximant coefficients to series coefficients relation 220
Stieltjes, scattering physics and 285
Stieltjes, series of 207Ч251
Stieltjes, uniqueness, conditions for 219Ч228
Taylor series 3Ч4
Taylor series, continued fractions and 55Ч57
Taylor series, expansion, definition of Pade approximants from 4Ч8
Taylor series, Pade table 9
Taylor series, values of function and 3Ч4
ThieleТs reciprocal difference method 105 106
Three-body problem 286
Transfinite diameter 192
TschebycheffТs inequalities 248Ч251
Two-variable approximants 292Ч293
Uniqueness theorem 8
Unitary, of matrix Pade approximant 273
VillaniТs limit theorem 268
WallinТs corollary 154Ч155
WallinТs example 204Ч205
WalshТs corollary 181
WilsonТs Theorem 143Ч147
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



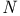 th roots of unity, fit on
th roots of unity, fit on  and
and 