|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Mickens R.E. Ч Mathematical Methods for the Natural and Engineering Sciences |
|
|
 |
| ѕредметный указатель |
Airy equation 269 292Ч293
Asymptotics, asymptotic sequences 497
Asymptotics, elementary operations on asymptotic sequences 499Ч501
Asymptotics, expansions 497Ч498 410Ч412
Asymptotics, gauge functions 495
Asymptotics, generalized asymptotic series 503
Asymptotics, integration by parts 413Ч416
Asymptotics, Laplace's theorem for integrals 218
Asymptotics, order symbols, "o" and "O" 495Ч497
Asymptotics, Watson's lemma 417Ч418
Averaging method, perturbations, derivation 367Ч369
Averaging method, perturbations, procedure 369Ч370
Averaging method, perturbations, stability of limit-cycles 272
Averaging method, perturbations, two special cases 370Ч371
Averaging method, perturbations, worked examples 373Ч376
Averaging, difference equations 394Ч396
Averaging, worked examples 396Ч399
Bernoulli functions 423Ч425
Bernoulli functions, differential equation 426
Bernoulli numbers 425
Bessel equation 293Ч296
Bessel functions, general, asymptotic representations 324
Bessel functions, general, equations reducible to 348Ч350
Bessel functions, general, generating function 323
Bessel functions, general, integral representations 324
Bessel functions, general, Rodrique type formula 323
Bessel functions, general, series representation 322
Bessel functions, special types, Hankel functions 324
Bessel functions, special types, modified Bessel functions 325 326
Beta function, definition 71 72
Beta function, properties 88
Bifurcations, blue sky phenomena 181
Bifurcations, Hopf 184Ч186
Bifurcations, point 180
Boltzmann problem 464Ч467
Casorati (determinant) 221 223
Center 135 143 144
Center, second derivative test 178
Characteristic equation 231
Characteristic scales 4Ч6
Chebyshev polynomials 246Ч248
Clairaut's equation 241Ч242
Convolution theorems, Fourier transform 48Ч49
Convolution theorems, Laplace transform 55
Cosine integral 421Ч423
Delta function, Dirac 57 276Ч277 284 330Ч331
Delta Function, Dirac, definition 76Ч77
Delta Function, Dirac, derivative 80
Delta Function, Dirac, higher dimensions representations 80Ч81
Delta Function, Dirac, properties 77Ч80
DeMoivre's theorem 21
Determinants, special, Hessian 488
Determinants, special, Jacobian 487
Determinants, special, Wronskian 488
Detonation problem 464Ч467
Difference equations, 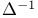 206Ч209 206Ч209
Difference equations, definition 200
Difference equations, existence theorem 200
Difference equations, first-order (linear), form 215
Difference equations, first-order (linear), general solution 216
Difference equations, first-order (linear), homogeneous equation 215
Difference equations, first-order (linear), inhomogeneous equation 215
Difference equations, fundamental operators, E and A 202Ч203 204Ч205
Difference equations, general order (linear), existence and uniqueness theorem 221
Difference equations, general order (linear), fundamental theorems, homogeneous equations 222
Difference equations, general order (linear), homogeneous equation 220
Difference equations, general order (linear), inhomogeneous equation 220
Difference equations, general order (linear), inhomogeneous equation, solutions 223Ч224
Difference equations, genesis 197Ч200
Difference equations, linear, constant coefficients, characteristic equation 231
Difference equations, linear, constant coefficients, homogeneous equation 231
Difference equations, linear, constant coefficients, homogeneous equation, solutions 231Ч232
Difference equations, linear, constant coefficients, inhomogeneous equation 231
Difference equations, linear, constant coefficients, inhomogeneous equation, solutions 232Ч234
Difference equations, linear, nonlinear 201
Difference equations, nonlinear, Clairaut's equation 241Ч242
Difference equations, nonlinear, homogeneous 239
Difference equations, nonlinear, miscellaneous forms 242Ч243
Difference equations, nonlinear, Riccati equations 239Ч241
Difference equations, order 200
Difference equations, properties 205Ч206
Difference equations, uniqueness theorem 200
Differential equations, asymptotics of solutions, Airy equation 292Ч293
Differential equations, asymptotics of solutions, Bessel equation 293Ч296
Differential equations, asymptotics of solutions, elimination of first-derivative terms 287Ч288
Differential equations, asymptotics of solutions, general expansion procedure 296Ч298
Differential equations, asymptotics of solutions, Liouville Ч Green transformation 290Ч292
Differentiation of a definite integral 485
Diffusion equation 49Ч51 462Ч464
Dimensionless variables 4Ч6
Dirichlet integrals, definitions 82
Dirichlet integrals, expressed as gamma functions 83 84
Eigenfunctions 270Ч271
Eigenfunctions, completeness relation 273
Eigenfunctions, expansion of functions 272
Eigenfunctions, orthogonality 271
Eigenvalues 270Ч271
Eigenvalues of 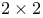 matrix 485Ч486 matrix 485Ч486
Eigenvalues, reality of 277Ч278
Electron, magnetic moment 91
Elliptic functions, definitions 100
Elliptic functions, Fourier expansions 103Ч104
Elliptic functions, properties 100Ч103
Elliptic integrals, first kind 98
Elliptic integrals, second kind 98
Euler Ч Maclaurin sum formula 426Ч427
Euler Ч Maclaurin sum formula, worked examples 427Ч431
Euler's formula 21
Even function 26Ч28
Exponential order 53
Factorial functions 212Ч215
Family of a function 233
Fermi Ч Dirac integrals 89 90
First integral 132 133Ч134 177
Fisher equation, definition 448
Fisher equation, fixed-points 449
Fisher equation, initial conditions 448
Fisher equation, perturbation solution 453Ч455
Fisher equation, traveling wave solution 448Ч449
Fisher equation, velocity restrictions, traveling waves 449
Fixed points, classification 143
Fixed points, definition 116 132
Fixed points, stability 122Ч124
Fourier series 28Ч33
Fourier series, convergent properties 31
Fourier series, cosine 30
Fourier series, definition 29Ч30
Fourier series, differentiation 32Ч33
Fourier series, integration 32
Fourier series, Parseval's identity 33Ч34
Fourier series, sine 30
Fourier series, square integrable 32
Fourier transforms, convolution theorem 48Ч49
Fourier transforms, definition 44Ч45
Fourier transforms, properties 45Ч47
Functions, named cosine integral 94
Functions, named error function 95
Functions, named exponential integral 95
Functions, named Fresnel cosine and sine integrals 95
Functions, named incomplete gamma function 95
| Functions, named sine integral 95
Gamma function, "derivation" 67Ч68
Gamma function, asymptotic expansion 70
Gamma function, definition 68
Gamma function, Euler expression 69
Gamma function, properties 84Ч85
Gamma function, Table,  70 70
Gamma function, Weierstrass formula 69
Green's functions, construction of 282Ч283
Green's functions, definition 281
Green's functions, solutions of differential equations 281 284Ч285 285 286
Harmonic balance, conservative oscillators 386Ч387
Harmonic balance, direct method 386Ч388
Harmonic balance, non-conservative oscillators 387Ч388
Harmonic balance, worked examples 389Ч394
Harmonic oscillator, 1-dim oscillator 336Ч337
Harmonic oscillator, 3-dim oscillator 339Ч342
Harmonic oscillator, matrix elements 338
Homoclinic orbit 166
Hopf-bifurcation theorem 186
Index, fixed-point 186
Integrals, evaluation of by parameter differential 104Ч108
Korteweg Ч de Vries equation 455Ч457
Krylov and Bogoliubov, first approximation 369
l'Hopital's rule 487
Laplace transfer, definition 53
Laplace transfer, properties 54Ч56
Laplace transfer, theorem 53
Laplace's equation, spherical coordinates 331Ч333
Leibnitz's relation 487
Level curve 178
Limit-cycle 151
Lindstedt Ч Poincare method, formal procedure 379Ч381
Lindstedt Ч Poincare method, Logistic equation 125Ч126 249Ч250
Lindstedt Ч Poincare method, secular terms 376Ч378
Lindstedt Ч Poincare method, worked examples 382Ч385
Linearly independent functions 221Ч222
Lotka Ч Volterra equations 173Ч177 179Ч180
mathematical equations 3Ч4
Mathematical equations, budworm dynamics 11Ч12
Mathematical equations, decay 6Ч7
Mathematical equations, Duffings 9Ч11
Mathematical equations, Fisher 8Ч9
Mathematical equations, logistic 7Ч8
Mathematical modeling 1Ч3
Node 118 122 135 143
Nonlinearity 12Ч13
Nullclines 133 138
Odd function 26Ч28
Orthogonal polynomials, general, differential equations 309
Orthogonal polynomials, general, generating functions 310Ч311
Orthogonal polynomials, general, interval of definition 309Ч310
Orthogonal polynomials, general, orthogonality relation 310
Orthogonal polynomials, general, recurrence relations 311
Orthogonal polynomials, general, Rodrique's relations 311
Orthogonal polynomials, general, weight functions 310
Orthogonal polynomials, general, zeros 312
Orthogonal polynomials, particular, functions, Chebyshev 315Ч317
Orthogonal polynomials, particular, functions, Hermite 314Ч315
Orthogonal polynomials, particular, functions, Laguerre 317Ч318
Orthogonal polynomials, particular, functions, Legendre 312Ч314
Orthogonal polynomials, particular, functions, Legendre, second kind and associated functions 319Ч321
Parseval's identity 33Ч34
Partial differential equations, general, linear 438Ч441 462Ч464
Partial differential equations, general, pulse solutions 443
Partial differential equations, general, similarity methods 459Ч464
Partial differential equations, general, soliton solutions 442
Partial differential equations, general, traveling waves 441 442
Partial differential equations, types of, advective 442Ч444 444Ч446
Partial differential equations, types of, Boltzmann problem 464Ч467
Partial differential equations, types of, Burgers' equation 444Ч446 461Ч462
Partial differential equations, types of, diffusion equations 462Ч464 467Ч469
Partial differential equations, types of, Fisher equation 448Ч455
Partial differential equations, types of, Korteweg Ч de Vries equation 455Ч457
Partial differential equations, types of, Schroedinger equation, nonlinear 457Ч459
Partial fractions 491Ч492
Periodic functions 25
Perturbation methods, general, general procedure 358 360Ч361
Perturbation methods, general, related issues 362
Perturbation methods, general, worked examples 362Ч367
Perturbation methods, particular techniques, averaging, first order 367Ч371 394Ч396
Perturbation methods, particular techniques, harmonic balance 385Ч388
Perturbation methods, particular techniques, Lindstedt Ч Poincare method 376Ч382
Phase space, one-dimension 118
Phase space, two-dimension 134Ч137 138Ч139
Physical equations 3Ч4
Piecewise continuous functions 31
Piecewise smooth function 31
Pulse solutions, PDE's 442
Riccati equation 239Ч241
Riemann Ц Lebesgue theorem 40
Routh Ч Hurwitz theorem 486
Saddlepoint 118 122 135 143
Schroedinger equation, nonlinear 457Ч459
Separation of variables, application 308
Separation of variables, constants of separation 309
Sign function 92
Similarity methods, applied to first-order PDE's 459
Similarity methods, applied to second-order PDE's 460
Similarity methods, invariance under stretching transformations 460
Similarity methods, stretching transformations 459
Similarity methods, worked examples 461Ч464
Since integral 421Ч423
Soliton solution 442
Special functions 273Ч275
Special functions, associated Laguerre 274
Special functions, associated Legendre 274
Special functions, Chebyshev 246Ч248 274
Special functions, Hermite 274
Special functions, Laguerre 274
Sphere, in uniform flow 334Ч335
Square wave 35Ч36 56Ч57
Stability, asymptotically stable 141
Stability, linear 122Ч124 139Ч140
Stirling numbers 213
Stirling's formula 70 419
Stretching transformations 459Ч460
Sturm Ч Liouville problems, comparison theorem 266
Sturm Ч Liouville problems, definition 270
Sturm Ч Liouville problems, eigenfunctions and eigenvalues 270
Sturm Ч Liouville problems, orthogonality of eigenfunctions 271Ч272
Sturm Ч Liouville problems, separation theorem 266
Symmetries 134 163
Theta function 91
traveling wave 441
Traveling wavefront 442
van der Pol equation 374Ч376 383Ч385 393Ч394 398Ч399
Vibrating string, boundary conditions 260
Vibrating string, differential equation 260
Vibrating string, fixed and free ends 262Ч263
Vibrating string, fixed ends 260Ч261
Vibrating string, free ends 263Ч264
Watson's lemma 417
Wave equations, linear 51Ч52 438Ч441
Wave equations, linear, d'Alembert solution 441
Weight function 272
Zeta function, Riemann, definition 72
Zeta function, Riemann, generalized 74Ч75
Zeta function, Riemann, prime numbers 75Ч76
Zeta function, Riemann, properties 73
Zeta function, Riemann, related functions 73Ч74
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



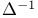
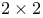 matrix
matrix 