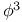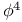|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Amit D.J. — Field theory, the renormalization group, and critical phenomena |
|
|
 |
| Предметный указатель |
Self-energy 85—86 121 123
Sengers, J.V. 309
Series, high temperature 237
Shirkov, D.V. xv
Shrock, R.E. 381
Simon, B. 32 36
Sink of bacteria 199
Soft insertion 373
Source 16—17 22 26—27 29 38—45 91—92 95 134 167—169
Source of bacteria 199
Space-like momenta 67
Specific heat 5 20 28—29 31 108 143 210—212 294 321 343
Specific heat, amplitude of 290 306
Specific heat, discontinuity 109
Spherical model 6 104 127 146
Spin space 8—9 30
Spin — 1/2 fermions 67 185
Spin: continuous 21—26 31
Spin: discrete 14
Spin: fixed magnitude 365
Spinors 67
Spontaneous magnetization see “Symmetry broken”
Stability, boundary of 334 335
Stability, domain of see “Fixed point”
Stability, of energy 331 333 334 335
Stability, wedge 332 338
Stanley, E.H. 146
Star of k 14
State: broken symmetry see “State ordered”
State: IN 48
State: ordered 84 96 107—108 112 134—136 166 354
State: OUT 48
State: zero temperature 365
Statistical weight 11 17 40
Stauffer, D. 322
Steepest descent 137—142
Stora, R. 79
Stratonovich, D.A. 32
Stueckelberg, E.C.G. 227
Summit 328
Super-renormalizable theory 154
Super-solid 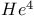 339 339
Super-symmetry 339
Superconductor 8 14 324 329
Supercooling 94
Superfluid 4 8 15 339
Superfluid density exponent 4
Superfluid helium 3 4
Superheating 94
susceptibility 4 19—20 27 84 110—112 131 208 241—243 278 319
Susceptibility exponent see “Exponent”
Susceptibility longitudinal (easy) 136 347 353 355
Suzuky, M. 308
Symanzik theorem 309
Symanzik, K. 42 53 79 102 169 188 227 309
Symmetric: phase see “Symmetric state”
Symmetric: state 85 94—96 105 108—109 113—115 117 166 169 182 278 293 324 374
Symmetric: theory 92 164 205 238
Symmetry: breaking 324 333 337 338 339
Symmetry: breaking induced by fluctuations 337
Symmetry: breaking, quadratic 179 183 346—350
Symmetry: broken 9 17 19 82 84—85 87 103 106—107 134—137 142 143 166 174—178 182—183 324 334 367 369
Symmetry: continuous global 94 126 274 365
Symmetry: cubic 13 66 187 238 325 328
Symmetry: discrete 365
Symmetry: generic 323
Symmetry: internal 8 12 17 30 31
Symmetry: O(M) 65—66 78 79 104—105 126—237 171—174 179 182—183 187 217 325 328 347—351 354 367
Symmetry: point (SP), of momenta 160—161 172—173 186 191 252 259—262 288
Symmetry: restoration, by fluctuations 323 365
Symmetry: restoration, dynamic 274 323 367
Tadpole 132 145
Takahashi, Y. 87 102
Tarko, H.B. 322
Teller, E. 32
Temperature: condition 336
Temperature: dependence 1 11 135 206—207 241
Temperature: difference 111 275 313 335 343
Temperature: difference, expansion in 30 73 100 164
Temperature: difference, renormalized 165 182 333 335
Temperature: dimensionless 367
| Temperature: flowing 224 242 355—356 375
Temperature: high 374
Temperature: measure 15 25 113
Temperature: non-zero 374
Temperature: scaling 366
Temperature: zero 374—375
Tetra-critical point 339
Theory: 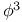 59 62 77 81 101 121 127 143 144 151 154—156 196 262 266 268 288 307 59 62 77 81 101 121 127 143 144 151 154—156 196 262 266 268 288 307
Theory: 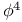 278 279 300 302 366 375 278 279 300 302 366 375
Theory:  154 186 154 186
Theory: classical 103 105—109
Theory: free (Gaussian) 24 26—28 31 34 42 45 156 162 185 238 243
Theory: M-vector see “Field multi-component”
Theory: massive 159—161 226
Theory: massless see “Critical theory”
Theory: O(M)-symmetric see “Symmetry”
Thermal wavelength 15
Thermodynamic limit 279
Thompson, C.J. 146
Thouless, D.J. 377 381
Time ordered products 37—38 43—45
Time ordering operator 37—38 42—45
Time, imaginary 40
Topological excitations 377
Toulouse, G xv 79
Transformation (Gaussian) to continuous fields 14—15 22—26 30—31
Transformation function, Schwinger 34—36 38
Transition see “Critical temperature”
Transition temperature, mean field 15 23 106 110
Transition, discontinuous 14—15
Transition, temperature free 26—28 106
Tri-critical point 170 243 335
Trimper, s. 341
Ultraviolet divergences see “Divergences”
Ultraviolet stability see “Fixed point”
Universal function 280 361
Universal quantities 226 246 274
Universal ratios of amplitudes 316—320 321
Universality 8 14 189 208 214 217 220 238—239 246 274 311—314 361
VACUUM 94
Vacuum part see “Graph”
Van Leeuwen, J.M.M. 239 269
Vector potential 14 182
Velocity function,  99 99
Velocity, fluid 199
Veltman, M. xv 52 148 155 161 188 227 250 269
Vertex 2 point 88—90 105 113 121 369
Vertex 3 point 108 262
Vertex function: dimension of 149 282 307
Vertex function: N-point 89 91 279
Vertex function: renormalized 123—124 157 161 172 191 198 219 286—288 292
Vertex function: with insertions 96—101 282—283 286—288
Vohrer, M. 269
Vortices 377
Wagner, H. 10 32 102 365
Wallace, D.J. 32 79 146 188 214 269 309 341 381
Ward — Takahashi identity 94—96 102 142 174—178 378
Ward, J.C. 87 102
Wave-vector 343
Wegner, F. xv 277 308
Weinberg theorem 213—214 226
Weinberg, E. 32 102 145 228 269 341
Weinberg, S. 164 188 227
Weiss theory 6
Wick rotation 34 40
Wick theorem 55—56
Widom, B. 5 6 9
Wiegmann, P.B. 381
Wilson function, calculation of 230—236
Wilson functions 192—194 198 213 215 218 240 243 245—246 248 256 267—268 348 357—358 192—194 198 213 215 218 240 243 245—246 248 256 267—268 348 357—358
Wilson, K.G. xv 54 79 145 188 190 204 214 221 227 239 269 295 309
Wilzeck, F. 227
Wortis, M. 322
Yaglom, A.M. 32
Yamagishi, H. 337 341
Yang, C.N. 52
Zanetti, M. 146
Zeros of 0 198
Zia, R.K.P. 32 79 188 309 381
Zimmerman, W. xv 52 188 296 309
Zinn-Justin, J. 54 79 102 146 165 169 188 190 227 269 308 309 322 365 369 378 381
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте