|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Diestel R. — Graph Theory |
|
|
 |
| Предметный указатель |
Ramsey graph 197
Ramsey numbers 191 193—194 209 210 232
Ramsey theory 189—208
Ramsey theory and connectivity 207—208
Ramsey theory, induced 196—206
Ramsey theory, infinite 192 208 210
Ramsey, F.P 190—193
Ramsey-minimal 196
Random graph 179 194 229—250 231
Random graph, evolution 241
Random graph, infinite 248
Random graph, process 250
Random graph, uniform model 250
Random variable 233
Random variable, indicator r.v. 234 295
Reducible configuration 121
Reed, B.A. 281
Refining a partition 1 155—159
Region 68—70
Region on 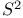 70 70
Regular 5 33 226
Regularity graph 161
Regularity graph, inflated, 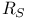 194 194
Regularity lemma 148 153—164 154 167 210
Renyi, A. 243 249
Richardson, M. 119
Rigid-circuit see “Chordal”
Riha, S. 228
Robertson, N. 66 121 183 186 257 264 275 281
Rodl, V. 167 194 197 211
Ronyai, L. 167
Root 13
Rooted tree 13 253 278
Rothschild, B.L. 210
Royle, G.F. 28
Rucihski, A. 249
Sanders, D.P. 121
Sarkozy, G.N. 226
Saturated see “Edge-maximal”
Schelp, R.H. 210
Schoenflies, A.M. 70
Schrijver, A. 145
Schur, I. 209
Scott, A.D. 167 178 209
Second moment 242—247
Self-minor conjecture 280
Separate a graph 10 50 55 56
Separate the plane 68
Separating set 10
Sequential colouring see “Greedy algorithm”
Series-parallel 185
Set system see “Hypergraph”
Seymour, P.D. 66 92 121 141 183 186 187 226 257 258 264 275 280 281
Shift-graph 209
Simonovits, M. 166 167 210
Simple basis 85 92—93
Simple graph 26
Simplicial tree-decomposition 261 275 279 281
Sink 125
Six-flow theorem 141
Snark 141
Snark planar 141 145 215
Sos, V. 152 166 167
Source 125
Spanned subgraph 3
Spanning subgraph 3
Spanning trees 13 14
Spanning trees, edge disjoint 58—60
Spanning trees, number of 248
Sparse graphs 147 169—185 194
Spencer, J.H. 210 249
Sperner’s lemma 41
Square of graph 218
Square, Latin 119
Stability number see “Independence number”
Stable set 3
Standard basis 20
Star 15 166 196
Star, induced 207
Star-shape 287
Steger, A. 117 122
Steinitz, E. 92
Stereographic projection 69
Stone, A.H. 151 160
Straight line segment 68
Strong core 289
Subcontraction see “Minor”
Subdividing vertex 18
Subdivision 18
Subgraph 3
Subgraph of all large k-connected graphs 207—208
Subgraph of high connectivity 11
Subgraph of large minimum degree 5—6 99 118
Subgraph, forced by edge density 147—164
Subgraph, induced 3
Sum of edge sets 20
Sum of flows 133
Supergraph 3
Symmetric difference 20 29—30 40 53
System of distinct representatives 41
Szabo, T. 167
Szekeres, G. 208 209
Szemeredi, E. 154 170 186 194 226
tail see “Initial vertex”
Tait, P.G. 121 227—228
Tangle 281
Tarsi, M. 121
ter(e) 23
Terminal vertex 25
Thomas, R. 121 183 208 210 258 280
Thomason, A.G. 66 170 179 186 241
| Thomassen, C. 65 92 106 121 179 185 187 228 281 282
Three colour theorem 97
Three-flow conjecture 141
Threshold function 241—247 250
Toft, B. 120 146
Topological isomorphism 76 78 88
Topological minor 17—18
Topological minor 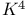 182 185 263 182 185 263
Topological minor 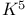 92 184 92 184
Topological minor 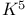 and and 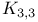 75 80—84 75 80—84
Topological minor  185 185
Topological minor 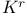 61 170—178 61 170—178
Topological minor 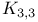 92 185 92 185
Topological minor and planarity 75 80—84 90
Topological minor and WQO of general graphs 278
Topological minor and WQO of trees 253
Topological minor as order relation 18
Topological minor of all large 2-connected graphs 207
Topological minor vs. ordinary minor 18—19 80
Topological minor, forced by average degree 61 170—178
Topological minor, forced by chromatic number 181
Topological minor, forced by girth 178
Topological minor, induced 178
Topological minor, tree (induced) 178
Torso 279
Total chromatic number 119
Total colouring 119
Total colouring, conjecture 119 122
Total value of a flow 126
Touching sets 258
Tournament 227
Transitive graph 41
Travelling salesman problem 227
TREE 12—14
Tree as forced substructure 13 178 185
Tree, cover 61
Tree, normal 13—14 27 139 144 296
Tree, threshold function for 247
Tree, well-quasi-ordering of trees 253—254
Tree-decomposition 186 255—262 278 280—281
Tree-decomposition, induced on minors 256
Tree-decomposition, induced on subgraphs 256
Tree-decomposition, lean 261
Tree-decomposition, obstructions 258—260 264—265 280 281
Tree-decomposition, part of 255
Tree-decomposition, simplicial 261 275 279 281
Tree-decomposition, width of 257
Tree-order 13
Tree-width 257—274
Tree-width and brambles 258—260 278 281
Tree-width and forbidden minors 263—274
Tree-width of a minor 257
Tree-width of a subdivision 278
Tree-width of grid 260 278 281
Tree-width, duality theorem 255—260
Tree-width, obstructions to small 258—260 264—265 280 281
triangle 3
Triangulated see “Cordal”
Triangulation see “Plane triangulation”
Trivial graph 2
Trotter, W.T. 194
Turan, graph 149—152 166 292
Turan, P. 150
Turan, theorem 150 195
Tutte polynomial 146
Tutte, flow conjectures 140—141
Tutte, W.T. 35 46 47 58 65 66 86 92 128 131 139 145 146 215 228
tw(G) 255
TX 16
Tychonov, A.N. 210
Unbalanced subgraph 247 249
Uniformity lemma see “Regularity lemma”
union 3
Unmatched 29
Upper density 166
Urquhart, A. 121
V(G) 2
Valency (degree) 5
Value of a flow 126
Variance 242
Vertex 2
Vertex cut see “Separating set”
Vertex of a plane graph 70
Vertex space 20
Vertex, colouring 95 98—103
Vertex, cover 30
Vertex-chromatic number 95
Vertex-connectivity 10
Vertex-transitive 41
Vince, A. 249
Vizing, V.G. 103 121 122 289 290 293
Voigt, M. 121
Wagner graph 183 261—262 279
Wagner, K. 84 93 183 184 185 186 281
Walk 9
Walk, alternating 52
Walk, closed 9
Walk, length 9
Well-ordering 294
Well-quasi-ordering 251—282
Welsh, D.J.A. 146
Wheel 46
Wheel theorem 46 65
Whitney, H. 66 80 89
Width of tree-decomposition 257
Winkler, P. 249
xP, Px, xPy, xPyQz, ... 7
xTy, ... 13
xy, 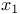 ... ...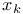 , ... 2 7 , ... 2 7
Zykov, A.A. 166
\ 70
‘Wagner’s Conjecture’ 281
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



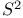
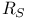

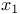 ...
...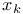 , ...
, ...