Авторизация
Поиск по указателям
Kincaid D., Cheney W. — Numerical analysis: mathematics of scientific computing
Обсудите книгу на научном форуме Нашли опечатку?
Название: Numerical analysis: mathematics of scientific computingАвторы: Kincaid D., Cheney W. Аннотация: This book has evolved over many years from lecture notes that accompany cer-
Язык: Рубрика: Математика /Численные методы /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1991Количество страниц: 690Добавлена в каталог: 15.07.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Implicit numerical methods 618 Inconsistent 591 637 650 Inconsistent systems 262 591 645 Infimum, inf 14 Injective 26 Inner product 191 204 227 411 412 596 Inner-product space 245 360 Integer representation 30 Integral equation 498 Integral of 339 Integration via polynomial interpolation 444 Intermediate — Value Theorem for Continuous Functions 13 57 Interpolate 278 Interpolating function, smoothest possible 321 Interpolation by multiquadrics 400 Interpolation in higher dimensions 385 Interpolation matrix 345 Interpolation phase 624 Interpolation polynomials in Newton’s form 279 Interpolation problem 385 Inverse 119 Inverse function 541 Inverse power method 232 Invertible 119 Involution 256 Iterated contraction 88 Iteration matrices, Gauss — Seidel 194 203 Iteration matrices, Jacobi 193 203 Iteration matrices, Richardson 193 203 Iteration matrices, SOR 194 203 Iteration matrices, SSOR 194 203 Iterative improvement (refinement) 174 Iterative methods 181 Jacobi iteration (method) 182 185 196 Jacobian matrix 70 544 570 Jordan blocks 559 Jordan canonical form 559 Julia set 105 Karmarker algorithm 113 661 Kepler’s equation 57 86 Knot array 425 Knot array, 511 Kolmogorov’s characterization theorem 372 Lagrange interpolating polynomials 282 Lagrange interpolation 281 305 435 Lagrange interpolation formula 282 309 Lagrange polynomial 283 Laguerre iteration 100 Laguerre iteration, algorithm 102 Laplace 607 Lax — Wendroff method 616 Least upper bound, lub 14 Least-squares problem 250 Least-squares theory 359 Legendre polynomials 366 Leibniz formula 304 Level-lines 207 LIMIT 1 Linear convergence 12 Linear dependence 642 Linear difference operator 21 Linear differential equations 555 Linear functional 477 512 642 Linear inequalities 636 642 643 Linear multi-step method 511 Linear programming 113 636 647 Linear systems 116 Linearizing 65 Linearly independent on a set 339 Lipschitz condition 488 Little 10 12 Local errors 516 Local multivariate interpolation method 396 Local roundoff error 494 Local truncation error 494 502 519 Localizing eigenvalues 240 Long calculations analyzed 36 Long operations 151 Loss of significance 41 Lower bounds 14 Lower-triangular structure 126 Lower-triangular structure, 129 Machine epsilon 35 Machine number 30 Machine precision 35 36 Maclaurin series 354 406 Magnitude 191 Mantissa 29 MARC-32 29 Marsden’s identity 341 Mathematical software libraries 78 Matrix condition number 166 Matrix exponential 557 564 Matrix method 578 Matrix norms 163 Matrix properties 119 Maximum deviation points 425 Mean — Value Theorem 3 Mean — Value Theorem for Integrals 12 Method of interval halving 58 Method of undetermined coefficients 446 510 Midpoint rule 454 Milne method 519 Minimal solution 262 267 Model problem 552 632 Modified Euler’s method 500 506 567 Modified Gram — Schmidt algorithm 248 Modulus 226 Modulus of continuity 350 Monic polynomial 286 451 459 Monomial matrix 124 Moving least squares 399 Multi-index 401 Multi-step methods 508 516 Multi-step methods, 403 Multigrid method 622 multinomial 401 Multiple shooting 544 Multiple zeros 24 Multiplicity of a zero 89 Multipliers 139 148 Multiquadrics 400 NaN 32 Natural cubic spline 319 Natural ordering 587 Natural splines, theory of higher-degree 324 Nearby machine numbers 31 Nested multiplication 14 91 280 Neumann series 172 Neville’s algorithm 305 Newton divided-difference method 308 Newton form interpolation polynomial 279 Newton — Cotes formula 444 Newton — Raphson iteration 64 Newtonian scheme 393 Newton’s interpolation formula 312 Newton’s iteration for polynomials 94 Newton’s method 64 105 112 393 543 Newton’s method, algorithm 64 297 301 Nilpotent 560 Node set geometry 390 Nodes, choosing 287 Nondegeneracy assumption 654 Nonhomogeneous Farkas’ Theorem 644 Nonhomogeneous problem 562 Noninterpolatory approximation methods 349 Nonlinear equations 70 570 Nonnegative definite 138 Nonsingular 119 Normal equation 251 362 368 399 596 Normal matrix 242 Normalized floating-point 30 Normalized scientific notation 29 Normed linear space 171 Norms 161 NULL-SPACE 22 Numerical differentiation 430 431 Numerical instability 48 50 Numerical integration via interpolation 443 Numerical solution of ordinary differential, equations 486 Nyquist frequency 421 o-notation 10 12 Objective function 113 648 652 Operation counts, ops 151 630 Optimal feasible point solution 648 Optimization 648 Order of the multi-step method 513 Orders of convergence 85 Orders of convergence, linear 12 Orders of convergence, order 12 Orders of convergence, quadratic 12 Orders of convergence, superlinear 12 Ordinate array 425 Origin shift 272 Orthogonal 206 245 363 Orthogonal factorizations 245 Orthogonal polynomials 459 Orthogonal systems 365 Orthogonality condition 596 Orthonormal 245 363 Orthonormal base 365 Orthonormal system 363 Overflow 32 Parabolic equation 572 580 607 Parseval identity 369 Partial differential equations 572 Partitioned matrices 122 Peano kernel 477 Peano’s theorem 478 Penrose properties 264 Perfidious polynomial 55 Permutation 159 301 Permutation matrix 147 Permutation vector 128 Pivot element 139 Pivot row 140 145 146 Pivoting 143 Point evaluations 477 Point of attraction 105 Poisson’s equation 594 Polynomial interpolation 278 288 Positive definite 121 192 Power method 229 Power series 354 Precondition 213 Preconditioned conjugate gradient 213 Preconditioned conjugate gradient, algorithm 216 217 Predictor-corrector method 511 Principal minor 132 Problems without time dependence 586 591 Product 387 Product 13 Properties of B-splines 335 Pseudo inner-product 411 412 Pseudo-norm 411 412 Pseudocode, 130 Pseudocode, adaptive approximation 426 Pseudocode, adaptive quadrature 475 Pseudocode, back substitution 127 Pseudocode, back substitution on permuted system 128 Pseudocode, Bairstow’s algorithm 98 Pseudocode, basic Gaussian elimination 143 Pseudocode, basic Gaussian elimination, permuted system 145 Pseudocode, bisection algorithm 59 Pseudocode, boundary value problems, explicit method 576 Pseudocode, boundary value problems, implicit method 582 Pseudocode, boundary value problems, method of characteristics 613 Pseudocode, Chebyshev acceleration 201 Pseudocode, Cholesky factorization 134 Pseudocode, conjugate gradient iteration 210 211 Pseudocode, derivative approximation, central difference 434 Pseudocode, derivative approximation, forward difference 432 Pseudocode, derivative approximation, Richardson extrapolation 437 Pseudocode, divided differences 281 300 308 Pseudocode, Doolittle factorization 131 Pseudocode, extrapolation 201 Pseudocode, fast Fourier transform 419 Pseudocode, forward substitution 127 Pseudocode, forward substitution on permuted system 128 Pseudocode, Gauss — Seidel iteration 190 Pseudocode, Gaussian elimination, scaled row pivoting (factorization phase) 148 Pseudocode, Gaussian elimination, scaled row pivoting (solution phase) 148 Pseudocode, Gaussian quadrature 5— Pseudocode, Gaussian quadrature, point 459 Pseudocode, Gram — Schmidt algorithm 247 Pseudocode, Gram — Schmidt algorithm, modified 248 249 Pseudocode, Horner’s algorithm 92 280 Pseudocode, Horner’s algorithm, complete 93 Pseudocode, iterative method, scaling 186 Pseudocode, Jacobi iteration 186 Pseudocode, Laguerre’s algorithm 102 Pseudocode, multigrid damping errors example 625 Pseudocode, multigrid example 624 Pseudocode, multigrid V-cycle 630 Pseudocode, nested multiplication 14 Pseudocode, Newton’s algorithm 64 Pseudocode, Newton’s algorithm, implicit function 69 Pseudocode, Newton’s method, polynomial 94 Pseudocode, power method 230 Pseudocode, preconditioned conjugate gradient 216 217 Pseudocode, Richardson extrapolation 436 Pseudocode, Richardson iteration 184 Pseudocode, Romberg extrapolation 465 Pseudocode, Runge — Kutta method 499 Pseudocode, Runge — Kutta — Fehlberg method 505 Pseudocode, secant algorithm 76 Pseudocode, shifted 273 Pseudocode, solving 150 Pseudocode, solving 151 Pseudocode, solving tridiagonal system 155 Pseudocode, steepest descent 207 Pseudocode, Taylor-series method 491 Pseudocode, Taylor-series method for systems 527 Pseudoinverse 261 264 Pythagorean rule 246 361 Pythagorean rule, 251 269 Pythagorean rule, algorithm of Francis 269 Quadratic convergence 12 67 Quadratic form 122 Quadrature formulas 456 Quasi-interpolation operators 349 Quasi-linear second-order equations 606 Radius of convergence 355 Range reduction 45 Ratio Test 355 356 Rayleigh — Ritz method 595 Recurrence relation 22 49 Recursive formulas for continued fractions 404 Recursive trapezoid rule 466 Reduction to upper Hessenberg form 270 Reflections 251 Region of absolute stability 570 Relative error 41 Relative error analysis 36 Remainder 2 Remainder theorem 89 Remez first algorithm 381 Residual vector 166 174 554 Restriction 339 627 Restriction of 339
Реклама
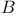-splines 
-step multi-step method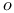 
, functions and sequences 
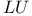-decomposition (factorization) 
-th convergence 
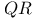-algorithm 
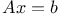given 
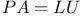
given 
to 
|
|
О проекте