|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Arcangeli R. — Multidimensional Minimizing Splines |
|
|
 |
| Предметный указатель |
 -spline, basis -spline, basis  -splines 64 -splines 64
 -spline, over -spline, over  ix 3 ix 3
 -spline, over -spline, over  136—140 136—140
 -spline, over -spline, over  ix 59 “Smoothing over ix 59 “Smoothing over
 -spline, over -spline, over  , regularity 65 , regularity 65
 -spline, space of s over O 64 -spline, space of s over O 64
 -spline, univariate -spline, univariate  -spline see “Univariate -spline see “Univariate  -spline” -spline”
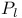 -unisolvent set xv -unisolvent set xv
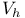 -discrete interpolating -discrete interpolating  -spline see “Discrete interpolating -spline see “Discrete interpolating  -spline” -spline”
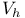 -discrete smoothing -discrete smoothing  -spline see “Discrete smoothing -spline see “Discrete smoothing  -spline” -spline”
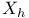 -discrete smoothing -discrete smoothing  -spline see “Discrete smoothing -spline see “Discrete smoothing  -spline” -spline”
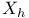 -discrete smoothing -discrete smoothing  -spline with tangent conditions 225 -spline with tangent conditions 225
(m,l,s)-spline see “Interpolating” and “Smoothing (m
(m,s)-spline ix 3
(m,s)-spline, explicit expression 17
(m,s)-spline, regularity 20
(m,s)-spline, space of (m,s)-splines 15
Adams, R.A. xiv 50 136 201
Akima, H. 132
Allasia, G. 132 160
Andor, L. 227
Apprato, D. 61 80 87 100 105 107 175 199 222
Approximation error of discrete, interpolating  -splines 80 -splines 80
Approximation error of discrete, smoothing  -splines 87 -splines 87
Approximation error of interpolating,  -splines over -splines over  68 68
Approximation error of interpolating, (m,l,s)-splines 55
Approximation error of interpolating, (m,s)-splines 37
Approximation error of smoothing,  -splines over -splines over  68 68
Approximation error of smoothing, (m,l,s)-splines 56
Approximation error of smoothing, (m,s)-splines 49
Approximation operator 70
Arcangeli, R. 32 33 45 47—49 52 61 75 87 105 107 131 132 147 175 199 222
Arge, E. 132
Argyris triangle 71 108
Argyris triangle, of class 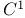 107 109 107 109
Argyris triangle, of class 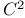 107—110 107—110
Aronszajn, N. 3
Arsenine, V. 81
Atteia, M. ix 3 59
B-spline ix 98
Banach — Steinhaus theorem 34
Banach's isomorphism theorem 9 11
Basis  -splines 64 -splines 64
Basis of normalized cubic B-splines 98
Bell triangle 71 108
Bell triangle, of class 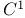 107—109 107—109
Bell triangle, of class 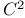 107—110 107—110
Benbourhim, M.N. 24
Bernardi, C. 145
Besenghi, R. 132 160
Bezier surface ix
Bogner — Fox — Schmit rectangle 71 108
Bogner — Fox — Schmit rectangle of class 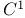 88 88
Bogner — Fox — Schmit rectangle, of class 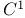 107 109 107 109
Bogner — Fox — Schmit rectangle, of class 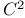 107 109 107 109
Bogner — Fox — Schmit rectangle, of class 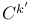 108 108
Bouhamidi, A. 53-55
Bramble — Hilbert lemma 201
Brezis, H. xiv 9-11 34 112
Ciarlet, P.G. x xv 33 40 66 69—71 87 107 112 132 145 181 201 203
Clamped cubic spline 97
Clement's, operator 75 225
Clement's, result 70 71 107 145 146 149 179 225
Clement, P. 70 71 76
Closed graph theorem 10
Convergence of discrete, interpolating  -splines 77 -splines 77
Convergence of discrete, smoothing  -splines 84 147 152 182 184 204 205 226 -splines 84 147 152 182 184 204 205 226
Convergence of interpolating,  -splines over ft 67 -splines over ft 67
Convergence of interpolating, (m,l,s)-splines 55
Convergence of interpolating, (m,s)-splines 29
Convergence of smoothing,  -splines over ft 66 67 -splines over ft 66 67
Convergence of smoothing, (m,l,s)-splines 56
Convergence of smoothing, (m,s)-splines 40 42
Convergence of smoothing, (m,s)-splines for noisy data 50 52
Craven, P. x 41 81
Crease 131
Dahmen, W. ix
Data, hard data 110
Data, Hermite data 111 131 140 147 148
Data, Lagrange data 73 110 114 131 140 147 148 157
Data, of seismic origin 111
Data, orientation data 224
Data, position data 224
de Boor C. ix
de Rossi, A. 160
de Silanes, Lopez, M.C. 45 47–49 52 55 56 80 87 131 132 160
Deny, J. 6
DIP 111 131 224
Discontinuity, detection 160 163
Discontinuity, set 131-133 148 160
Discrete  -spline ix 59 69 -spline ix 59 69
Discrete interpolating  -spline, approximation error 80 -spline, approximation error 80
Discrete interpolating  -spline, computation 73 143 -spline, computation 73 143
Discrete interpolating  -spline, convergence 77 -spline, convergence 77
Discrete interpolating  -spline, definition 72 142 -spline, definition 72 142
Discrete interpolating  -spline, variational characterization 72 142 -spline, variational characterization 72 142
Discrete smoothing  -spline, approximation error 87 -spline, approximation error 87
Discrete smoothing  -spline, computation 81 107 144 181 223 -spline, computation 81 107 144 181 223
Discrete smoothing  -spline, convergence 84 147 152 182 184 204 205 226 -spline, convergence 84 147 152 182 184 204 205 226
Discrete smoothing  -spline, definition 80 143 152 181 203 223 -spline, definition 80 143 152 181 203 223
Discrete smoothing  -spline, variational characterization 80 143 180 202 223 -spline, variational characterization 80 143 180 202 223
Discrete space of  -splines 73 -splines 73
Disk-like surface 220
Duchon, J. ix 3 5—7 16 20 22 29 31 33 34 36 175
Dyn, N. ix 26
Extension theorem for Sobolev spaces xv
fault 131 133
Fault, detection see “Discontinuity detection”
Fault, line 144 157 160 162
Fault, oblique 131 144
Fault, vertical 131 144 157
Finite element framework 69
Floater, M.S. 132 221 234
Fourier transform xiii
Franke's function 113
Franke, R.F. 105 113 132
Friedrichs' theorem 8 24 65
Functional spaces,  xiv xiv
Functional spaces,  , norm on xiv , norm on xiv
Functional spaces,  134 134
Functional spaces,  , norm on 134 , norm on 134
Functional spaces,  219 219
Functional spaces,  , norm on 219 , norm on 219
Functional spaces,  135 135
Functional spaces,  , norm on 137 146 , norm on 137 146
Functional spaces,  xiii xiii
Functional spaces,  , norm on xiii 62 177 204 , norm on xiii 62 177 204
Functional spaces, 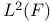 176 176
Functional spaces, 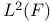 , norm on 176 , norm on 176
Functional spaces,  53 53
Functional spaces,  , norm on 54 , norm on 54
Functional spaces,  6 6
Functional spaces,  , norm on 8 10 11 28 , norm on 8 10 11 28
Functional spaces,  5 5
Functional spaces,  , norm on 5 , norm on 5
Functions of the Euclidean distance 16
Gaches, J. 61
GCV see “Generalized cross validation”
Generalized cross validation, function 81 182 224
Generalized cross validation, method x 41 81 114 161 162 182 189 224 229 235 236 241
Generalized maximum likehood 81
Geymonat, G. 32
Girard, D. 160
Goulaouic, C. xiv
Gout, C. 199
Gout, J.L. 75
Greiner, G. 221
Grisvard, P. xiv 31 176
Gu, C. x 41 81
Gutzmer, T. 160
| Hardy, R.L. 21
Hausdorff distance 3 27 67 184
Hollig, K. ix
Hormander, L. 13 62 65
Hormann, K. 221
Hoschek, J. 235
Hsieh — Clough — Tocher triangle of class 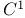 110 110
Hsieh — Clough — Tocher triangle of class 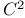 110 110
Hsieh — Clough — Tocher triangle, reduced of class 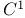 110 110
Hutchinson, M.F. 82
Hwang, W.L. 160
Index set, 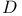 27 42 55 67 74 145 148 183 204 220 27 42 55 67 74 145 148 183 204 220
Index set, 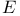 177 199 177 199
Index set, 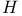 69 140 145 148 179 202 222 69 140 145 148 179 202 222
Index set, 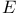 74 74
Influence matrix 81 182
Interpolating  -spline over -spline over  , approximation error 68 , approximation error 68
Interpolating  -spline over -spline over  , convergence 67 , convergence 67
Interpolating  -spline over -spline over  , definition 61 , definition 61
Interpolating  -spline over -spline over  , variational characterization 63 , variational characterization 63
Interpolating (m,l,s)-spline, approximation error 55
Interpolating (m,l,s)-spline, convergence 55
Interpolating (m,l,s)-spline, definition 54
Interpolating (m,l,s)-spline, explicit expression 54
Interpolating (m,s)-spline, approximation error 37
Interpolating (m,s)-spline, computation 25
Interpolating (m,s)-spline, convergence 29
Interpolating (m,s)-spline, definition 13
Interpolating (m,s)-spline, variational characterization 14
Interpolation-smoothing mixed method 110
Inverse assumption 87
Iske, A. 160
Klein, P. 132
Kruth, J.P. 220
Laghchim-Lahlou, M. 110
Lagrange multiplier 14 63 73 112
Lasser, D. 235
Laurent, P.-J. 3 82 95 132 160
Lax — Milgram lemma 40 66 181 203
le Mehaute, A. 53—55 107 132
Lee, D. 160
Levin, D. 26
Lions, J.L. xiv 6 8 24 65
Lipschitz-continuous boundary xiv
Local sequential weak compactness theorem xv
Lodha, S.K. 105
Ma, W. 220
Magenes, E. xiv 8 24 65
Mallat, S. 160
Manzanilla, R. 105 107 131—133 147
Michelli, C.A. ix
Minimizing spline ix
Morrey, C.B. 75
Multiquadric function 21
Natural cubic spline 96
Natural polynomial spline 92
Necas, J. xiv 3 6 32 47 62 137 176 203 205
Nielson's function 113
Nielson, G.M. 113 132
Non-regular function 131 224
Normalized cubic B-splines 98
Normalized cubic B-splines, basis of 98
Paihua, L. 26
Parameter correction 227 235
Parametrization method 220
Parra, M.C 131 132 160
Pasadas, M. 131 132 225
Peetre, J. 5 185
Phillips, R. 132
Plancherel's Theorem 93
Polyharmonic spline ix 19
Powell — Sabin triangle 132
Powell — Sabin triangle, of class 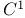 110 110
Powell — Sabin triangle, of class 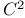 110 110
Powell, M.J.D. 110 132
Prenter, P.M. 99
Pseudo-cubic spline 21
Pseudo-quintic spline 21
Ragozin, D. 52
Raviart, P.-A. 71
Reference surface 221
Regularity, of  -splines over -splines over  65 65
Regularity, of (m,s)-splines 20
Regularized equation 81
Reimers, M. 221
Relative error 114 228
Rellich — Kondrasov compact imbedding theorem xiv
Renner, G. 227
Riemenschneider, S. ix
Rippa, S. 26
Rossini, M. 160
Rozhenko, A.I. 132
Sabin, M.A. 110 132
Sablonniere, P. 110
Sanchez, A.M. 32 33
Schumaker, L.L. ix 92 95 99
Schwartz, L. xiii 3 6 7 16 17 19
Scott, L.R. 70
Serres, C. 132
Shape-preserving parametrization method 234
Smoothing  -spline over -spline over  , approximation error 68 , approximation error 68
Smoothing  -spline over -spline over  , convergence 66 67 , convergence 66 67
Smoothing  -spline over -spline over  , definition 66 , definition 66
Smoothing  -spline over -spline over  , variational characterization 66 , variational characterization 66
Smoothing (m,l,s)-spline, approximation error 56
Smoothing (m,l,s)-spline, convergence 56
Smoothing (m,l,s)-spline, definition 55
Smoothing (m,s)-spline, approximation error 49
Smoothing (m,s)-spline, computation 40—41
Smoothing (m,s)-spline, convergence 40 42
Smoothing (m,s)-spline, convergence, for noisy data 50 52
Smoothing (m,s)-spline, definition 39
Smoothing (m,s)-spline, variational characterization 39
Sobolev's continuous imbedding theorem xv
Sobolev's Holder imbedding theorem xiv
Space, of  -splines over -splines over  92 92
Space, of  -splines over -splines over  64 89 92 64 89 92
Space, of (m,s)-splines 15
Space, of clamped cubic splines 97
Space, of discrete  -splines 73 -splines 73
Space, of natural cubic splines 96
Space, of natural polynomial splines 92
Splines defined by local mean values, computation 24
Splines defined by local mean values, definition 22
Springer, J. 132
Stampacchia's theorem 112
Strang, G. 32 70 71
Strike 111 131 224
Tarrou, C. 132 144
Theorem, Banach — Steinhaus 34
Theorem, Banach's isomorphism 9 11
Theorem, closed graph 10
Theorem, corollary of Urysohn's 13 62
Theorem, extension theorem for Sobolev spaces xv
Theorem, Friedrichs' 8 24 65
Theorem, local sequential weak compactness xv
Theorem, Plancherel's 93
Theorem, Rellich — Kondrasov compact imbedding xiv
Theorem, Sobolev's continuous imbedding xv
Theorem, Sobolev's Holder imbedding xiv
Theorem, Stampacchia's 112
Thin plate spline ix 20
Tikhonov, A. 81
Torrens, J.J. 107 131—133 147 160 222
Trapezoidal rule 179 188
Treves, F. xiii
Trial and error 41 81
Uniformity property 71
Univariate  -spline, explicit expression 89 -spline, explicit expression 89
Univariate  -spline, interpolating, computation 93 -spline, interpolating, computation 93
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -spline, basis
-spline, basis 


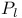 -unisolvent set
-unisolvent set 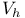 -discrete interpolating
-discrete interpolating 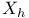 -discrete smoothing
-discrete smoothing