Пусть

– топологическое кольцо и
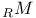
– некоторый левый унитарный
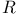
-модуль. Известно, что множество
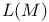
всех

-модульных топологий на
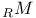
образует полную модулярную решетку. Топологию
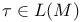
будем называть \textit{

-предмаксимальной}, если в
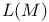
существует максимальная по включению цепь

такая, что
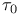
– наибольший элемент в
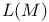
и

. В \S 1 получены условия, каждое из которых обеспечивает либо наличие, либо отсутствие 1-предмаксимальных хаусдорфовых топологий на
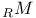
. \S 2 содержит описание всех

-предмаксимальных топологий в случае, когда

– топологическое тело, топология которого определяется вещественной абсолютной величиной.
 |
|
О проекте
|
|
О проекте


 – топологическое кольцо и
– топологическое кольцо и 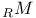 – некоторый левый унитарный
– некоторый левый унитарный 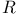 -модуль. Известно, что множество
-модуль. Известно, что множество 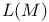 всех
всех 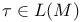 будем называть \textit{
будем называть \textit{ -предмаксимальной}, если в
-предмаксимальной}, если в  такая, что
такая, что 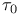 – наибольший элемент в
– наибольший элемент в  . В \S 1 получены условия, каждое из которых обеспечивает либо наличие, либо отсутствие 1-предмаксимальных хаусдорфовых топологий на
. В \S 1 получены условия, каждое из которых обеспечивает либо наличие, либо отсутствие 1-предмаксимальных хаусдорфовых топологий на 