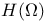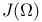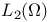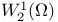Ladyzhenskaya O.A. — Mathematical theory of viscous incompressible flow :: Электронная библиотека попечительского совета мехмата МГУ

Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск Форум

Авторизация

Поиск по указателям

Ladyzhenskaya O.A. — Mathematical theory of viscous incompressible flow

Обсудите книгу на научном форуме

Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter

Название: Mathematical theory of viscous incompressible flow

Автор: Ladyzhenskaya O.A.

Аннотация:

In the three years since the Russian edition of this book was written, quite a few papers devoted to a mathematically rigorous analysis of nonstationary solutions of the Navier-Stokes equations have been published. These papers either pursue the investigation of differential properties of the solutions whose existence and uniqueness is proved in the present book, or else they give other methods for obtaining such solutions. However, the basic problem of the unique solvability "in the large" of the boundary-value problem for the general three-dimensional nonstationary Navier-Stokes equations (with no assumptions other than a certain smoothness of the initial field and of the external forces) remains as open as ever.

Язык:

Рубрика: Физика/Классическая физика/Механика жидкости и газа/

Статус предметного указателя: Готов указатель с номерами страниц

ed2k: ed2k stats

Издание: second revised edition

Год издания: 1969

Количество страниц: 224

Добавлена в каталог: 19.06.2005

Операции: Положить на полку | Скопировать ссылку для форума | Скопировать ID

Предметный указатель

Adhesion condition      34
Agmon, S.      219
Aronszajn, N.      215
Averaging kernal      15
Averaging operation (operator)      15 16 38 132 134
Averaging radias      132 159
Babich, V.M.      215
Banach — Steinhaus theorem      160 181
Berker, R.      220
Bernstein, S.N.      203 217
Birkhoff, G.      215
Brushlinskaya, N.N.      220
Bykovski, E.B.      203 204 217
Caccioppoli, R.      203 217
Calderon, A.P.      218
Chudov, L.A.      220
Complete system of functions in $J_{0, 1}(\Omega)$       156
Completely continuous operator      31
Couetteflow      2
Courant, R.      215 218
Crudeli, V.      204
Cutoff function(s)      41 120 124 204
Dirac delta function      35 50
Dirichlet problem      42
Douglis, A.      219
Eidel'man, S.A.      219
Elliptic operators      18 67 203 204
Energy conservation law      147
Equation of continuity      33
Euler — D'Alembert paradox      1
Faddeyev, M.D.      206
Finn, R.      43 113 114 213 214 216 218 219
Flow past objects, problem of      33 41 113 124—126
Fourier method      104
Fourier transform      50 108
Friedrich's lemma      176
Friedrichs, K.O.      203 204 207 215 217 220
Fujita, H.      213 215 219
Functions of compact support      8
Fundamental singular solution      42 49 65 138 205
Gagliardo, E.      203 219
Galerkin's method      34 81 156 175 181 206
Gelfand J.M.      216
Generalized derivative      7 22
Generalized functions      37 50
Generalized solution      15 34 42 115 120 142 143
Generalized solution of the problem of flow past objects      124
Generalized solution of the Stokes problem      35
Gevray, M.      219
Glazman, I.M.      216
Gol'dshtik, M.A.      3 217
Golovkin, K.K.      6 167 203 205 207 217 219 220
Greco, D.      218
Green's formula(s)      53 139
Guseva, O.V.      205 218
Gyunter, N.M.      57 185 207 215 218 219 220
Hilbert, D.      215 218
Hopf's (weak) solution      146 208 211 212
Hopf, E.      6 142 173 207 208 211 212 213 215 215
Ilin, V.P.      203
Imbedding theorems      8 11 13 108 159 203
Integrals of potential type      13 [203
Ito, S.      219
Kato, T.      217 219
Kellogg, O.D.      218
Kibel, I.A.      216
Kinematic viscosity      6 33
Kiselev, A.A.      6 82 216 220
Kochin, N.E.      216
Korn, A.      204
Koshelev, A.I.      218
Krasnoselski, M.A.      208 217
Krein, S.G.      203 204 208 217
Krylov, A.L.      220
Kuskova, G.V.      220
Kzhivitskii, A.      220
Ladyzhenskaya, O.A.      215 216 217 220
Laplace operator      5 42 47 66 120 203
Lax, P.      217
Leray — Schauder principle      31 117
Leray, J.      6 113 138 142 205 206 207 213 215 216 215
Lichtenstein, L.      49 113 204 206 218
Lin, C.C.      220

Linear functional      31
Lions, J.L.      208 212 215 220
Lorentz, A.A.      204
Lyapunov surface of index ft      23 52 57 66
Marcinkiewicz lemma      108
Marcinkiewicz, J.      108 216
Matrix Green's function      65
Maxwell — Boltzmann equations      6
Method of finite differences      81
Mikhlin, S.G.      108 216
Miranda, C.      215
Navier — Stokes equations      1
Navier — Stokes equations, general system of      141
Navier — Stokes equations, nonlinear      113
Navier — Stokes equations, nonstationary linearized      81
Neumann problem      24
Nikolski, S.M.      108 216
Nirenberg, L.      203 219
Noll, W.      216
Odqvist, F.K.      6 49 113 204 206 215
Ohyama, T.      211 215
Plemelj, J.      204
Poiseuille flows      2
Poisson's equation      21
Potential flows      1
Potential theory      205
Potential: biharmonic volume      22
Potential: electrostatic      49 64 67
Potential: hydrodynamical      47
Potential: Newtonian      12 21 22 136
Potential: nonstationary      6 191 205 207
Potential: of a double layer      49 53—58 60 63 69 71
Potential: of a single layer      49 53—58 60 63
Potential: volume      49—53 68 69
Prodi, G.      208 212 275 220
Rellich's theorem      12
Reynolds number      2—5 113 118 172 206
Reynolds number, critical value of      3
Reynolds number, generalized      118 141 171
Riesz' theorem      31 38 116
Roze, N.V.      216
Rusanov, B.V.      43 276
Scalar product      7 8 23 31 115
Schauder, J.      113 206 276
Schwartz, L.      276
Serrin, J.      211 279
Shilov, G.E.      276
Simuni, L.M.      220
Slobodetski, L.N.      275 276
Smirnov, N.V.      204 277
Smirnov, V.I.      275
Sobolev, S.L.      7 108 203 207 275 277
Sobolevski, P.E.      208 209 211 277 218
Solenoidal field      24 29 41
Solenoidal vectors      24 30
Solenoidal vectors, infinitely differentiable      27
Solonnikov, V.A.      6 78 100 167 205 207 212 277 275 279
Space: $G(\Omega)$       23 27
Space: 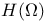$H(\Omega)$       31
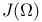Space: $J(\Omega)$       23 27 44 156
Space: $J_{0, 1}(\Omega)$       31 156
Space: 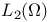$L_{2}(\Omega)$       8 23
Space: 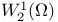$W_2^1(\Omega)$       8
Space: $W_2^l(\Omega)$       7
Space: $W_r^{l-1/r}(S)$       68
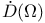Space: $\dot D(\Omega)$       17 18
Space: $\dot J(\Omega)$       27
Space: W      83
Star-shaped domains      30
Stokes paradox      43 103
Stokes problem      35 65 103 204
Stream function      42
Stress tensor      53 58 61
Theory of generalized solutions      207
Turbulent solutions      207
Vishik, M.I.      277
Vorovich, I.I.      206 213 27 218
Weak solution      4 5 142 146 174
Wiener, N.      207 220
Wieyl, H.      277
Wolibner, W.      185 279
Young's inequality      10
Yudovich, V.I.      206 211 213 277 218 219 220
Zygmund, A.      218

О проекте