|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Frisch U. — Turbulence. The legacy of A.N. Kolmogorov |
|
|
 |
| Предметный указатель |
 -model 135—140 -model 135—140
 -model, exact for Burgers' equation 143 -model, exact for Burgers' equation 143
 -model, history 180 181 -model, history 180 181
 -model, Novikov — Stewart formulation 167 -model, Novikov — Stewart formulation 167
 -model, random 167 -model, random 167
 see lognormal model see lognormal model
Absolute equilibrium 209 242
Active scalar 202
Alpha effect 232
Analyticity 126
Analyticity, strip 117
Anisotropic kinetic alpha (AKA) effect 232
Anomalous scaling for scalars 216—217
Anticommuting ghost fields 214
Arnold — Beltrami — Childress (ABC) flow 204
axial anomaly 77
Bifractal model 140—143
Bifractal model, Burgers' equation 142
Bifurcation, Andronov — Hopf 4 72
Bifurcation, symmetry-increasing 11
Blow-up 202 221
Blow-up for Euler (ideal) flow 115—119
Blow-up for viscous flow 119
Blow-up of supremum of vorticity 200 201
Blow-up, not implied by fractal / multifractal models 199
Blow-up, spurious, predicted by closure 221
Boltzmann equation 225
boundary conditions 1 2 6
Breakdown of hydrodynamics 110
Brownian motion 48 121 205
Burgers' equation 142 142; refined
Burgers' equation, blow-up at zero viscosity 199
Burgers' equation, failure of all-order perturbation theory 216
Burgers' vortex 187 252
Cahn — Hilliard equation 234
Cancellation index 191
Cantor set 122 130 137
Cascade 21; see also energy
Cascade in two dimensions 243
Cascade of enstrophy 242 251
Cascade of helicity 21
Cascade, deterministic model of 171
Cascade, inverse 251
Cascade, nonconservative 166
Cascade, random model of 165—168 170 171 173 179 180
Cascade, Richardson 100 103—106 135 179 235
Cascade, terminated almost surely 137; see also fractal dimension (negative)
Cascade, two-dimensional 241
Catastrophes, battle of 141
Central limit theorem 51
Chaos xi 8 31 38 72 116 204;
Chaotic advection 204
Characteristic function 41
Characteristic functional 46
Chiral nonlinearity 234
Circulation 18 191 191
Circulation time 71
Closure 98 197 206 211
Closure is renormalization group conceptually superior? 240
Closure, its shortcomings 219—221
Closure, law of decay of energy 115
Closure, Obukhov's derivation of 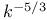 law 98 law 98
Closure, realizable 220
Codimension 130 136
Coherent structures 108 182 199 243 252
Composite operators 216
Compressible turbulence 197
Conservation laws 18—21
Cramer function 148 161 169 169 171—173
Cramer renormalization 182
Critical phenomena 235
Critical phenomena, dynamical 236
Cumulants 44 210
Cumulants, hierarchy 210 211 220
Cylinder 2
D(h) 144 148;
Debye screening 192
Decay see energy (law of decay of)
Decimation 238
Degrees of freedom 106—110 150 192 204 243
Degrees of freedom, microscopic / macroscopic 110
Degrees of freedom, predicted by K41 107 150
Depletion of nonlinearity 119 201 243 251 252
Depletion of nonlinearity, not captured by closure 221
Deterministic chaos 27—36 171
Devil's staircase 122
Diagrammatic methods 44 115 214—217
Diffusion, anomalous 231
Diffusion, equation 228 230
Diffusion, subdiffusive 231
Diffusion, superdiffusive 231
Diffusivity, effective 226
Dimension of attractor 108 204; two-dimensional
Direct interaction approximation (DIA) 105 197 206 217—219
Dissipation fluctuations see multifractal model refined
Dissipation range 92; see also intermittency K41 multifractal spectrum
Dissipation range, far 152
Dissipation rate see energy (dissipation rate)
Dissipation, correlation function 216
Dissipation, scale (Kolmogorov) 91
Dissipation, wavenumber 91
Dissipativity 200 243
Dominant balance 229
Drag coefficient 67
Drag crisis 69
Dynamical systems 36 37 73 108 126 180 181 203—205 205; fractals
Eddy damped quasi-normal Markovian approximation (EDQNM) 206 220
Eddy diffusivity 222 226—228 230 231
Eddy diffusivity, Taylor's expression 231
Eddy noise 238 239
Eddy turnover time 101
Eddy turnover time, large 106
Eddy viscosity xii 105 233
Eddy viscosity, caveats 233
Eddy viscosity, complex 233
Eddy viscosity, for the Kolmogorov flow 234
Eddy viscosity, history 222—226
Eddy viscosity, negative 233 242
Eddy viscosity, renormalization group 237 240
Eddy viscosity, scale-dependent 237
Ekman friction 242
Electrolyte 250
Energy see also spectrum
Energy, balance equation 20 21
Energy, breakdown of conservation of 20
Energy, budget, scale-by-scale 21—26
Energy, cascade 98 104 115 239
Energy, conservation 20 174 246 249
Energy, cumulative 25
Energy, dissipation 26 67—71 75 76 88 180 188
Energy, dissipation rate 90 92 98 102 129
Energy, divergence of total 212 239
Energy, equipartition 209
Energy, finite dissipation of 57 103 129 244
Energy, flux 25 80 79—83 101 105 138 140 220
Energy, in terms of velocity increments 81
Energy, injection 26
Energy, inverse cascade of 84 114 196 233 242 242
Energy, law of decay of 112—115
Energy, local 159 159—165 178
Energy, mean 20 86
Energy, mean dissipation of 20
Energy, mean kinetic 53
Energy, of interaction of vortices 244
Energy, physical-space 78
Energy, redistributed among scales 22
Energy, transfer 83 83 115 211 220
Energy-containing eddies 105 219
Enstrophy 20; see also cascade
Equality in law 47
| Ergodicity 35 37 49 58 248
Euler equation 18 116 200 247; Hamiltonian
Euler equation as geodesic flow 202
Euler equation, symplectic structure 203
Euler equation, well-posedness 116
Eulerian correlation time 215
Extended self-similarity (ESS) 131 158
external noise 204
F(X) 160 161 162;
Fast variables 227
Feynman graphs see diagrammatic methods
Feynman integrals see functional integrals
Filaments (2-D) 249
Filtering, band-pass 101 126
Filtering, high-pass 22 122
Filtering, low-pass 22 52 80
Five-thirds law see spectrum (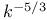 ) )
Flatland 251
Flatness 41 122 124—126
Flatness of velocity derivative 111 190;
Flatness, hyper- 129
Forster — Nelson — Stephen (FNS) theory see renormalization group
Four-fifths law 76 76—89 128 197 198
Four-fifths law, deviations from 129
Four-fifths law, implies 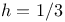 89 89
Four-fifths law, implies 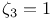 133 133
Four-fifths law, Kolmogorov's derivation 97
Fourier space 16
Fourth-cumulant-discard approximation see quasi-normal approximation
Fractal attractor 38
Fractal dimension 136 138 161
Fractal dimension, capacitary 137
Fractal dimension, capacity 137
Fractal dimension, correlation 161
Fractal dimension, covering 137
Fractal dimension, Hausdorff 137 138 180 200
Fractal dimension, information 161
Fractal dimension, negative 137
Fractal dimension, Renyi 160 181
Fractals 205
Fractals, convoluted coastlines 180
Fractals, due to level crossing 205
Fractals, lacunarity 130
Functional and diagrammatic methods 212 217
Functional integrals 212
Galerkin truncation 242
Galilean invariance 17
Galilean invariance, broken by forcing 87 232
Galilean invariance, random 17 87 212 215
Gaussian see random variable random
Gaussian integration by parts 43
Geometry 202
Global regularity 200
GOY see shell models
Great Red Spot 249
Green's function 213
Grid turbulence 8 73 95 111 134
Guiding-center approximation 241
Hamiltonian formulation, Euler equation 203
Hamiltonian formulation, point vortices 244 245 249
Hamiltonian formulation, tracer dynamics 204
Heat equation 226
Heat flux 226 229
Helicity 19 21 189 232;
Helium facility 65 130 158
Henon map 38
histogram 29
Hoelder continuity 99 200
Homogenization see multiscale methods
Hopf's equation 207—212
Hyperviscosity see dissipativity
Inertial range 62 86
Inertial range, practical determination of 129
Inertial range, span of 107
Infrared 54 105
Infrared cutoff 55
Infrared divergence 212
Integral scale 50
Intermediate dissipation range see multifractal model
Intermittency 120—194 194; singularities
Intermittency and vortex filaments 183 192
Intermittency factor 139
Intermittency in shell models 175—178
Intermittency in the dissipation range 125—126
Intermittency of local dissipation 162
Intermittency vs self-similarity 121 125
Intermittency, exact results 133—135
Intermittency, experimental data 127—133
Intermittency, external 96
Intermittency, not captured by closure 220
Intermittency, not disrupted by power-law forcing 239
Intermittency, revealed by high-pass filtering 125
Intermittency, small-scale 122
Intermittency, spurious 216
Invariant measure 34 35 38
Irrelevant term 238
Jeans — Vlasov — Poisson equation 245
K41 74 75 72—99 104 139 140 145 211 239
K41 and fractal level crossing 205
K41 and the correlation of the dissipation 216
K41 and the Richardson cascade 106
K41, consistent with anomalous correlation of the dissipation 216
K41, consistent with Burgers' equation 216
K41, consistent with cumulant hierarchy 211
K41, consistent with dissipation-range intermittency 126
K41, consistent with Richardson's diffusion law 102
K41, corrections to 104 106 127 133 172 180
K41, effect of viscosity 91—93
K41, historical remarks 98—99
K41, Landau's remark on 94—98 178 219
K41, renormalization group approach 238—240
K41, requires a chaotic cascade 116
K41, requires self-similarity 121
K41, structure functions 127
K41, universality 75 92 152—154
K41, viscous correction at inertial-range scales 216
Karman street see vortices (Karman)
Karman — Howarth — Monin relation 78
Knudsen number 225
Kolmogorov 1941 theory see K41
Kolmogorov flow 234 250
Kolmogorov — Arnold — Moser (KAM) tori 232
kurtosis see flatness
Lagrange multiplier 202 247
Lagrangian 214
Lagrangian history direct interaction approximation (LHDI) 219
Lagrangian turbulence see chaotic advection
Lagrangian, autocorrelation time 231
Lagrangian, coordinates 215
Lagrangian, derivative 116 201
Landau see K41
Large deviations 51 148 168—171 181
Large-scale, dynamics 230
Large-scale, equation 229
Large-scale, instability 233 234
Law of Large Numbers 49
Legendre transformation see multifractal model
Level crossing 205
Local dissipation 21
Localness of interactions 87 104 105 212 220
Localness of interactions, is it related to Galilean invariance? 219
Localness of interactions, not true in two dimensions 242
Log-Hopf equation 210
Log-periodic corrections to scaling 130 131
Log-Poisson model 190
Logarithmic law (von Karman) 225
Logistic map 31
Lognormal model 132 171 171—173
Lognormal model, exponent  165 165
Lognormal model, incorrectly derived by central limit theorem 173
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -model
-model 
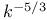 law
law