|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| O'Neill B. Ч The Geometry of Kerr Black Holes |
|
|
 |
| ѕредметный указатель |
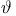 -equation 183 -equation 183
4-velocity 35
Acceleration 15
Achronal set 171Ч172
Action (of a Lie group 6Ч7
Allowed region, in an r-L plot 214
Analytic function 8
Analytic manifold 8
Angle function A for Kerr coordinates 80 122
Angular momentum of a geodesic around the Kerr axis 179
Angular momentum, per unit mass, of Kerr spacetime 58
Asymptotic flatness 59
Axial symmetry 59
Axis (of Kerr spacetime) 63 68
Axis (of Kerr spacetime), abstract 140 143
Axis (of Kerr spacetime), geometry of 87Ч88 102
Backward isometry 59 110 152Ч154 155Ч160 162Ч163
Barrier, in an r-L plot 230
Basis Hodge 303
Basis orthonormal 26
Basis positively oriented 303
Basis Theorem 3
Bianchi identity 19 341
Bianchi identity, in Newman Ч Penrose formalism 341Ч342
Biskew (0, 4) tensor 298
Bivector 360
Bivector decomposable 362
Bivector principal null 318
Black holes see under УSchwarzschild and KerrФ
Bound orbit see under УOrbit types and Global trajectoriesФ
Boyer Ч Lindquist (co)frame field 90Ч91
Boyer Ч Lindquist (co)frame field, brackets 96
Boyer Ч Lindquist (co)frame field, connection forms 92
Boyer Ч Lindquist (co)frame field, covariant derivatives 95
Boyer Ч Lindquist (co)frame field, curvature forms 98
Boyer Ч Lindquist (co)frame field, signs for 90 92
Boyer Ч Lindquist blocks 65Ч67
Boyer Ч Lindquist blocks, canonical imbedding of 82
Boyer Ч Lindquist blocks, causal properties of 75Ч78
Boyer Ч Lindquist blocks, incompleteness of block III 101
Boyer Ч Lindquist blocks, stationary properties of 70Ч72
Boyer Ч Lindquist blocks, visualization 63
Boyer Ч Lindquist coordinates 57
Boyer Ч Lindquist coordinates, failure at horizons 74
Boyer Ч Lindquist coordinates, metric identities for 60
Boyer Ч Lindquist polynomial 282
Boyer, R.H. 121
Bracket operation (Lie bracket) 5
Bracket operation (Lie bracket), for the Boyer Ч Lindquist vector fields 96
Bracket operation (Lie bracket), in Newman Ч Penrose formalism 334
Brans, Carl 348
Bundle structure of Kerr spacetime 140Ч144
Caesar, Julius 56
Canonical frame 323
Canonical imbedding of blocks 82
Canonical Kerr vector fields 60 68
Cartan computations, for the Boyer Ч Lindquist frame field 90Ч99
Cartan computations, in general 49Ч55
Carter band, in an r-L plot 236
Carter constant  183 183
Carter constant  and and 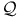 and approach to the ring singularity 201 and approach to the ring singularity 201
Carter constant  and and 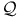 , effect on forbidden regions 217 , effect on forbidden regions 217
Carter constant  and and 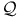 , effect on latitudinal motion 203Ч207 , effect on latitudinal motion 203Ч207
Carter constant  and and 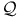 , general properties of 186Ч188 , general properties of 186Ч188
Carter constant 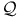 188 188
Carter's (first-integral) theorem 183
Carter's (first-integral) theorem, proof of 357Ч359
Carter, Brandon 78 183 288
Causal (nonspacelike) vector 29
Causal character of a curve, vector field 33
Causal character of a submanifold 46
Causal character of a subspace 29
Causal character of a vector 27
Causal character of Boyer Ч Lindquist coordinate vector fields 66 70Ч72 78
Causal character of the canonical vector fields 66Ч67 see УNullФ УSpacelikeФ
Causal spacetime 75
Causality 74Ч75 171
Central sphere 69 145
Chandrasekhar, S. 349
Christoffel symbols 15
Chronological future [past] set 171
Chronological spacetime 75 174
Chronology 171
Chronology of Kerr spacetimes 171Ч176
Circular coordinate 7Ч8
Closed submanifold 43
Coframe field 11
Colatitude 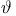 43Ч44 43Ч44
Colatitude 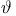 , as Boyer-Lindquist coordinate 57Ч58 , as Boyer-Lindquist coordinate 57Ч58
Colatitude 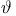 , as coordinate of a geodesic 201Ч207 , as coordinate of a geodesic 201Ч207
Comparison of Schwarzschild and Kerr spacetimes see УSchwar schild comparisonФ
Complete vector field 6
Components of tensors 10 11
Configuration of an r-L plot see under Уr-L plotФ
Conformal flat spacetime 314
Congruence 45 see
Connection forms 50Ч52
Connection forms for the Boyer Ч Lindquist frame field see under УBoyer Ч LindquistФ
Conservation lemma 20
Continents, in an r-L plot 223
Contraction of tensors 11Ч12 17 299 332Ч333
Coordinate function 2
Coordinate neighborhood 2
Coordinate one-form 6
Coordinate system 2
Coordinate vector 3 5
Covariant derivative 14Ч15
Covariant derivative in Newman Ч Penrose formalism 334
Covariant derivative of Boyer Ч Lindquist vector fields 94Ч95
Covector 6
Crossing spheres 119 121 130 135 138 140 146
Curvature form 52
Curvature of Kerr spacetime, Cartan computation 96Ч100
Curvature of Kerr spacetime, Newman-Penrose expression 3
Curvature singularity 101
Curvature transformation 300
Curvature, abstract 298
Curvature, Gaussian 19 54
Curvature, in Newman-Penrose terms 338Ч340
Curvature, Kretschmann 18
Curvature, relativistic significance of 35Ч36
Curvature, Ricci 18
Curvature, Riemannian 17Ч19
Curvature, scalar 18
Curvature, sectional 18
Curvature, symmetries of 18
Curvature, Weyl conformal 301
Curve 4
Cyclic symmetry 298
Deformation retract 164
Diffeomorphism 3
Differential forms 6 355Ч356
Differential map 4
Differential of a function 6
Dimension of a manifold 2
Discriminant polynomial 215 217Ч222
distribution 44Ч45
Distribution, integrability of 45
Dual basis (or coframe) 11
e-Q chart 219Ч220
Effective energy, of a geodesic 214
Effective potential, for axial geodesics 254
Effective potential, for polar geodesics 263
Effective potential, in the 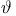 -equation 201Ч202 -equation 201Ч202
Einstein manifold 308 311
Einstein summation convention (weak) 10
Einstein, Albert 31 33 35
Energy extraction from a black hole 181Ч182
Energy, of a particle in Kerr spacetime 179
Energy-momentum 4-vector 35
| Equator (equatorial plane) 68 146Ч147
Equatorial geodesics 272Ч287
Equatorial geodesics, circular null 277Ч278
Equatorial geodesics, circular timelike 282Ч283
Equatorial geodesics, in r<0 273Ч274
Equatorial geodesics, longitudinal motion of 283Ч284
Equatorial geodesics, null 276Ч279
Equatorial geodesics, spacelike 285Ч286
Equatorial geodesics, timelike 279Ч283
Equatorial isometry 68
Ergosphere 72Ч73 181
Escape energy 211
Euclidean space 2
Euler equations 16
Event 32
Event horizon 86Ч87
expansion see under УOptical scalarsФ
Extension of Kerr spacetimes 57
Extension of manifolds by coordinates 20Ч21
Extention of Kerr spacetimes across r=0 62
Extention of Kerr spacetimes over the axis 64
Extention of Kerr spacetimes, plan for 105 see
Extention of manifolds by gluing 21Ч25
Exterior derivative 356
Exterior of Kerr spacetime 66
Exterior product of forms and of vectors see Уwedge productФ
Exterior product of vector spaces 299 361Ч364
Fiber bundle 7
Fiber spheres 144
Fiber spheres in horizons 145Ч146
First structural equation 50
First-integrals 178Ч179 183
First-integrals as coefficients of the polynomial R(r) 208
First-integrals effect on orbits 222Ч235
Flat manifold 36
Flow 6
Flyby orbit see under УOrbit types and Global trajectoriesФ
Foliation 45
Forbidden region, in an r-L plot 214
Frame field 10Ч11
Frame field, Boyer Ч Lindquist see under УBoyer-LindquistФ
Frame field, orthonormal 17
Frobenius' Theorem 44 356
Fundamental groups of Kerr spacetimes 165 167 170
Future set see УChronological future setФ
Future [past] complete geodesic 111
Future [past] side 172
Future-pointing 33
Futurecone 33
g-null 318
General relativity, introduction to 31Ч42
Geodesic completeness 15
Geodesic completeness modulo the ring singularity 189
Geodesics 15Ч16 48 334
Geodesics complete 111
Geodesics in Kerr spacetime, axial 250Ч255
Geodesics in Kerr spacetime, equations for: Colatitude equation (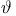 -equation) 183 -equation) 183
Geodesics in Kerr spacetime, equations for: Coordinate integral equations 190 191
Geodesics in Kerr spacetime, equations for: First-order equations for longitude and time 181 190
Geodesics in Kerr spacetime, equations for: Radial equation (r-equation) 183
Geodesics in Kerr spacetime, extensions of, across horizons 196Ч200
Geodesics in Kerr spacetime, extensions of, through a Boyer-Lindquist block 195
Geodesics in Kerr spacetime, hitting the ring, singularity 101
Geodesics in Kerr spacetime, hitting the ring, via the equator 288
Geodesics in Kerr spacetime, in horizons 255Ч262
Geodesics in Kerr spacetime, initial data for 185
Geodesics in Kerr spacetime, polar 262Ч272
Geodesics in Kerr spacetime, regular 189
Geodesics in Kerr spacetime, with Q=0 287Ч291 293 see УFirst-integralsФ УGlobal УPrincipal
Geometric units 351Ч353
Global trajectories, of Kerr geodesics 243Ч250
Global trajectories, of Kerr geodesics, for standard particles 244
Global trajectories, of Kerr geodesics, timelike bound orbits: in block I 247
Global trajectories, of Kerr geodesics, timelike bound orbits: in block III 247
Global trajectories, of Kerr geodesics, timelike bound orbits: large 248Ч249
Global trajectories, of Kerr geodesics, timelike flyby orbits: exterior 245
Global trajectories, of Kerr geodesics, timelike flyby orbits: in block III 245
Global trajectories, of Kerr geodesics, timelike flyby orbits: long 245Ч247
Global trajectories, of Kerr geodesics, timelike transit orbit 249Ч250
Gluing data 21
Gluing of manifolds 21Ч25
Goldberg Ч Sachs theorem 345Ч348
Hausdorff condition (for gluing) 23Ч24
Hitting the ring singularity see under УGeodesics in Kerr spacetimeФ
Hodge basis 303
Hodge double indices 304 310
Hodge identity 304
Hodge star operator 303Ч308
Hodge star operator, as complex structure 305
Hodge star operator, in complex scalar product 306
Homotopy equivalence 164
Homotopy type 164
Homotopy type of extreme Kerr spacetime 168
Homotopy type of fast Kerr spacetime 164Ч165
Homotopy type of slow Kerr spacetime 166Ч168
Homotopy type of small Kerr spacetimes 168Ч170
Horizon function  58 62 58 62
Horizon sphere 145
Horizon, in Kerr spacetime 58 62Ч63
Horizon, in Kerr spacetime, as one-way membrane 84 172
Horizon, in Kerr spacetime, crossing, by geodesics 196Ч200
Horizon, in Kerr spacetime, geometry of 83Ч85
Horizon, in Kerr spacetime, long see УLong horizonФ
Hypersurface 42Ч43 45Ч46 48
Hypersurface, achronal 171
Hypersurface, one-and two-sided 46
Hypersurface, separating 46
Hypersurface-orthogonal vector field 48 71 356
Index of a scalar product 26
Inextendibility of Kerr spacetimes 293Ч295
Inner product 12
Instantaneous observer 38
Integral curve 5
Integral manifold 44Ч45
Isometries of Boyer Ч Lindquist blocks 149Ч154
Isometries of extreme Kerr spacetime 155Ч158
Isometries of Kruskal domains 158Ч160
Isometries of slow Kerr spacetime 161Ч163
Isometry 13Ч14 48
Jacobi identity 5
KBL coordinates 121Ч130
KBL coordinates, related to Boyer Ч Lindquist coordinates 131Ч132 137
Kerr black hole see also УKerr spacetimeФ
Kerr black hole, overview 55Ч56
Kerr black hole, physical properties summarized 102Ч103
Kerr exterior (block I) 66
Kerr metric on 131 134Ч135
Kerr metric tensor (or line-element), compared with Minkowski and Schwarzschild metrics 58
Kerr metric tensor (or line-element), in Boyer Ч Lindquist coordinates 58Ч59
Kerr metric tensor (or line-element), in Boyer Ч Lindquist coordinates, alternative formulation of 91
Kerr metric tensor (or line-element), in KBL coordinates 134Ч135
Kerr metric tensor (or line-element), in Kerr-star coordinates 81
Kerr metric tensor (or line-element), in star-Kerr coordinates 107
Kerr metric tensor (or line-element), on Kruskal domains 131Ч135
Kerr metric tensor (or line-element), on the axis 64Ч65
Kerr metric tensor (or line-element), Petrov type D character of 315Ч317
Kerr observers 71Ч74
Kerr patch 114 138
Kerr spacetime, maximal analytic extensions of see УMaximal Kerr spacetimesФ
Kerr spacetime, slow, extreme, fast see УRotation typesФ
Kerr spacetime, working definition of 67Ч68
Kerr, Roy 31
Kerr-Newman metric 61
Kerr-star spacetime 79Ч83
Kerr-star spacetime, definition 82
Killing isometry (group) 149Ч150
Killing orbit 69
Killing vector field 19Ч20 48
Killing vector field on Kerr spacetime 59 68 69 70Ч71 155
Kinnersley, William 344
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



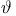 -equation
-equation 
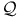 and approach to the ring singularity
and approach to the ring singularity 