|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rivano N.S. — Categories Tannakiennes |
|
|
 |
| Предметный указатель |
 -groupe anisotrope, compact V 0.3.2 -groupe anisotrope, compact V 0.3.2
 -groupe hodgien V 2.7.2 -groupe hodgien V 2.7.2
 -groupe polarisable V 2.7.1 -groupe polarisable V 2.7.1
 -categorie I 0.1.1 -categorie I 0.1.1
 -categorie A-lineaire I 0 -categorie A-lineaire I 0
 -categorie AC, AU, CU, ACU I 2.1.1 2.2.1 2.3 2.4.1 -categorie AC, AU, CU, ACU I 2.1.1 2.2.1 2.3 2.4.1
 -categorie associative I 1.1.1 -categorie associative I 1.1.1
 -categorie commutative I 1.2.1 -categorie commutative I 1.2.1
 -categorie opposee I 0.1.4 -categorie opposee I 0.1.4
 -categorie rigide I 5.1.1 -categorie rigide I 5.1.1
 -categorie symetrique I 0.1.4 -categorie symetrique I 0.1.4
 -donnee de descente III 1.3.5.1 -donnee de descente III 1.3.5.1
 -equivalence I 4.4.1 -equivalence I 4.4.1
 -filtration admissible IV 2.2.1 -filtration admissible IV 2.2.1
 -filtration centrale IV 2.2.6 -filtration centrale IV 2.2.6
 -filtration de type unipotent IV 2.5.2.2 -filtration de type unipotent IV 2.5.2.2
 -filtration exacte IV 2.1.1 -filtration exacte IV 2.1.1
 -filtration localement scindable IV 2.2.1 -filtration localement scindable IV 2.2.1
 -filtration scindable IV 2.2.1 -filtration scindable IV 2.2.1
 -filtrations opposees IV 2.3.1 2.3.3 -filtrations opposees IV 2.3.1 2.3.3
 -foncteur I 4.1.1 -foncteur I 4.1.1
 -foncteur A-lineaire I 4.1.3 -foncteur A-lineaire I 4.1.3
 -foncteur AC, AU, CU, ACU I 4.2.4 -foncteur AC, AU, CU, ACU I 4.2.4
 -foncteur associatif I 4.2.1 -foncteur associatif I 4.2.1
 -foncteur commutatif I 4.2.2 -foncteur commutatif I 4.2.2
 -foncteur compatible avec les Horn I 4.3.1 -foncteur compatible avec les Horn I 4.3.1
 -foncteur rigide I 5.2.1 -foncteur rigide I 5.2.1
 -foncteur strict I 4.1.1 -foncteur strict I 4.1.1
 -foncteur unifere I 4.2.3 -foncteur unifere I 4.2.3
 -generateur II 4.3.1 -generateur II 4.3.1
 -graduation IV 1.2.2 -graduation IV 1.2.2
 -graduation centrale IV 1.2.2.1 -graduation centrale IV 1.2.2.1
 -morphisme I 4.1.1 -morphisme I 4.1.1
 -morphisme unifere I 4.2.3. -morphisme unifere I 4.2.3.
 -structure I 0.1.1 -structure I 0.1.1
 -structure A-lineaire I 0.1.2 -structure A-lineaire I 0.1.2
 -algebre II 1.0.2 -algebre II 1.0.2
 -algebre corepresentable II 1.2.1 -algebre corepresentable II 1.2.1
 -algebre des distributions (sur un A-monoide) II 3.0.2 -algebre des distributions (sur un A-monoide) II 3.0.2
 -algebre representable II 1.2.2 -algebre representable II 1.2.2
 -module II 1.0.2 -module II 1.0.2
 -module corepresentable II 1.1.1 -module corepresentable II 1.1.1
 -module representable II 1.1.1 -module representable II 1.1.1
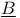 - - -categorie I 4.5.1.1 -categorie I 4.5.1.1
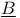 - - -categorie -categorie  -lineaire, -lineaire, 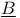 -lineaire I 4.5.4 -lineaire I 4.5.4
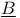 - - -categorie fibree I 4.5.5 -categorie fibree I 4.5.5
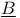 - - -foncteur I 4.5.3 -foncteur I 4.5.3
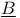 - - -morphisme I 4.5.3 -morphisme I 4.5.3
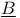 - - -morphisme unifere I 4.5.3 -morphisme unifere I 4.5.3
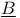 -categorie -categorie  -lineaire, -lineaire, 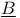 -lineaire I 4.5.4 -lineaire I 4.5.4
A-module (dans une  -categorie) I 6.2.1 -categorie) I 6.2.1
A-module unifere I 6.2.1
Adjoint (d'un morphisme) V 2.1.2.1 2.1.4
Algebre (dans une  -categorie) I 6.1.1 -categorie) I 6.1.1
Algebre commutative, associative, unifere, AC , AU , CU , ACU I 6.1.2
Algebre opposee I 6.1.1
Algebre produit tensoriel I 6.1.1
Bigebre (dans une  -categorie) I 6.1.3 -categorie) I 6.1.3
Categorie a petits objets II 2.3.1
Categorie A-lineaire I 0.1.2
Categorie des motifs VI 4.1.3.2 4.2.1.4
Categorie des motifs effectifs VI 4.1.2.2
Categorie ind-tannakienne III 1.1.1
Categorie ind-tannakienne neutre III 1.1.1.2
Categorie karoubienne VI 4.1.2.1
Categorie noetherienne, localement noetherienne II 2.3.4.2
Categorie tannakienne III 3.2.1
Categorie tannakienne algebrique III 3.3.1
Categorie tannakienne neutre III 3.2.1
Categorie tannakienne polarisable V 2.4.4
Categorie tannakienne polarisee V 2.4.5.1
Cogebre I 6.1.1.1
Cogebre coassociatlve, cocommutative, coUnifere I 6.1.2.2
Cohomologie 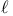 -adique VI A 1.4.1 -adique VI A 1.4.1
Cohomologie cristalllne VI A 1.4.5
Cohomologie de Bettl-Hodge VI A 1.4.4
Cohomologie de De Rham VI A 1.4.3
Cohomologie de Hodge VI A 1.4.2
Comodule (dans une  -categorie) I 6.2.2 -categorie) I 6.2.2
Comodule coplat II 2.4.3
Comodule counifere I 6.2.2
Contrainte AC, AU, CU, ACU I 2.1.1 2.2.1 2.3 2.4.1
Contrainte d'associativite I 1.1.1
Contrainte d'unite I 1.3.1
Contrainte de commutativite I 1.2.1
Contrainte de commutativite stricte I 1.2.3
Contrainte opposee, symetrique I 1.4
Contraintes cohomologues I 1.1.3 1.2.3
Coproduit tensoriel (de comodules) II 2.4.3
Correspondance algebrique VI A 0.3
Correspondance cohomologique VI A 1.3.2
Distributions (sur un monofde) II 3.0.2
Distributions de Dirac II 3.0.2
Donnee de descente (pour une categorie llneaire) III 1.2.1
Element hodgien (d'un  -groupe algebrique) V 2.7.2 3.3.1 -groupe algebrique) V 2.7.2 3.3.1
Enveloppe algebrique (d'un groupe topologique,) V 0.3.1
Enveloppe representable (d'un  -module) II 1.1.2.3 -module) II 1.1.2.3
F-cristal VI 3.1.1 3.1.3
| F-cristal isopentique VI 3.3.3.1
F-isocristal VI 3.1.3
Faisceau 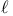 -adique VI 1.1.3 -adique VI 1.1.3
Filtration de Hodge VI 2.1.1.3 A
Filtration par les niveaux VI 4.3.2
Foncteur borne II 2.3.1
Foncteur fibre II 3.2.1 4.2
Foncteur fibre a valeurs dans un schema III 3.2.1.2
Foncteur relativement exact II 2.4.2
Forme bilineaire V 2.1.1
Forme bilineaire non degeneree V 2.1.1
Forme de C-polarisation V 2.7.1 3.3.1
Forme de Weil V 2.3.1 2.3.5
Forme positive (pour une polarisation) V 2.4.1 3.2.1
Forme sesquilineaire V 2.2.1
Forme sesquilineaire conjuguee V 2.2.5
Forme sesquilineaire non degeneree V 2.2.1
Formes de Weil compatibles V 2.3.1 2.3.5
G-module III 3.3.2
G-module fidele III 3.3.2
G-module, G-A-module II 3.0.3
Gerbe III 2.1.1
Gerbe neutre III 2.1.1.1
Gerbe tannakienne III 2.2.1
Gerbe tannakienne algebrique III 3.1.0
Graduation de type I IV 1.1.1
Graduation par le poids V 3.1.1
Groupe d'holonomie (d'un schema, d'un module stratifie) VI 1.2.2.1
Groupe d'holonomie (d'une categorie en un foncteur fibre) III 3.2.1.2
Groupe d'holonomie restreint (d'un schema, d'un module stratifie) VI 1.2.2.1
Groupe de Mumford — Tate (d'une structure de Hodge) VI 2.1.2.3
Inverse (pour un objet inversible) I 2.5.4
Inverse AU (pour un objet inversible) I 2.5.5.2
L-categorie ind-tannakienne III 2.3.3
L-gerbe III 2.1.4
Lien III 2.1.3
Lien abelien III 2.1.3
Lien algebrique III 3.1.4
Lien polarisable V 2.4.5.1 2.6.1.2
Lien reductif V 1.1.2
Lien representable III 2.1.3
Lineairement compact (espace vectoriel) II 1.4.1
Loi  I 0.1.1 I 0.1.1
Module stratifie VI 1.2.1
Morphisme d'unites I 1.3.4
Morphisme d'unites reduites I 1.3.2.2
Morphisme de categories tannakiennes III 3.2.1.1
Morphisme de foncteurs fibre II 3.2.1 4.2
Morphisme de Gysin VI A 1.1.1.8
Morphisme de theories de cohomologie VI A 1.1.2
Morphlsme de categories ind-tannakiennes III 1.1.1.1
Motif (d'une variete) VI 4.1.2.2
Motif de Lefschetz VI 4.1.2.4
Motif de Tate VI 4.1.3.2
Motif purement de niveau n VI 4.3.2
n-connexion VI 1.2.1
Niveau d'un motif VI 4.3.1
Niveau de Hodge VI A 5.2.1
Objet 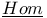 , , 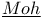 I 3.1.1 I 3.1.1
Objet de Tate V 3.1.1
Objet inversible I 2.5.0
Objet n-regulier (n = 0,1,2) I 0.1.3
Objet n-regulier a gauche, a droite I 0.1.3
Objet noetherien II 2.3.4.2
Objet reflexif I 3.2.3.3
Objet unite I 1.3.2
P-nombre de Weil VI 4.6.3.2
Parite (d'une forme non degeneree) V 2.1.2 2
Parite (d'une polarisation) V 2.4.1
Pente (d'un F-cristal) VI 3.3.3.1
Polarisation V 2.4.1 2.4.3 3.2.1
Polarisation hodgienne V 2.7.2 3.3.1
Polarisation symetrique V 2.4.1
Produit tensoriel externe II 1.5.1
Pseudo-generateur II 2.6.2
Quadruple de  -equivalence I 4.4.1 -equivalence I 4.4.1
Rang (d'un objet) I 5.1.4
Relation d'equivalence admissible VI A 0.2.1
Scindage (d'une  -filtration) IV 2.1.1 -filtration) IV 2.1.1
Signature (d'un objet inversible) I 2.5.3
Sous-categorie de definition II 2.2.1 3.4
Sous-objet isotrope, non isotrope, totalement isotrope V 2.1.6
Sous-objet orthogonal (a un sous-objet) V 2.1.6
Stratification VI 1.2.1
Structure A-lineaire I 0.1.2
Symetrie canonique I 1.2.3
Systeme local VI 1.1.1
Systeme local 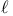 -adique VI 1.1.3 -adique VI 1.1.3
Theorie de cohomologie VI A 1.1 1.1.5
Trace (d'un endomorphisme) I 5.1.4
Transpose (d'un endomorphisme) V 2.1.2.1
Transpose (d'un morphisme) V 2.1.4
Triple de Tate V 3.1.1
Triple de Tate neutralise V 3.1.3
Triple de Tate neutre V 3.1.3
Triple de Tate polarisable V 3.2.2.1
Unite (pour une  -categorie) I 1.3.1 -categorie) I 1.3.1
Unite a gauche, a droite, bilatere I 1.3.1.3
Unite reduite I 1.3.2
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -groupe anisotrope, compact
-groupe anisotrope, compact  -categorie
-categorie  -algebre
-algebre 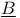 -
- -lineaire,
-lineaire, 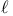 -adique
-adique 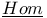 ,
,