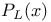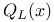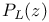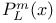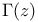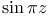|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wyld H.W. — Mathematical Methods for Physics |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Aerodynamics 7 9
Analytic continuation 435—440
Analytic continuation, of Fourier integrals 581—587 596ff.
Analytic continuation, of gamma function 440—442
Analytic continuation, of hypergeometric function 528—531
Analytic functiony definition 386
Asymptotic expansions 513—516
Asymptotic expansions, for 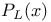 83 83
Asymptotic expansions, for 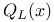 91 91
Asymptotic expansions, for Bankel functions 133 215 552—560
Asymptotic expansions, for Bessel functions of imaginary argument 135
Asymptotic expansions, for Bessel functions. 133 215 552—560
Asymptotic expansions, for exponential integral 514—515
Asymptotic expansions, for gamma function 516—519
Asymptotic expansions, for hypergeometric function 531
Asymptotic expansions, for Neumann functions 133 215 552—560
Asymptotic expansions, for spherical Bessel, Neumann, and Hankel functions 183—184 216
Ausstrahlungsbedingimg see “Radiation condition”
Bernoulli numbers 443
Bessel functions 34 36 123—126 214 541—552
Bessel functions, asymptotic expansions 133 135 215 556—560
Bessel functions, generating functions for 152 547
Bessel functions, identities for 152
Bessel functions, integral representation for 550
Bessel functions, of imaginary argument 134—135
Bessel functions, series for 125 552
Bessel functions, small argument expansions 132 214
Bessel functions, Sommerfeld’s integral representation for 546
Bessel functions, spherical Bessel functions 178—184 215—216
Bessel’s equation 33—34 36 123 214 542
beta function 509—510
Boundary conditions for Bessel functions 139
Boundary conditions for dielectrics 227—229
Boundary conditions for diffusion equation 155 210 319 320 322
Boundary conditions for drumhead 163
Boundary conditions for Helmholtz equation 156—157 210
Boundary conditions for inhomogeneous ordinary differential equations 261—262 270
Boundary conditions for Laplace’s equation 110—113 211—212
Boundary conditions for Legendre polynomials 77
Boundary conditions for magnetic media 246
Boundary conditions for Poisson’s equation 273 274
Boundary conditions for spherical Bessel functions 184
Boundary conditions for spherical harmonics 96
Boundary conditions for Sturm Llouville equation 49—50
Boundary conditions for wave equation 159 210 300 303 “Radiation
Branch point 405 409 410 412 414 416
Cauchy — Riemann equations 392
Cauchy’s integral formula 426—428
Cauchy’s Theorem 421—423 423—425
Cerenkov effect 315
Circle chain method 436—439
Completeness relations for Fourier integrals 60 212
Completeness relations for Fourier — Bessel transforms 213
Completeness relations for Legendre polynomials 85
Completeness relations for spherical Bessel functions 187 214
Completeness relations for spherical harmonics 99
Completeness relations for Sturm Liouville problem 57
Contour integrals 417—421 448—465
Convergence, absolute 395
Convergence, Cauchy criterion 395
Convergence, of power series 398—400
Convergence, of series 395ff.
Convergence, ratio test for 396
Convergence, uniform 428
Cut in complex plane 406 407 409 410 412 414 416 486—487 530—531 534—535 538—539 601 606
Differential equations, ordinary 38—57
Differential equations, ordinary, indicial equation 45 76 123
Differential equations, ordinary, ordinary points 39
Differential equations, ordinary, second solution 42 47 88ff. 126ff.
Differential equations, ordinary, series solution 43—49 75—80 123—126
Differential equations, ordinary, singular points 39 75 123 519—522
Differential equations, ordinary, with constant coefficients 588—590
Differential equations, ordinary, with three regular singular points 519ff.
Differential equations, ordinary, Wronskian 40—42 47 152 288
Differential equations, partial see “Diffusion equation” “Helmholtz “Klein “Laplace’s “Poisson’s “Wave
Diffusion equation 2—4 29 155 166—168 209 319—326
Dipole moment 105—106 223
Dirac’s formula 479
Discontinuity problem 479—481
dispersion relation 481—492
Dispersion relation, subtracted 490—491
Eigenfunctions, eigenvalues, for angular part of Laplaclan 96
Eigenfunctions, eigenvalues, for Helmholtz equation 156—158 210
Eigenfunctions, eigenvalues, for integral equations 341 343 346 354 361—363 368—374
Eigenfunctions, eigenvalues, for Legendre’s equation 83 93
Eigenfunctions, eigenvalues, for particle in cylindrical box 168
Eigenfunctions, eigenvalues, for spherical Bessel functions 184—187
Eigenfunctions, eigenvalues, for Sturm Liouville problem 49—57
Eigenfunctions, eigenvalues, for vibrating string 161—162
Eigenfunctions, eigenvalues, for.vibrating drumhead 162—166
Eigenfunctions, eigenvalues, numerical solution for 64—66 354
electric field 15ff.
Electric field, macroscopic 219ff.
Electrodynamics 14—21 298 313—318
Electromagnetic field, due to point source 311—318
Essential singularity 434
Euler’s constant 129 132 512
Expansion theorems, for associated Legendre polynomials 93
Expansion theorems, for Bessel functions 140—141 213
Expansion theorems, for Legendre polynomials 84
Expansion theorems, for plane wave in cylindrical waves 152 547
Expansion theorems, for plane waves in spherical waves 187—189 217 338
Expansion theorems, for spherical Bessel functions 186 213
Expansion theorems, for spherical harmonics 99
Expansion theorems, for spherical waves in spherical waves about displaced center 189—192 217 338
Expansion theorems, for Sturm — Liouville problem 55—57
Expansion theorems, Fourier Bessel transforms 150 213
Expansion theorems, Fourier integral theorem 60 212
Expansion theorems, Fourier series 59 212
Fourier Bessel transforms 149—151 186 213 214
Fourier integral transforms 59—60 212
Fourier series 58—59 212
Fredholm’s solution of integral equation 356—363
Fredholm’s solution of integral equation, conditions for validity of 363—368
Gamma function 128—130 440—442 508—512 516—519
Gauge transformations 17 19—20
Generating functions for Bessel functions 152 547
Generating functions for Legendre polynomials 86 217
Green’s function, advanced 309
Green’s function, expansion in eigenfunctions 269—272 289—291
Green’s function, for bowed string 265—268
Green’s function, for diffusion equation 319—326
Green’s function, for Helmholtz equation 283—291 566—570
Green’s function, for ingoing waves 293
Green’s function, for Klein — Gordon equation 573—530
Green’s function, for ordinary differential equations 260—264
Green’s function, for outgoing waves 293 337
Green’s function, for Poisson’s equation 272—283
Green’s function, for scattering problem 337
Green’s function, for wave, equation 291—310 570—572
Green’s function, retarded 297 301ff. 304—306 311
Green’s Theorem 259 272 301 303 320 322
Hankel functions 133
Hankel functions, asymptotic expansions 133 215 556—560
Hankel functions, Sommerfeld’s integral representations for 544ff.
Hankel functions, spherical Bankel functions 182 183 215 216
Heat conduction equation see “Diffusion equation”
Helmholtz equation 29 30 32 34 154 156—158 163 169 171 177
Helmholtz equation, as eigenvalue problem 156—158
Helmholtz equation, eigenfunctions for 157
Hilbert transforms 483
Hilbert — Schmidt theory 368—374
Hydrodynamics 7ff. 11ff. 115—117
Hypergeometric functions 402 519—532
Hypergeometric functions, confluent 532
Hypergeometric functions, Legendre functions expressed as 537 541
Hysteresis 252
Identity theorem for analytic functions 436—437
Images, for Qrefen’s function 276—279
Images, magnetostatics 253ff.
| Images, method of electrostatics 230ff.
Initial conditions for diffusion equation 155 210 319 320 322 323 326
Initial conditions for Klein — Gordon equation 574
Initial conditions for vibrating membrane 165
Initial conditions for vibrating string 162
Initial conditions for wave equation 159 211 300 301 303 304 309—310 571—572
Integral equations, convolution equations 347—348 590 591—592
Integral equations, eigenvalue problem 341 343 345 354 361—363 368—374
Integral equations, first kind 341
Integral equations, for scattering problem 337 340 350
Integral equations, Fredholm formulas 356—363
Integral equations, Hilbert — Schmidt theory 368—374
Integral equations, numerical solution 351—356
Integral equations, second kind 341 342 344 347 349 353 356 361
Integral equations, separable kernels 342—347
Integral equations, singular, with Cauchy kernels 499—505
Integral equations, Volterra 341
Integral transforms, Fourier 60 212 565ff.
Integral transforms, Fourier Beaael 149—151 186 213 214
Integral transforms, Fourier, ohe-sided 581—587
Integral transforms, Hilbert 483
Integral transforms, Laplace 587—590 593—596
Integral transforms, Mellin 590—592
Integrals, angular 462—464
Integrals, evaluation 448—465
Integrals, on range 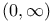 459—462 459—462
Integrals, rational functions 451—453
Integrals, transformation of contour 464—465
Integrals, with exponential factors 453—459
Irrotational flow 11 115—117
Iteration of integral equation see “Liouville — Neumann series”
Jordan’s lemma 453—455
Klein — Gordon equation 573
Laplace’s equation 108—117 211
Laplace’s equation, between two planes 147—149 151
Laplace’s equation, cylinder in external field 145—147
Laplace’s equation, exterior problem for cylinder 144
Laplace’s equation, exterior problem for sphere 112
Laplace’s equation, flow around sphere 115—117
Laplace’s equation, for dielectric sphere 233—235
Laplace’s equation, interior problem for cylinder 136—139 141—143
Laplace’s equation, Interior problem for sphere 110
Laplace’s equation, sphere in external field 113—115
Laurent expansion 433
Legendre functions 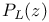 533—537 533—537
Legendre functions  37 88—92 497/538—541 37 88—92 497/538—541
Legendre functions  , identity for 562 , identity for 562
Legendre polynomials 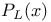 37 78—87 37 78—87
Legendre polynomials 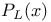 , formulas 80 81 , formulas 80 81
Legendre polynomials 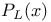 , generating function for 86 , generating function for 86
Legendre polynomials 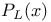 , identities for 86 87 92 119 , identities for 86 87 92 119
Legendre polynomials 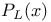 , normalization 81 84 , normalization 81 84
Legendre polynomials, associated, 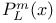 92—95 92—95
Legendre polynomials, formulas 93 95 217
Legendre polynomials, normalization 95
Legendre’s equation 37 75 77 88 533
Liouville — Neumann series 348—351
Liouville — Neumann series, convergence of 365
Liouyille’s theorem 445
Magnetic field 15ff.
Magnetic field, macroscopic 241ff.
magnetic moment 240
Magnetic pole density 250
magnetization 244 247ff. 250ff.
Magnetization, current 241—245 248—249
Maximum modulus theorem 445
Maxwell’s equations 15
Mean value theorem 444
Morera’ s theorem 421—423
Multipole expansion for scalar potential 103—108
Multipole expansion for vector potential 236—240
Natural boundary in complex plane 439
Neumann functions 34 36 126—131 214 546
Neumann functions, series for 131
Neumann functions, spherical Neumann functions 178—184 215
Normal modes, for acoustic resonant cavity 168—170
Normal modes, for acoustic wave guide 170—173
Normal modes, for vibrating drumhead 162—166
Normal modes, for vibrating string 161—162
Numerical solution, integral equations 351—356
Numerical solution, ordinary differential equations 61—66
Omnes’ equation 500ff.
Partial fraction expansions 466—470
Plasma dispersion function 497—499
Plemelj formulas 476—479
Poisson’s solution of Dirichlet problem for circle 446—447
Polarization 224 226
Polarization, charge 220—227 229 232 235
Pole in complex plane 39 390 434
Polsson’s equation, scalar 16 103 272—283
Polsson’s equation, vector 17
Potential, scalar 15 19 103 219ff.
Potential, vector 16 18 236ff.
Power series 43ff. 78 123 397—402
Product expansions for 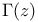 512 512
Product expansions for 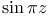 470 470
Quadrupole moment 106) 223
Radiation condition 195 294 310 336—337 568—570 605
Rational functions 389
Regular function see “Analytic function”
Residue theorem 448—451
Riemann sheets 407 408 409 412 415 417 492
Rlemann P symbol 522ff.
Rodrlgue’s formula 80
Runge — Kutta numerical integration 62f f.
Scattering, in quantum mechanics 336—340 550—351
Scattering, of waves by sphere 197—203
Schrodinger’s equation 4 160 168
Schwartz reflection principle 487—489
Separation of variables 29—38 207—269
Separation of variables, Helmholtz equation, cartesian coordinates 30
Separation of variables, Helmholtz equation, cylindrical coordinates 32
Separation of variables, Helmholtz equation, spherical coordinates 34
Separation of variables, Laplace’s equation 34 36
Separation of variables, spherical harmonica 75
Separation of variables, time dependence 29 156 160
Small argument expansions for Bessel functions 132 214
Small argument expansions for Bessel functions of imaginary argument 135
Small argument expansions for Neumann functions 132 214
Small argument expansions for spherical Bessel and Neumann functions 183 216
Sommerfeld — Watson transformation 471
Spectral representation 484
Spherical harmonics 96—103 104ff. 109ff. 178 189 192 194ff. 198ff. 216—217
Spherical harmonics, addition theorem 99—103 217
Spherical harmonics, completeness 99
Spherical harmonics, formulas 96—98 216—217
Spherical harmonics, normalization 98—99
Steepest descents, method of 516—519 552—560
Stirling’s formula 518 519
Sturm — Liouville problem 49—57
Sturm — Liouville problem, completeness of solutions 54—57
Sturm — Liouville problem, for associated Legendre polynomials 93—95
Sturm — Liouville problem, for Bessel functions 139—141
Sturm — Liouville problem, for legendre polynomials 83—84
Sturm — Liouville problem, for spherical Bessel functions 184—187
Sturm — Liouville problem, orthogonality of solutions 54
Sturm — Liouville problem, relation to Green’s function 269—272
Taylor expansion 430
Wave equation 159 209 291—310
Wave equation, acoustic 9 168—170 170—173
Wave equation, for electromagnetic fields 18
Wave equation, for membranes 6 162—166
Wave equation, for scalar potential 20 298
Wave equation, for strings 5 161—162
Wave equation, for vector potential 20 298
Wave guide, acoustic 170—173
Waves, acoustic 9 168—170 170—173
Waves, diffraction by knife edge 604—617
Waves, due to point source 311—318
Waves, emission of spherical wave 192—197
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå