|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dickson L.E. Ч History of the Theory of Numbers, Volume ll: Diophantine Analysis |
|
|
 |
| ѕредметный указатель |
Chu Shih-chien 4
Chuquet, N. 350 (350Ч351 599)
ChТin Chiu-Shao 60
Ciamberlini, C. 418
Cipolla, M. 621
circle see УRationalФ
Circulating function 115 117 119 161
Circulator 119Ч121 159
Clasen, B.I. 53
Class number 550 741 745 755 763 767Ч768
Claude, R.P.L. 403 (404)
Clay, H. 437
Clebsch, A. (434)
Clere, E. 478
Clowes, T. 403
Coccos 456 (447)
Coeci rule 79Ч81 (see also УVirginsФ)
Cole, W. 600 (601)
Colebrooke, H.T. [41 166 191 346Ч347 350 522 595 599]
Collignon, Ed. 320 322 564
Collins, E. 682
Collins, I. 520
Collins, J. 173 (174)
Collins, M. 381 440 465 475 468 475Ч476)
Colonne 6
Colucci, A. 671
Combinations 114 124 128 132Ч133 144 154Ч155 163
Combinatory analysis 36 141 145 161Ч162
Complex number 95 97 119 121Ч122 125 162 166 170 201 231 234 237 239Ч242 247Ч249 264Ч266 274 283 287 289 296Ч297 315 371 373Ч374 376 389 397Ч398 411 431 548 572 594 620 678 684 692 716 725 740 757
Composite 12 15 28 229
composition 145 147 151 157
Composition into squares 205 305
Composition of two forms 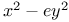 346Ч348 355 346Ч348 355
Concordant forma 472Ч477
Configuration 149 592
Congruence 19 33 87 406 673 678 684 687 692Ч693 700 758 761 766 771Ч772 775 УQuadraticФ)
Congruence, 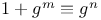 739 743 756 739 743 756
Congruence, 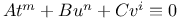 749 751 764 773Ч774 749 751 764 773Ч774
Congruence, 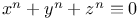 734 736 750 753 756Ч757 762Ч765 769 770 774 734 736 750 753 756Ч757 762Ч765 769 770 774
Congruent number 174 435 459Ч472 615
Congruent number of order n 472 701Ч703
Congruent to a sum, every number 86 87
Continuant 183 244 254 381
Continued fraction 19 21 32 47Ч49 51Ч54 68 72 75 93Ч94 99 149 182 198 219 233 237Ч238 240 242Ч244 250 267Ч268 295 344 350Ч353 355Ч358 361 364Ч365 367Ч372 374Ч401 408Ч412 417Ч418 473 540 587 641 673 686 762
Continued fraction, bracket notation in 49 149 240 357
Continued fraction, negative 379 381
Contravariant 431
Cook, A. 194
Cordier, H. 57
Cordone, G. 696
Corey, S.A. 302
Cornacchia, G. 673 762 765 736 762Ч763 765)
Cossali, P. 166 261 367 451 464 515Ч516 482)
Costa Lobo, F.M. 708
Coste, L.M.P. 19
Cotes, R. (47)
Couturat, L. [617]
Covenant 120 133 161 568
Crelle, A.L. 50 51 56
Cremona transformation 85 320
Crocchi, L. 69 70
Crofton 32
Cross, C.C. 518
Crowell, E.B. 346
Crussol 539 711Ч712
Csorba, G. 153 161
cube 6 8 23 25 28 33 35 38 177Ч180 187 246 251Ч252 255Ч257 УEveryФ УNumbersФ УSumФ)
Cube of sum of n numbers plus any one a cube 607Ч612
Cube, not a sum of 2 cubes 545Ч550
Cubes, equal sums of 550Ч562
Cubes, relations between 562Ч566 613
Cubic equation 220 545Ч613 661
Cubic form, binary 530 575 662
Cubic form, binary, made a cube 566Ч569
Cubic form, binary, made a square 569Ч572 640
Cubic form, ternary 588Ч595 695
Cubic function made square 457
Cubic residues 575
Cullen, J. 64
Cunliffe, J. 173 193 201 204 210Ч211 219 221 319 436 451Ч452 465 479 491 493 499 505Ч506 508 510Ч511 521 525Ч528 595 600 604 666 669 212 598)
Cunningham, A. 32Ч34 173 178 186 188 241 252 392 394Ч398 400 406 412 426 436 439 440 457Ч458 470Ч471 489 537 539 542 577 587 595 597 627 634 638 646 653Ч654 656 659 664Ч665 671 696Ч699 702 706 729 763 257 358 366 368 377 389 435 635 707)
Curjel, H.W. 30 601 751 755
Curtius, S. 191 (195)
Curtze, M. 59 342
Cuttaca 42 58
Cyclic method 63 346Ч348 349
Cyclotomy 243 251 295 370Ч372 376 398 736 750 753Ч754 763 765 769 770
Da Motta Pegado, L.P. 404
Dainelli, U. 266 (267)
Daniels, M.F. 57 64 145
Darboux, G. 219
Darling, H.B.C. 163
Dase, Z. 717
Davey, J. 180 193 212 601
David, E.A.A. 133
Davis, A. [62]
Davis, E.W. 62
Davis, R. 611 (726)
Davis, R.F. 273 299 501 513 537 571 572 606 702
De Billy, J. 173 175 177Ч178 185 445 482 509 519 566 569 602 618)
De Comberousse, C. 53 72 418 181
De Farkas, A. 684 709
De Gyergyoszentmiklos, D. 90
De Helguero, F. 581
De Joncourt, E. (587)
De Joncourt, Elie 12
De Jong, L. 700
De Jonquieres 168 (172)
De Jonquieres, E. 85 386 391Ч392 418 488 534 536 596 751 757 477 488 535 539 733 753 759)
De Khanikof, N. 379
De la Bottiere 46 61
De la Roche, E. 78 350
De la Vallee Poussin, C.J. 406
de la Vallee Poussin, Ch. 390
De Lagny, T.F. 46 61 71 80 167 206 447 639 189)
De Longchamps, G. 188 251 426 433 532 537 544
De lТHopital 354
De Montferrier 127
de Montmort, P.R. 9
De Morgan, A. 115 (117 126 135 145 151 160)
De Muris, J. 5
De Murr, C.T. [60 78 259 276 435]
De Ortega, J. 350
De Paoli, G. 55 (71)
De Paolis, R. 320
De Polignac, C. 66 168 392 753
De Rocquigny 270
De Rocquigny, G. 28 29 31 37 39 64 571 681 683 725
De Romilly, P.W. 757
De Sluse, R.F. 79
De Sluse, Rene F. 8 9 361 514
De Tannenberg, W. 274
De Tilly 751
De Virieu, J. 214 384
Decomposition into maximum powers 686
Decomposition into maximum squares 309 310
Decomposition into maximum triangular numbers 32
Dedekind, R. 371 378 399 742)
Definite polynomial 720 722 723Ч724
Degel, O. 434 542
Degen, C.F. 368 474 377 388Ч389 394Ч395 398Ч399 400)
Deidier, Abbe 10
Delambre, J.B.J. 714 (715Ч716) [343]
Delannoy, H. 314 536 576
Delaunay, B. 578
Delorme, H. 701
Deltour, A. 254 339
Dembschick, H. 53
Demme, C. 342
Denjoy, A. 96
| Denumerant 123 134Ч135
Deprez, J. 439
Derbes, J. 124
Derivatives of Arbogast 120 129 133 168
Desboves, A. 269 289 405 428 432 470 538 562 566Ч567 571 575 591 631Ч633 637 642 646 648 663 684 691 701 749 577 593 613 631Ч632 639 646)
Descartes, R. 6 7 175Ч176 201 228 259 260 275Ч276 402 536)
Descent, indefinite 228 256 275 353 466 533 546 548 550 574 576 616Ч619 632 634 636Ч638 738 748
Desmarest, E. 417 (402)
Despujols 703
Destournelles, G. Le Secq. 467
Determinant 75 76 82Ч84 89Ч93 95 121 125 244 291 314 410 556 594 679 689 695 741Ч742 756
Di San Robert, P. 694
Diagonal number 342
Diametral number 167 170
Dickson, L.E. 169 252 254 300 303 323 327 553 613 615 762Ч763 775 325 735Ч736 764Ч767 774Ч775)
Didon, F. 380
Dieu, T. 53
Difference of 2 squares 402Ч405 420 426 535 549
Difference of 2 squares, biquadrates not a square 615Ч620
Differences of cubes 535 549 578Ч581 607 662
Differences of order n 13 14 15 117 124 231Ч232 366
Differences of three squares 446 450 452 454 506
Differences of two biquadrates, product of two, a square 505
Differences of two biquadrates, product of two, equal to third 470
Differential operator 134 154 162
DIGITS 20 27 33 38 52 138 166 309 310 379 459 685 699
Dilling, A. 22
Diophantus 3 8 77 80 165Ч166 172 174Ч177 186 188 225Ч226 259 261 275 345Ч346 402 404 419 435 443 459 472 478 483 515Ч517 518 522 524Ч525 527 533 550 599 602 607 657 667 6Ч7 9 16 36 79 167 173Ч174 179 181Ч182 191Ч192 205Ч206 227 229 231 236Ч237 276 346 363 444Ч446 448 453Ч454 458 459 465 472 476 482Ч483 500 509 514 516 518Ч519 521Ч522 524 545 551 605 607Ч609 610Ч612 615Ч616 620 657Ч658 731)
Dirichlet, G.L. 51 94 236 242 263 290 337 369 370Ч373 376Ч377 405 409 423 540 574 593 677Ч678 735Ч736 738 741 233 235 240 248Ч249 264 296 302 333 365 367 876 378 381 393 396 398 412 426 578 691 735 738 760 771 775)
Discordant forms 473
Discriminant of cubic 548 595 662 736
Discriminant, equal unity 695Ч696
Distributions 146 162Ч163
Divisor product 701
Divisor with odd conjugate 130
Divulsions 101
Dixon, A.L. 763
Do Longchamps, G. 385
Dodecahedral 16 23
Dolgusin, P. 212
Domingues, A. 64
Dorn, W. 53
Dostor, G. 64 320 657 322)
Double equalities 80 443 445
Drach, S.M. 738
Draughon, H.W. 530
Drummond, J.H. 184 477 480 526
Du Hays 182 189 374
Dubouis, E. 302 316 398 769
Ducci, E. 53
Dujardin 416 689
Dupuis, J. [342]
Dupuy, M. 751
Durfee, W.P. 136 385
Dutenz, L. [699]
Dutordoir, H. 615 756
DТAndrea, C. 372
DТAvillez, J.F. 270
dТOcagne, M. 86 154 310 541
DТOvidio, E. 83
Eamonson, L. 148
Edaljii, J. 703
Eells, W.C. 274
Egen, P.N.C. 53 369
Egidi P.G. 169 190
Eisenstein, G. 236 263 287 305 374 594 662 234 239 241 306Ч308 312 314Ч316 431 695)
El-Hassar 350 (351)
Elefanti, F. 563
Elementary divisor 83 90
Elliott, E.B. 76
Elliott, R. 684
Elliptic function 25 113 146 209 220 224 235 246Ч247 249 250 262 265 285 293 295Ч296 301 305 309 310 315Ч318 333 378 389 411 457 482 501 569 572 640Ч641 644
Elliptic integral 482 641
Elliptic parameter 592Ч593
Elowson, G. 53
Elphinstone, M. [346]
Ely, G.S. 136 141
Emerson, W. 47 478 483 554
Emmerich, A. 32 456
Enestroem, G. 354
Engelhard, N. 12
Engler, E.A. 35
Ens, C. 60
Epicycloid 254
Epstein, P. 395
Equation 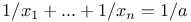 688Ч691 688Ч691
Equation 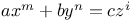 698 737Ч738 749 754Ч755 757Ч759 761Ч762 764 766 769 771Ч776 698 737Ч738 749 754Ч755 757Ч759 761Ч762 764 766 769 771Ч776
Equation 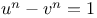 731 738 744 747 752Ч755 766 731 738 744 747 752Ч755 766
Equation 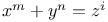 with x, y, z polynomials 760 774Ч775 with x, y, z polynomials 760 774Ч775
Equation 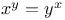 687 687
Equation linear in 1 unknown 401 690Ч691 700
Equation quadratic in x and in y 474 625 639Ч642
Equation with like first n coefficients 714Ч716
Equation with polynomial coefficients 695 743
Equivalent 91 96 677
Ermakov, V.P. 760
Escott, E.B. 33 37 184 271 393Ч394 397 480 487 498 536Ч538 542 561 571 585 597Ч598 606 633 658 681 683 697Ч698 706Ч709 710Ч711 715Ч716 534Ч537 541Ч542)
Euclid 165 (740 756)
EuclidТs g.c.d. process 45Ч49 52 53 61 93 95 352
Eugenio, V. 242 (251)
Euler, J.A. 12 261 546 669 717 717 719 724)
Euler, L. 10Ч17 46Ч48 61 71 80 101Ч106 167 173 175 179 193 202Ч204 221 229Ч232 260Ч261 276Ч279 281Ч282 354Ч358 362Ч364 401 404 407Ч408 412 414Ч415 421 435 448Ч449 450 464 472Ч474 478 481 497Ч498 502Ч503 505 507 509 514 517Ч519 520 522Ч524 526 530 533Ч534 539 540 545Ч546 552Ч554 567 569 570 572 578Ч579 582 599 608 618 621 622 624Ч625 627Ч628 634Ч635 639 640 644Ч645 648Ч649 660Ч661 668Ч668 682 684 687 692 705 732 862Ч864 22 25 27 35Ч37 39 48Ч51 53 58 61 63 75 103 112Ч113 115Ч118 120 123Ч124 126Ч128 130 133 136Ч138 140 146Ч147 149 155Ч156 159 162 171 185 201 204Ч205 207Ч208 219 221 223Ч224 225 229 232Ч234 239 240 243 244 250 256Ч257 265Ч266 270 279 281Ч282 284 286 291 297Ч300 309 318 341 343 362 364 361Ч362 367Ч369 373 374 378 381 385 392 394Ч395 400 404 408 418Ч419 421 428 430Ч431 440 446Ч447 454 456Ч458 464Ч465 468 471Ч472 474 476 478 493 499 500Ч501 503Ч506 511 518 521 525 531Ч532 547Ч549 550 554 559 560Ч561 569 572Ч574 579 580Ч585 597 599 618Ч619 620Ч621 623 626 629 632 635Ч638 641Ч642 646Ч648 652 660 663 669 671 681 684 696 700 716 729 732 738 753 759 764 766)
Evans, A.B. 181Ч182 187 197 215 219 380 384 437 491 513 515 526 561 584 605 611 666 680 701
Every number a sum of certain numbers 14 22Ч25 30 144 160 429 717 719 УCongruentФ УFigurateФ УGeometricalФ УPolygonalФ УPyramidalФ УSum УTriangularФ УWaringФ)
Every number a sum of four positive rational cubes 727Ч729
Every number a sum of nine cubes 23 717Ч725
Every number a sum of three rational cubes 726Ч727
Every number represented by  728 728
Every number represented by 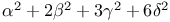 263 270 263 270
Every odd number represented 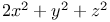 260 264 260 264
Exceptional prime 741
Faa di Bruno, F. 130 (120)
Faber Stapulensis 5 350
Fabre, F. 761
Fabry, E. 764
Factorial 8 124 126 143 232 679Ч682 722
Factoring 395Ч397 763
Factors of 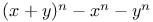 737Ч738 745Ч748 751Ч755 760Ч761 737Ч738 745Ч748 751Ч755 760Ч761
Farey numbers 149
Farey, J. (149)
Farquhar, C. 525
Faulhaber, J. 5
Fauquembergue, E 25 28 36 57 179 186 246 268 483 510 535Ч536 538 561Ч562 566 572 580Ч581 622 634 638 646Ч647 650 655 662 664 671 694 696 699 729 543 657)
Faure, H. 264 509 679
Favaro, J. 532
Fekete, M. 89
Feldhoff 212
Feliciano, F. 463 509
Fergola, E. 124Ч125 295 338
Fermat, P. 6Ч8 172Ч173 175Ч178 182 184Ч187 227Ч228 259 275Ч276 280 351 353 404 435 440 445 464 482 485 487 516Ч519 524 533 545 551 566 568Ч569 572 602 607 615Ч617 620Ч621 639 667 687 731 11 13 14 17 18 29 30 32 33 55 56 172 179 181 183Ч184 229 230 240 256 261 265 282 309 341 447 457 465 469 509 534 536 538 552 561 567 572 575 583 603 608 617 621Ч624 627 631Ч632 634 643 647 657)
Fermat, S. [172 191 227 731]
FermatТs last theorem 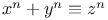 731Ч775 (see also УAlgebraicФ УBernouillianФ УClassФ УCongruenceФ УEquationФ УFactorsФ УPolynomialФ УRegularФ) 731Ч775 (see also УAlgebraicФ УBernouillianФ УClassФ УCongruenceФ УEquationФ УFactorsФ УPolynomialФ УRegularФ)
FermatТs last theorem 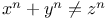 , criterion of Kummer 744 761 765 767 775 , criterion of Kummer 744 761 765 767 775
FermatТs last theorem 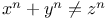 , criterion of Mirimanoff 761 768Ч769 771 , criterion of Mirimanoff 761 768Ч769 771
FermatТs last theorem 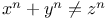 , criterion of Wieferich 764 766Ч768 771 775Ч776 , criterion of Wieferich 764 766Ч768 771 775Ч776
FermatТs last theorem 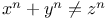 , n even 736Ч737 754Ч755 765 772Ч773 , n even 736Ч737 754Ч755 765 772Ч773
FermatТs last theorem 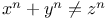 , n fractional 738 756 774 , n fractional 738 756 774
FermatТs last theorem 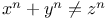 , n=10 772 , n=10 772
FermatТs last theorem 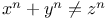 , n=11 774 , n=11 774
FermatТs last theorem 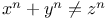 , n=14 736 , n=14 736
FermatТs last theorem 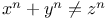 , n=3 545Ч550 767 , n=3 545Ч550 767
FermatТs last theorem 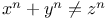 , n=37 745 755Ч756 769 , n=37 745 755Ч756 769
FermatТs last theorem 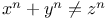 , n=4 615Ч620 757 701 , n=4 615Ч620 757 701
FermatТs last theorem 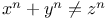 , n=5 732Ч733 735 738 755 760Ч761 771 773 , n=5 732Ч733 735 738 755 760Ч761 771 773
FermatТs last theorem 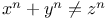 , n=59, n=67 745 , n=59, n=67 745
FermatТs last theorem 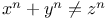 , n=6 732 758 772Ч773 776 , n=6 732 758 772Ч773 776
FermatТs last theorem 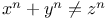 , n=7 663 737 739 746Ч748 761 , n=7 663 737 739 746Ч748 761
FermatТs last theorem 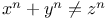 , x, y, z polynomials 749 750 757 760 770Ч771 774 775 , x, y, z polynomials 749 750 757 760 770Ч771 774 775
FermatТs theorem 55 171 238 251 281
Ferrari, F. 254Ч255 397 427 434 440 501 543 588 646 654 764
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



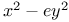
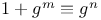
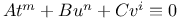
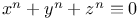
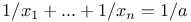
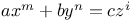
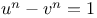
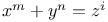 with x, y, z polynomials
with x, y, z polynomials 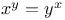

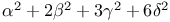
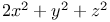
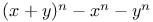
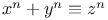
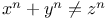 , criterion of Kummer
, criterion of Kummer