Авторизация
Поиск по указателям
Hogben L. — Handbook of Linear Algebra
Обсудите книгу на научном форуме Нашли опечатку?
Название: Handbook of Linear AlgebraАвтор: Hogben L. Аннотация: The Handbook of Linear Algebra provides comprehensive coverage of linear algebra concepts, applications, and computational software packages in an easy-to-use handbook format. The esteemed international contributors guide you from the very elementary aspects of the subject to the frontiers of current research. The book features an accessible layout of parts, chapters, and sections, with each section containing definition, fact, and example segments. The five main parts of the book encompass the fundamentals of linear algebra, combinatorial and numerical linear algebra, applications of linear algebra to various mathematical and nonmathematical disciplines, and software packages for linear algebra computations. Within each section, the facts (or theorems) are presented in a list format and include references for each fact to encourage further reading, while the examples illustrate both the definitions and the facts. Linearization often enables difficult problems to be estimated by more manageable linear ones, making the Handbook of Linear Algebra essential reading for professionals who deal with an assortment of mathematical problems.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2006Количество страниц: 1400Добавлена в каталог: 30.06.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Nondefective matrices 4—6 Nondegenerate properties, bilinear forms 12—2 Nondegenerate properties, sesquilinear forms 12—6 Nonderogatory matrices 4—6 Nondifferentiation 18—3 Nonempty sets, row and column indices 1—4 Nonhomogenous products 9—22 Nonlinear preservers 22—7 to 22—8 Nonnegative IEPs (NIEPs), fundamentals 20—5 Nonnegative IEPs (NIEPs), merging results 20—8 Nonnegative IEPs (NIEPs), nonzero spectra 20—7 to 20—8 Nonnegative IEPs (NIEPs), spectra 20—6 to 20—7 Nonnegative IEPs (NIEPs), sufficient conditions 20—8 to 20—10 Nonnegatives, constraints 50—3 Nonnegatives, factorization 9—22 Nonnegatives, fundamentals 9—1 Nonnegatives, integer rank 30—8 Nonnegatives, matrices, fundamentals 9—1 to 9—2 Nonnegatives, matrices, inequalities 17—11 Nonnegatives, matrices, inverse eigenvalue problem 9—22 Nonnegatives, matrices, irreducible matrices 9—2 to 9—7 Nonnegatives, matrices, max algebra 9—23 Nonnegatives, matrices, nonhomogenous products 9—22 Nonnegatives, matrices, nonnegative factorization 9—22 Nonnegatives, matrices, P-, 35—17 to 35—18 Nonnegatives, matrices, permanents 31—7 Nonnegatives, matrices, Perron — Frobenius theorem 26—2 Nonnegatives, matrices, product form 9—23 Nonnegatives, matrices, reducible matrices 9—7 to 9—15 Nonnegatives, matrices, scaling 9—20 to 9—23 Nonnegatives, matrices, sets 9—23 Nonnegatives, matrix factorization 63—5 to 63—8 Nonnegatives, sign pattern matrices 33—12 Nonnegatives, stable matrices 9—17 Nonnegatives, vectors 26—2 Nonnormality constant 44—10 Nonprimary matrix function 11—2 Nonrandom matrices 52—3 Nonrandom vectors 52—3 Nonregular matrices 32—7 to 32—9 Nonscalar multiplications, approximation algorithms 47—6 Nonscalar multiplications, fast algorithms 47—2 Nonseparability 35—2 Nonsingular properties, distribution 53—8 Nonsingular properties, fundamentals 2—9 to 2—10 Nonsingular properties, isomorphism 3—7 to 3—8 Nonsingular properties, matrices 1—12 Nonsingular properties, multivariate normal distribution 53—3 Nonsquare case 32—2 to 32—12 Nonsymmetric eigenproblems 75—17 to 75—20 Nonsymmetric eigenvalue problems 75—11 to 75—13 Nonsymmetric Lanczos process, Arnoldi process 49—10 Nonsymmetric Lanczos process, large-scale matrixcomputations 49—8 to 49—10 Nonsymmetric Lanczos process, linear dynamical systems 49—15 Nonsymmetric problems, ARPACK 76—8 Nonzero spectra 20—7 to 20—8 norm command, Matlab software 71—17 Norm estimation 18—9 to 18—10 Norm, Maple software 72—3 72—5 Norm, Mathematica software, fundamentals 73—26 73—27 Norm, Mathematica software, matrix algebra 73—10 73—11 Norm, Mathematica software, vectors 73—3 73—5 Normal equations, least squares problems 5—14 Normal equations, linear statistical models 52—8 Normal vector, Euclidean point space 66—2 Normal, Mathematica software 73—6 73—8 Normalization 23—5 Normalized properties, floating point numbers 37—11 Normalized properties, immanant 31—13 Normalized properties, matrices 25—6 Normalized properties, scaling nonnegative matrices 9—20 Norms, matrices 37—4 to 37—6 Not invertible 1—12 see Notation index N—1 to N—9 Notebooks, Mathematica software 73—1 Nth-derived algebra 70—3 null command, Matlab software 71—8 71—17 Null graphs 28—2 Null recurrent state 54—7 to 54—9 Null spaces, dimension theorem 2—6 to 2—9 Null spaces, kernel and range 3—5 Null spaces, linear independence, span, and bases 2—6 Null spaces, matrix range 2—6 to 2—9 Null spaces, rank 2—6 to 2—9 Nullity, linear independence, span, and bases 2—6 Nullity, matrix equalities and inequalities 14—12 to 14—15 NullSpace, Maple software, matrix factoring 72—9 NullSpace, Maple software, modular arithmetic 72—14 to 72—15 NullSpace, Mathematica software, fundamentals 73—27 NullSpace, Mathematica software, matrix algebra 73—10 73—12 Nullspaces 39—4 Numerical linear algebra, Maple software 72—13 to 72—15 Numerical linear algebra, support routines 77—1 Numerical methods, affine parameterized IEPs 20—11 to 20—12 Numerical methods, fast matrix multiplication 47—1 to 47—10 Numerical methods, high relative accuracy computation 46—1 to 46—16 Numerical methods, implicitly restarted Arnoldi method 44—1 to 44—12 Numerical methods, iterative solution methods 41—1 to 41—17 Numerical methods, large-scale matrixcomputations 49—1 to 49—15 Numerical methods, linear systems, direct solutions 38—1 to 38—17 Numerical methods, linear systems, efficiency 37—1 to 37—21 Numerical methods, linear systems, error analysis 37—1 to 37—21 Numerical methods, linear systems, factorizations 38—1 to 38—17 Numerical methods, linear systems, least squares solutions 39—1 to 39—12 Numerical methods, linear systems, matrix norms 37—1 to 37—21 Numerical methods, linear systems, sparse matrix methods 40—1 to 40—18 Numerical methods, linear systems, stability 37—1 to 37—21 Numerical methods, linear systems, vector norms 37—1 to 37—21 Numerical methods, Markov chains 54—12 to 54—14 Numerical methods, singular value decomposition 45—1 to 45—12 Numerical methods, stability and instability 37—18 to 37—21 Numerical methods, structured matrix computations 48—1 to 48—9 Numerical methods, symmetric matrix techniques 42—1 to 42—22 Numerical methods, unsymmetric matrix techniques 43—1 to 43—11 Numerical orthogonality 46—2 Numerical radius 18—1 Numerical range, boundary points 18—3 to 18—4 Numerical range, dilations 18—9 to 18—10 Numerical range, examples 18—1 to 18—3 Numerical range, fundamentals 18—1 Numerical range, location 18—4 to 18—6 Numerical range, matrix mappings 18—11 Numerical range, matrix products 18—8 to 18—9 Numerical range, norm estimation 18—9 to 18—10 Numerical range, properties 18—1 to 18—3 Numerical range, radius 18—6 to 18—8 Numerical range, special boundary points 18—3 to 18—4 Numerical range, spectrum 18—3 to 18—4 Numerical range, unitary similarity 7—2 Numerical rank 39—11 Numerical stability and instability, error analysis 37—18 to 37—21 Numerical stability and instability, Strassen’s algorithm 47—4 Numerically orthogonal matrices 46—2 numnull command, Matlab software 71—13 O and o P—5 Objective function 50—1 Oblique Petrov — Galerkin projection, eigenvalue Oblique Petrov — Galerkin projection, computations 49—12 Oblique Petrov — Galerkin projection, large-scale matrix computations 49—2 Observability Hessenberg form 57—9 Observability Kalman decomposition 57—7 Observability matrix 57—7 Observableness, control theory 57—2 Observer equation 57—2 Octonions, generalized 69—4 Odd cycle 33—2 Oettli — Prager theorem 38—3 Off-diagonal entry 1—4 Off-norm, Jacobi method 42—17 One(1)-chordal graphs 35—2 One(1)-norm 37—2 One-bit quantum gate 62—2 One-dimensional harmonic oscillator 59—8 One-sided Jacobi SVD algorithm, high relative accuracy 46—2 to 46—5 One-sided Jacobi SVD algorithm, positive definite matrices 46—11 One-sided Jacobi SVD algorithm, preconditioned Jacobi SVD algorithm 46—6 One-sided Jacobi SVD algorithm, singular value decomposition 45—5 One-sided Jacobi SVD algorithm, symmetric indefinite matrices 46—15 One-to-one, kernel and range 3—5 Onto, kernel and range 3—5 Open halfspaces 66—2 Open sector 33—14 Operations and functions, Maple software 72—3 72—5 Operator norms, matrix norms 37—4 Operator norms, unitary similarity 7—2 Optimal control problem 57—14 Optimal estimation problem 57—12 Optimal Krylov space methods 41—4 to 41—11 Optimal pivoting strategy 42—17 Optimal solution 50—1 Optimal value 50—1 Optimality conditions 51—5 to 51—7 Optimality theorem 51—6 Optimization, linear programming 50—1 50—1 Optimization, matrix games 50—18 Optimization, semidefinite programming 51—1 to 51—11 Optimization, standard row tableaux 50—8 Orbit, linear dynamical systems 56—5 Orbit, simultaneous similarity 24—8 Order predictable signals 64—7 Order sequence 58—8 Order, control theory 57—2 Order, graphs 28—1 Order, reducible matrices 26—9 Ordinary least squares estimator 52—8 Ordinary least squares solution 52—8 Orientation 13—24 to 13—26 Orientation preservation 56—5 Oriented incidence matrix 28—7 orth command, Matlab software 71—17 Orthogonal Petrov — Galerkin projection, Arnoldi process 49—10 Orthogonal Petrov — Galerkin projection, large-scale matrix computations 49—2 Orthogonal Petrov — Galerkin projection, symmetric Lanczos process 49—7 Orthogonal properties, classical groups 67—5 Orthogonal properties, complement 5—3 Orthogonal properties, congruence 25—10 Orthogonal properties, Euclidean point space 66—2 Orthogonal properties, Euclidean spaces 65—4 Orthogonal properties, fundamentals 5—3 to 5—5 Orthogonal properties, general properties 69—5 Orthogonal properties, least squares solutions 39—5 to 39—6 Orthogonal properties, linear inequalities and projections 25—10 Orthogonal properties, projection 5—6 to 5—8 Orthogonal properties, rank revealing decomposition 39—11 Orthogonal properties, sign-pattern matrices 33—16 to 33—17 Orthogonal properties, symmetric bilinear forms 12—3 Orthogonal properties, symmetric indefinite matrices 46—14 Orthogonal properties, symmetric matrix eigenvalue techniques 42—2 Orthogonal properties, unitary similarity 7—1 Orthogonality relations 68—6 to 68—8 Orthogonalization 38—13 to 38—15 Oscillation modes 59—2 to 59—5 Oscillatory matrices 21—2 Oseledets theorem 56—14 to 56—15 Ostrowski theorem, eigenvalue problems 15—13 Ostrowski theorem, spectrum localization 14—6 to 14—7 Outer normal, Euclidean simplexes 66—7 Outer, Mathematica software 73—2 73—3 73—4 Outerplanar graphs 28—4 OuterProductMatrix, Maple software 72—3 Outlets 66—13 Output Feedback 57—7 57—13 Output space 57—2 Output vector 57—2 Output, algorithms and efficiency 37—16 Output, LTI systems 57—14 Ovals of Cassini 14—6 to 14—7 Overall constraint length 61—12 Overflow, floating point numbers 37—12 P-, 35—15 to 35—17 P-, 19—3 p-Lie algebra 70—2 p-Norm 37—2 Packed format 74—2 Pade approximate 11—10 to 11—11 11—12 Pade iterations 11—12 Pade models, dimension reduction 49—14 Pade models, linear dynamical systems 49—15 PadRight, Mathematica software 73—13 Page repository 63—9 Page, Larry 54—4 63—9 63—10 PageRank, fundamentals 63—10 PageRank, information retrieval 63—10 to 63—14 PageRank, Markov chains 54—4 to 54—5 PageRank, vector 63—11 PageRank, Web search 63—9 Pairwise orthogonality 7—5 Paley — Wiener theorem 64—3 to 64—4 Pan, V. 47—7 Pappus’ theorem 65—8 65—9 Parabolic subgroup 67—4 Parabolic subgroup, BN structure 67—5 Parallel hyperplanes 66—2 Parallel vector subspace 65—2 Parallelepiped, Gram matrices 66—5 Parallelogram law, inner product spaces 5—3 Parallelogram, Gram matrices 66—5 Parameters, graphs 28—9 to 28—11 Parametric programming 50—17 to 50—18 Parametrization ofcorrelation matrices 8—8 Parity check, matrix 61—3 Parity check, polynomial 61—7 Parlett and Reinsch studies 43—3 Parlett’s recurrence 11—10 11—11 Parseval’s Inequality 5—4 Parter vertices 34—2 to 34—4 Parter — Wiener theorem, given multiplicities 34—9 Parter — Wiener theorem, multiplicities and Parter vertices 34—2 Parter — Wiener vertex 34—2 Partial 35—12 to 35—13 Partial completely positive matrices 35—10 Partial copositive matrices 35—11 Partial correlarandom vectors 52—4 Partial correlation coefficient, linear prediction 64—8 Partial correlation matrix 52—4 Partial covariance matrix 52—4 Partial differential equations 58—7 Partial doubly nonnegative matrices 35—10 Partial entry sign symmetric P-, 35—19 to 35—20 Partial entry weakly sign symmetric P-, 35—19 to 35—20 Partial Euclidean distance matrices 35—10 Partial inverse M-matrices 35—14 Partial M-matrices 35—12 to 35—13 Partial matrices 35—2 Partial matrix multiplication 47—8 Partial nonnegative P-, 35—17 to 35—18 Partial order, checkerboard 21—9 Partial P-, 35—15 Partial pivoting 40—18 see Partial positive definite matrices 35—8 Partial positive P-matrices 35—17 Partial positive semidefinite matrices 35—8 Partial Schur decomposition 44—6 44—8 Partial semidefinite ordering, positive definite matrices 8—10 Partial semidefinite ordering, random vectors 52—4 Partial strictly copositive matrices 35—11 Partition, Mathematica software 73—14 Partitioned matrices, block diagonal matrices 10—4 to 10—6 Partitioned matrices, block matrices 10—1 to 10—3 Partitioned matrices, block triangular matrices 10—4 to 10—6 Partitioned matrices, Kronecker products 10—8 to 10—9
Реклама
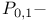and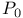 
-matrices, completion problems 
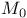-matrices 
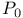-matrices 
|
|
О проекте