|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rockafellar R.T. Ч Convex analysis |
|
|
 |
| ѕредметный указатель |
Abnormal program 318
Addition of convex cones 22
Addition of convex functions 33 77 145 176 179Ч180 223 263
Addition of convex processes 415 421
Addition of convex sets 16Ч17 49 74Ч75 146 175 183
Addition of epigraphs 34
Addition of saddle-functions 402
Adjoint of a bifunction 309Ч326 330 353Ч358 401Ч412
Adjoint of a convex process 417ff
Adjoint of a linear transformation 3 9 310
aff see УAffine hullФ
Affine functions 23 25 27 102Ч103
Affine functions, partial 70 107 431
Affine hull 6 45 154
Affine hull of convex cone 15
Affine hull, characterization 113
Affine independence 6Ч7 154
Affine sets 3Ч9
Affine sets, closed halves 165Ч166
Affine sets, representation 4Ч8
Affine transformations 7Ч8 44Ч45
Alternative system of inequalities 201
Asymptotic cone 61
Ball 43
Barrier cone 15 113 123
Barycenter 12
Barycentric coordinates 7
Bi-affine functions 302
Bifunction 291ff (see also УConvex bi-functionsФ)
Bilinear functions 351Ч352 411
Boundedness conditions 54 64 68Ч69 88 123
CaratheodoryТs theorem 153Ч157 427
Chemical equilibrium problem 430
Circulations 204 208 272 337Ч338
Cl see УClosureФ
Closed bifunction 293
Closed concave function 308
Closed convex function 52 (see also УClosureФ)
Closed saddle-function 363 (see also УClosureФ)
Closure of a bifunction 293 305Ч306 310 403 407
Closure of a concave function 307Ч308
Closure of a convex function 51Ч59 72Ч81 102Ч104 218Ч219 425
Closure of a convex process 415
Closure of a convex set 43Ч50 72Ч81 112 421Ч422
Closure of a saddle-function 359Ч369 390
Closure of an epigraph 52
Co-finite 116 259Ч260 411Ч412
Complete non-decreasing curves 232 338 428
Composition of a convex function and a linear transformation 38 78
Composition of convex functions 32
Composition of convex processes 416 422Ч423
Concave bifunctions 308ff
Concave closure of a saddle-function 350Ч353
Concave functions 25 307Ч308 426
Concave functions, monotone conjugates 110
Concave programs 308ff
Concave-convex functions 349ff
Cone 13
Conjugacy correspondence 104 123Ч124
Conjugacy correspondence for saddle-functions 389ff
Conjugate concave functions 111 308
Conjugate convex functions 104Ч111 113Ч118 121Ч124 133Ч137 140Ч150 173 179Ч180 263Ч264 405 421 425Ч426
Conjugate convex functions, definition 104
Conjugate convex functions, subgradients 218
Conjugate saddle-functions 390Ч391 395 432
Consequence 199
Consistency 185 295 309 315
Constancy space 69
Continuity of convex functions 82Ч89 426
Continuity of derivatives 227Ч238
Continuity of gradient mappings 246 376Ч377
Continuity of saddle-functions 370Ч371
Continuity, joint 89
Continuity, uniform 86Ч87
Continuous extensions 85
conv see УConvex hullФ
Convergence of convex functions 90Ч91 426
Convergence of gradients 248Ч249
Convergence of saddle-functions 372 375Ч378
Convergence of subgradients 233Ч236
Convex bifunctions 293Ч306 309Ч311 350Ч358 384Ч389 401Ч412 417Ч418
Convex closure of a saddle-function 350Ч353
Convex combinations 11Ч12
Convex combinations of points and directions 154
Convex cones 13Ч15 22 50
Convex cones, generation 78 122 126 156 178
Convex cones, polar 121Ч125
Convex cones, polyhedral 170 178
Convex cones, separation 100Ч101
Convex function 23
Convex function, co-finite 259
Convex function, differential conditions for convexity 26Ч27
Convex function, finitely generated 172Ч173
Convex function, interpolation properties 25
Convex function, Legendre type 258
Convex function, partial quadratic 109 431
Convex function, polyhedral 172Ч177
Convex function, polynomial 268
Convex function, quadratic 27 108
Convex function, separable 270Ч271 285Ч290 337Ч338
Convex function, symmetric 109Ч110
Convex hull 12 177 427
Convex hull of a set of points and directions 153Ч155
Convex hull, of a bounded set 158
Convex hull, of a collection of convex functions 37 81 149 156
Convex hull, of a collection of convex sets 18 80 156Ч157
Convex hull, of a non-convex function 36 103 157Ч158
Convex hull, of two convex cones 22
Convex hull, relative interior 50
Convex processes 413Ч423 432
Convex processes, polyhedral 415
Convex programs, generalized 291Ч326 355Ч356 385Ч387
Convex programs, normal 316Ч319
Convex programs, ordinary 273Ч291 293Ч294 296 298 300 320Ч326 429
Convex programs, polyhedral 301Ч303
Convex set 10
Convex set as a cross-section of a cone 15
Convex set, finitely generated 170Ч171
Convex set, polyhedral 11
Convex set, symmetric 16
Convex-concave functions 349ff
Cyclically monotone mappings 238Ч240
Decomposition principle 285Ч290 312Ч313 429
Derivatives, directional 213Ч221 226 244Ч245 264 299Ч301 372Ч377
Derivatives, partial 241 244 376
Derivatives, right and left 214 216 227Ч232
Differentiability 241Ч246 428
Differentiability of saddle-functions 375Ч376
DIM see УDimensionФ
Dimension of a convex function 23 71
Dimension of a convex set 12Ч13 45Ч46 126
Dimension of an affine set 4
Direct sums 19 49
Directed graphs 204 208 272 337Ч338
Direction 60
Direction of affinity 70
Direction of constancy 69
Direction of linearity 65
Direction of recession 61 69 264Ч270
Directional derivatives 213Ч221 226 244Ч245 264 299Ч301 372Ч377
Distance function 28 34
Distributive inequalities 416
DOM see УEffective domainФ
Dual programs 310Ч338 355Ч356 429ff
Dual systems of inequalities 201
Effective domain of a bifunction 293
Effective domain of a concave function 307
Effective domain of a convex function 23 25 122
Effective domain of a convex process 413
Effective domain of a saddle-function 362 366 391Ч392
| Effective domain, relative interior 54
Eigensets 423
Elementary vectors 203Ч208 272 428
Epi see УEpigraphФ
Epigraph 23 307
Epigraph, closure 52
Epigraph, relative interior 54
Epigraph, support function of 119
Equi-Lipschitzian 87Ч88
Equicontinuity 88
Equilibrium prices 276Ч277 280 299Ч300
Equivalent saddle-functions 363Ч369 383 394
Essentially smooth function 251Ч258
Essentially strictly convex function 253Ч260
Euclidean metric 43
Exposed directions 163 168
Exposed faces 162Ч163
Exposed points 162Ч163 167Ч168 243 427
Exposed rays 163 169
Extensions of saddle-functions 349 358 363 366 369
Extreme directions 162Ч166 172
Extreme points 162Ч167 172 344Ч345 427
Extreme points at infinity 162
Extreme rays 162 167
Faces 162Ч165 171 427
Faces, exposed 162Ч163
FarkasТ lemma 200Ч201
Feasible solutions 274 295 308 315
FenchelТs Duality Theorem 327ft 408 430
FenchelТs inequality 105 218
Finitely generated convex function 172Ч173
Finitely generated convex set 170Ч171
Flat 3
flows 204 208 272 337Ч338
Fully closed saddle-function 356 365
Gale Ч Kuhn Ч Tucker Theorem 317 337 421 430Ч431
Gauge 28 35 79 124Ч125 128Ч131 427
Gauge-like functions 133
Generalized convex programs 291Ч326 355Ч356 385Ч387
Generalized polytope 171
Generalized simplex 154Ч155
Generators 170
Geometric mean 27 29
Geometric programming 324Ч326 430
Gradients 213 241Ч250 300 375Ч378 396
Graph domain 293
Graph function 292
Half-spaces 10 99 112 160
Half-spaces in 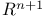 102 102
Half-spaces, homogeneous 101
Half-spaces, tangent 169
Half-spaces, upper 102
Half-spaces, vertical 102
HellyТs theorem 191Ч197 206 267 427Ч428
Hessian matrix 27
Hyperplanes 5
Hyperplanes, in 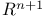 102 102
Hyperplanes, representation 5
Hyperplanes, supporting 100
Hyperplanes, tangent 169
Hyperplanes, vertical 102
Image of a convex function 38 75 142 175 255 405 409Ч412 416 421
Image of a convex set 19 48 73 143 174 414Ч415 421Ч422
Image-closed bifunction 352Ч353
Improper convex function 24 34 52Ч53
Improper saddle-function 366
Incidence matrix 204 208
Inconsistency 185 315
Indicator bifunction 292Ч293 310 355 417
Indicator function 28 33 425
Indicator function, conjugate 113Ч114
Inequalities 129Ч130 425 428
Inequalities, between functions 38 104
Inequalities, between vectors 13
Inequalities, consistent 185
Inequalities, convex 29 55 58 185Ч197
Inequalities, homogeneous 14
Inequalities, linear 10Ч11 13Ч14 62 65 113 122 170 185 198Ч209
Infimal convolution 34 38 76Ч77 145 175 179Ч181 254 425 427
Infimal convolution of bi-functions 401Ч404
Infimal convolution, partial 39
Inner product equation 355 409Ч412 419Ч421
Inner product of a vector and a function 350
Inner product of a vector and a set 417
Inner product of two functions 408Ч412
Inner product of two sets 422Ч423
Inner product of two vectors 3
int see УInteriorФ
Interior 43Ч44 47 112
Intersections of convex cones 13 22
Intersections of convex sets 10 64 145
Intersections, relative interiors 47
interval 202
Inverse addition 21
Inverse addition of epigraphs 40
Inverse bifunction 384Ч385 388Ч389 401 405Ч406
Inverse image of a convex function 38 78 141 225
Inverse image of a convex set 19 49 64 143 174
Inverse process 414 418
Kernel of a saddle-function 367Ч369
Kuhn Ч Tucker coefficients 274Ч277 280 429
Kuhn Ч Tucker conditions 282Ч284 304 333Ч338 386Ч387 429
Kuhn Ч Tucker theorem 283 387
Kuhn Ч Tucker vectors 274Ч290 295Ч306 309 387
Lagrange multipliers 273Ч274 280 283 429
Lagrangian function 280Ч290 296Ч298 302Ч305 309 314 385Ч387
Lattice of convex functions 38
Lattice of convex processes 416
Lattice of convex sets 18
Legendre conjugate 256Ч260
Legendre transformation 251 256 427 429
Level sets 28Ч29 55 58Ч59 70 123 127 222 263Ч265
Level sets of support functions 118
Line 3Ч4
Line segment 10 12
Lineality 65 126
Lineality of a convex function 70 117
Lineality space 65 70 117 126
Linear combinations, convex 11
Linear combinations, of convex functions 33;
Linear combinations, of convex sets 17Ч18
Linear combinations, positive and non-negative 14
Linear programs 301Ч302 311Ч312 317 332 334Ч335 337 425
Linear variety 3
Lipschitz conditions 116 237 370Ч371
Lipschitzian 86
Locally simplicial sets 84Ч85 184
Lower boundary 33
Lower closed saddle-function 365
Lower closure 357Ч359 368
Lower conjugate 389Ч391
Lower semi-continuity 51Ч52 72 77
Lower semi-continuous hu 1152 54
Lower simple extension 349 358
Maximum of a convex function 342Ч346
minimax 379 391Ч393 397Ч398 431
Minimum set 263Ч266
Minimum set of a convex function 263ff
Minkowski metric 132
Monotone conjugacy 111 426
Monotone mappings 240 340 396
Monotonicity 68Ч69 77 85Ч86
MoreauТs Theorem 338
Multiplication of bifunctions 409Ч412
Multiplication of convex processes 422Ч423
Network programming 272 337Ч338 431
Non-decreasing curves 232 338
Non-decreasing functions 68Ч69 77 85Ч86 232 338
Non-negative orthant 13 122 226
Norm 129Ч132 136 427
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте