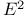|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| O'Neill B. — Elementary differential geometry |
|
|
 |
| Предметный указатель |
Minimal surface examples 238
Minimal surface of revolution 236—238
Minimal surface ruled 233(Ex. 22)
Minimal surface, fiat 263(Ex. 1)
Minimal surface, Gauss mapping 294(Ex. 6) 296(Ex.
Minimization of arc length 340
Mobius band 178 180(Ex.
Monge patch 127 219
Monkey saddle 132(Ex. 6) 205 231(Ex.
Monkey saddle, Gaussian curvature 220(Ex. 5)
n-polygon 388—389
Natural coordinate functions 4
Natural frame field 9
Neighborhood 43 125
Neighborhood, normal 341
Norm 43
Normal curvature 195—202 221(Ex.
Normal curvature, sign of 198
Normal section 197
Normal vector field 147
One-to-one 2
Onto 2
Open interval 15
Open set 5 43 151—152
Orientable surface 177—178 185(Ex.
Orientation of a frame 107
Orientation of a patch 285
Orientation of a paving 285
Orientation of a surface 195 284
Orientation of tangent frame fields 291
Orientation, determined by a patch 374
Orientation-preserving (-reversing) isometry 109 296
Orientation-preserving (-reversing) reparametrization 52
Oriented angle 291
Orthogonal coordinates 276—280
Orthogonal coordinates, Gaussian curvature formula 278
Orthogonal matrix 46
Orthogonal transformation 100
Orthogonal vectors 44
Orthonormal expansion 45—46 83
Orthonormal frame see "Frame"
Osculating circle 64(Ex. 6)
Osculating plane 61
Parallel curves 116
Parallel postulate 336
Parallel surfaces 209—210
Parallel translation 323
Parallel vector field 54—55 322
Parallel vectors 6
Parameter curves 133
Parametrization in a surface 135
Parametrization in a surface, criteria for regularity 136 140(Ex.
Parametrization in a surface, decomposable into patches 165(Ex. 9)
Parametrization of a curve 21
Partial velocities 134 136 146
Patch 124—137
Patch principal 220(Ex. 9) 280(Ex.
Patch, abstract 182 184
Patch, geometric computations 210—216
Patch, Monge 127
Patch, orthogonal 220(Ex. 9) 276—280
Patch, proper 124 152(Ex.
Patchlike 2-segment 281
Paving 283 377
Planar point 205
Plane in 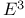 60 131(Ex. 228 256 60 131(Ex. 228 256
Plane in 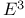 , identified with , identified with 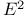 126 126
Poincare half-plane 309(Ex. 2)
Poincare half-plane, Gaussian curvature 317(Ex. 1)
Poincare half-plane, geodesies 337(Ex. 6)
Poincare half-plane, isometric to hyperbolic plane 371(Ex. 15)
Poincare half-plane, polar circles 351(Ex. 2)
Point of application 6
Pointwise principle 8
Polar circle 346 359—360
Polar disc 361(Ex. 2)
Polygonal region 386
Pre-geodesic 330
Principal curvatures 199—207
Principal curvatures as characteristic values 200
Principal curvatures, formula for 206
Principal curve 223—225 230—232 263(Ex.
Principal direction 199
Principal frame field 254
Principal normal 57 66 69
Principal vectors 199 220(Ex. 223(Ex.
Principal vectors as characteristic vectors 200
Projective plane 182—183
Projective plane, geodesies 337(Ex. 8)
Projective plane, geometric structure 317(Ex. 6)
Projective plane, homogeneity 371(Ex. 11)
Projective plane, natural mapping (projection) 183
Projective plane, topological properties 186(Ex. 2)
Pseudosphere see "Bugle surface"
Pullback 163
Quadratic approximation 202—204
Quadric surface 142 294(Ex.
Rectangular decomposition 377
Reflection 109
Regular curve 20
Regular mapping 38 161
Reparametrization 18
Reparametrization, monotone 56(Ex. 10)
Reparametrization, orientation-preserving (-reversing) 52
Reparametrization, unit-speed 51
Riemann 304 336
Riemannian geometry 308 389—390
Riemannian manifold 308
Rigid motion see "Isometry of Euclidean space"
Rigidity 301(Ex. 1)
Rotation 111(Ex. 4)
Ruled surface 140—143 227 231—233
Ruled surface, noncylindrical 232(Ex. 14)
Ruled surface, total Gaussian curvature 294(Ex. 9)
Ruling 140
Saddle surface 192
Saddle surface, doubly ruled 227
Saddle surface, Euclidean symmetries 303(Ex. 9)
Saddle surface, patch computations 214—216
Saddle surface, principal vectors 221(Ex. 11)
Scalar multiplication 3 8—9
Scale factor 268
Scherk's surface 222(Ex. 21)
Scherk's surface, Gauss mapping 296(Ex. 20)
Scherk's surface, patch in 303(Ex. 11)
Schwartz inequality 44
Serret 81
Shape operator 190—194
| Shape operator as derivative of Gauss mapping 289
Shape operator of an immersed surface 368
Shape operator, characteristic polynomial 208(Ex. 4)
Shape operator, covariant derivatives and 324(Ex. 3)
Shape operator, frame fields, in terms of 248
Shape operator, Gaussian and mean curvature, and 203
Shape operator, normal curvature and 196
Shape operator, preserved by Euclidean isometries 297—298
Shape operator, principal curvatures and vectors, and 200
Shape operator, proof of symmetry 212—213 251(Ex.
Shortest curve segment 340
Sign of an isometry 108
Simple region 294—295
Simply connected surface 176 363
Slant of a geodesic 331 338
Smooth overlap 145 182
Speed 51
Sphere 128
Sphere with handles 379
Sphere, conjugate points 354 357—358
Sphere, Euclidean symmetries 302(Ex. 8)
Sphere, frame-homogeneity 370(Ex. 6)
Sphere, Gaussian curvature 207 219(Ex. 253 360 361(Ex.
Sphere, geodesies 228—229 346—347
Sphere, geographical patch 134—135 277—278
Sphere, geometric characterizations 258 259 262
Sphere, geometric structures 383
Sphere, holonomy 323—324 337(Ex.
Sphere, local isometries 363—365
Sphere, rigidity 301(Ex. 1)
Sphere, shape operator 191—192
Sphere, topological properties 176—178 378
Spherical curve 63 65(Ex.
Spherical frame field 83
Spherical frame field, adapted to sphere 248—249 277—278
Spherical frame field, dual and connection forms 94—95
Spherical image of a curve 71 75(Ex.
Spherical image of a surface see "Gauss mapping"
Standard geometric surface 363—366
Stereographic plane 314
Stereographic projection 160 162
Stereographic projection as conformal mapping 271(Ex. 14)
Stereographic sphere 314 337(Ex.
Stokes' theorem 170—172 387(Ex.
Straight line 15 18 55 229(Ex.
Straight line, length-minimizing propertie 56(Ex. 1)
Striction curve 232(Ex. 14)
Structural equations on 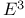 92—95 92—95
Structural equations on a surface 249 252 292 311—312
Subset 1
Support function 218 222 256
Surface in 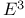 125 306 367 125 306 367
Surface in 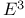 , implicit definition 127—128 , implicit definition 127—128
Surface of revolution 129—130 234—244
Surface of revolution, area 292(Ex. 2)
Surface of revolution, augmented 133(Ex. 12)
Surface of revolution, diffeomorphism types 187(Ex. 8)
Surface of revolution, Gaussian curvature 235 238 242 243(Ex.
Surface of revolution, geodesies 338(Ex. 13)
Surface of revolution, local characterization 270(Ex. 12)
Surface of revolution, meridians and parallels 130
Surface of revolution, natural frame field 279
Surface of revolution, of constant curvature 239—241 244(Ex. 294(Ex.
Surface of revolution, parametrization, canonical 238
Surface of revolution, parametrization, special 143(Ex. 13)
Surface of revolution, parametrization, usual 138—139
Surface of revolution, principal curvatures 235
Surface of revolution, principal curves 225 235
Surface, abstract 182—184
Surface, geometric 305
Surface, immersed 368
Surface, topological properties 182(Ex. 14)
Surface, total curvature 293(Ex. 5)
Symmetry equation 249
Tangent bundle 185
Tangent line 22(Ex. 9)
Tangent plane 146 150(Ex.
Tangent space 7
Tangent surface 231(Ex. 11)
Tangent surface, isometries of 270(Ex. 5) 301(Ex.
Tangent vector to 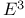 6 14 6 14
Tangent vector to a surface 146 183—184
Theorema egregium 273—275
Topological properties 176—182 380n
Toroidal frame field 84(Ex. 4) 2) 250—251
Torsion 58 66
Torsion formula 69
Torsion sign 114—115
Torus of revolution 139
Torus of revolution, Euler — Poincare characteristic 379 387(Ex.
Torus of revolution, Gauss mapping 194(Ex. 5) 290—291
Torus of revolution, Gaussian curvature 204—205 235—236
Torus of revolution, patch computations 235—236
Torus of revolution, total Gaussian curvature 287 291
Torus of revolution, usual parametrization 139
Total curvature of a curve 76(Ex. 16)
Total Gaussian curvature 286—291 380—385
Total Gaussian curvature of a patch 325(Ex. 5)
Total Gaussian curvature, Euler — Poincare characteristic, and 380
Total Gaussian curvature, Gauss mapping, and 290
Total Gaussian curvature, holonomy and 325(Ex. 5)
Total geodesic curvature 372—375 386(Ex. 389(Ex.
Transferred frame field 272—273
Translation 98—100 109
triangle 383—385
Triangle inequality 347
Triple scalar product 48—49 108
Tube 221(Ex. 16)
Umbilic point 200 221(Ex. see
Unit normal function 211 368
Unit normal vector field 180(Ex. 5) 190
Unit points 34
Unit speed curve 51
Unit sphere 125
Unit tangent 56 66 69
Unit vector 44
Vector see "Tangent vector"
Vector analysis 31(Ex. 8)
Vector field on a curve 52—54 320
Vector field on a surface in 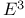 147—149 151(Ex. 147—149 151(Ex.
Vector field on a surface in 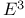 , normal 147 149 , normal 147 149
Vector field on a surface in 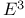 , tangent 147 149 , tangent 147 149
Vector field on an abstract surface 183
Vector field on Euclidean space 8
Vector part 6
Velocity 17—18 183—184
Vertices 373—374
Wedge product 27—28 153
Winding number 174(Ex. 5)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте