јвторизаци€
ѕоиск по указател€м
Ercolani N.M., Gabitov I.R., Levermore C.D. Ч Singular limits of dispersive waves
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Singular limits of dispersive wavesјвторы: Ercolani N.M., Gabitov I.R., Levermore C.D.јннотаци€: In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension. As a result, water with a free surface is generally considered to be a dispersive medium.
язык: –убрика: ‘изика /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 1994 оличество страниц: 369ƒобавлена в каталог: 16.02.2014ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
79 70 275 283 Abel hierarchy 84Ч87 Abel transform 78 80 107 177 Abelian differential 3 8 9 16 106Ч108 115 162 Abelian integral 108 109 288 action 166 173 216 241 274 278 305Ч306 311 Adams Ч Bashfort method 333Ч335 337 341 Adiabatic 105 113 216 274 Angle-representation 276 279 281 283Ч288 Asymptotic ansatz 113 114 179 Atomic measure 251Ч253 Attractor 39Ч40 52 Autocorrelation function 183Ч201 Averaged Whitham equation for Toda lattice 5Ч10 Backlund transformation 118 146 Baker vector/Baker function 121 122 Baker Ч Akhiezer function 9 79Ч82 109 112 118 120 177 Benney equations 53 55Ч59 61 65 143Ч155 168 170 Benney hierarchy 61Ч62 65 Bifurcation 39Ч40 48 305 306 309 311 Billiards 219Ч234 Binary oscillation 331Ч332; see Period-two oscillation Boltzmanfi type equation 220 225 233 Boussinesq equation 61 64Ч65 Branch points of a Riemann surface 3 8 10 11 16 41 56 59 65 70 71 74 76 80 84 106Ч108 110 111 113Ч115 143 179 Breather 40Ч51 283 Brownian motion 233 Bunimovich Ч Sinai theorem 219 220 233 BurgerТs Equation 28 136Ч140 157 160 161 329 330 C. Neumann problem 279 285 286 288 Cantor set 301 304 305 310 311 CauchyТs kernel 65 79Ч82 Caustic 23Ч24 34Ч35 240Ч243 279 Central limit theorem 233 Chaos / chaotic 40 105 331 336 339 342 Characteristic speed/velocity 4 5 14 15 64 Christophel symbols 144 Chromatography 144 145 153 Compatibility conditions in shock dynamics 357Ч359 Complex structure, deformation of 70 73 77 78 Complex tori 75 Configuration space 205 Conformal field theory 70 Connection 77 274 283 Conoidal waves 203 255 Conservation laws 5ff 37 68 90 94 145 146 149Ч153 236 240 330 331 332 345 357 360 Contact discontinuity 329 333 336 341 342 345 Contraction principle 351 Contravariant derivative 290 Convection 315 316 Couette flow 315 316 Covariant derivative 290 Critical magnetic field 183Ч201 Curvature 144 Cusp / cuspidal 119 126 133 139Ч140 Cuts 62Ч64 CYCLE 42Ч43 71Ч72 75 106 108 216 282 Darboux transformations 117Ч134 Defocusing NLS equation 21Ч27 235Ч238 242Ч245 248 249 251 276 279 283 Degree of mapping Z 1 Diffusion coefficient 219 220 226 228 233 234 Diffusion equation 219 226 228 Dirac operator 246 Dispersionless Lax equations 61Ч66 Dispersionless limit of integrable systems 165Ч174 Dispersive hydrodynamics 89Ч104 Divisor 120 122 125 177 179 297 302 304 Doppler frequency 324 325 Dressing 174 177 Driver amplitude 44Ч45 Driver frequency 43 Dubrovin equations 107 114Ч115 Duhamel integral 212 Dyson formula 260 Egorov class 145Ч147 Eikonal equation 22 28 34 35 36 240 241 Einstein Ч Kubo formula 233Ч234 Electrophoresis 144 145 153 Ellipsoid 276 277 Elliptic curve 120 122 Elliptic functions 68 265 Elliptic integrals 68 74 94Ч96 103 135 137 143 160 204 265 267 269 Energy density 316 Energy-phase modulation equations 43Ч44 Entropy solution of Hopf equation 333 Euler hydrodynamics equations 94 Euler system 237 238 254 Euler Ч Poisson type equation 90 96 136Ч139 Evolution equations 37 111 Finite horizon property of a billiard 222Ч223 228 230 233Ч234 Finite-gap 69Ч70 78Ч80 82Ч84 175Ч180 204 205 208 209 211 215 216 289 FlaschkaТs form of Toda lattice equations 6 Focusing NLS equation 27Ч37 235 236 242Ч245 249 283 Fractional power 62 Free energy 316 319 fundamental frequency 300 304 Galilean invariance of NLS 28 Galilei transformations 145Ч147 149 151 153 Gas dynamics 22 169 173 Gas law 22 23 Gauge invariance / gauge transform 168 172 Gauss hypergeometric function 100 Gelfand Ч Dikii Уfractional powerФ ansatz 62 Gelfand Ч Levitan integral equations 177 Generalized hodograph method 89 90Ч94 99 109 154 Genus 2 4 5 8 13 16 17 70 71 75 81 106 118 175 254 267 269 Geodesic flow, ergodic property of 219 Geometric phases 273Ч295 GHM see Generalized hodograph method Goursat problem 90 97 101 GP problem see Gurevich Ч Pitaevsky problem Grassmanian 118Ч120 GreenТs formula 231 GreenТs function 304 Gurevich Ч Pitaevsky problem 89 90Ч94 96Ч99 203 Hamilton Ч Jacobi equation 63 65 173 174 213 Hamiltonian 61Ч62 105Ч107 112 173 174 183 275Ч280 286 287 289 290 298 299 305 Hamiltonian flow 105 114 276 278 279 285 286 287 Hamiltonian system 68 105 107 143Ч146 150Ч153 167 173 216 236 257 273 278 280 281 285Ч288 298 302 harmonic oscillator 299Ч300 Heat transfer 316 Helix 320 326 Hilbert space 303 Hilbert transform 254 350 Hilbert Ч Schmidt operator 230 Hodograph 4 16 61 63 68Ч69 89 90Ч94 99 102 103 109 136Ч140 154 Holomorphic differential 42 72 73 75 77 106 177 Homoclinic 40 273Ч275 279 285Ч288 Hopf equation 249 329 331 333Ч337 341Ч344 359 Hydrodynamic symmetries 92 149 Hydrodynamic-type equations/systems 53 67 68 89 143 145 149Ч154 225 Hyperelliptic 70Ч78 80 106 126 175 204 209 211 215 276 Hypergeometric equation 99 Hypergeometric function 100 Integrable / nonintegrable numerical scheme 329 331 336 341 342 345 Integrable system 165Ч174 Invariant tori 105 216 276 279 300 302 Inverse scattering problem method 53Ч59 61 135 167 170 176 178 246 248 251 259 348 Inverse scattering transform 67 69 79 81 249 Ising chain 183Ч201 Isospectral symmetries 79Ч82 ISP method see Inverse scattering problem method Its Ч Matveev formula 175 204 Jacobi 204 Jacobi identity 144 Jacobi problem 286 288 Jacobi transformation 267 Jacobi variety 273 274 279 281 283 286 289 Jacobian 106 Jacobian matrix 332 Jost functions 54 Kac Ч van Moerbeke lattice 331 341 342 Kadomtsev Ч Petviashvili equation 67 69 78Ч84 123 132 167Ч168 Kadomtsev Ч Petviashvili equation, dispersionless 167Ч168 Kadomtsev Ч Petviashvili equation, finite-gap inverse scattering transform for 81 Kadomtsev Ч Petviashvili equation, finite-gap solutions 69 78Ч79 82Ч84 Kadomtsev Ч Petviashvili equation, isospectral symmetries 79Ч82 Kadomtsev Ч Petviashvili equation, Lax pair for 81 Kadomtsev Ч Petviashvili equation, nonisospectral symmetries 82Ч84 KAM theory see Kolmogorov Ч Arnold Ч Moser theory KdV equation, see Korteveg Ч de-Vries equation KdV functions 212 KdV hierarchy 84 347Ч356 KdV hydrodynamics 89 91 KdV Ч Whitham problem 2 3 KdV Ч Whitham problem vs. Toda Ч Whitham problem 2 kinetic energy 305 306 310 KN equation see Krichever Ч Novikov equation Kolmogorov Ч Arnold Ч Moser theory 114 180 205 302 Kolmogorov Ч Petrovsky Ч Piskunov problem 322 Korteveg Ч de-Vries equation 2 4 53Ч55 61 64 67Ч88 89 90Ч93 95 96 119 126Ч128 131Ч133 143Ч155 157 162 163 175Ч181 203 205Ч209 216 238 248 249 259 275Ч280 284Ч291 298 330 345 347-356 Korteveg Ч de-Vries equation, 79 Korteveg Ч de-Vries equation, 53 55 Korteveg Ч de-Vries equation, averaged 4 68 70 143Ч155 Korteveg Ч de-Vries equation, dispersionless 4 53Ч55 61 64 180 Korteveg Ч de-Vries equation, finite-gap solutions 69 79Ч80 82Ч84 175Ч180 208 209 216 Korteveg Ч de-Vries equation, isospectral symmetries 79Ч82 Korteveg Ч de-Vries equation, Lax pair for 79 Korteveg Ч de-Vries equation, linearized 206 Korteveg Ч de-Vries equation, moving waves 67 Korteveg Ч de-Vries equation, nonisospectral symmetries of 67Ч88 Korteveg Ч de-Vries equation, quasi-periodic solutions 4 Korteveg Ч de-Vries equation, reflecting coefficient for 54 Korteveg Ч de-Vries equation, shock problem for 176Ч179 Korteveg Ч de-Vries equation, symmetries of 69 Korteveg Ч de-Vries equation, Tsarev equations for 90 162 Korteveg Ч de-Vries equation, wave breaking problem for 89 90Ч93 Korteveg Ч de-Vries equation, weak dispersion limit of 2 4 kp see Kadomtsev Ч Petviashvili equation KP flow 117 118 125 KP hierarchy 119 KP vertex operator 130 Krasnoselskii theorem 306 Krichever Ч Novikov equation 119 127 131Ч133 Krichever Ч NovikovТs formalism 120 123 KricheverТs scheme 109 Kruskal symmetries 149 150 152 Kuzmak Ч Whitham averaging ansatz 105 114 Lagrangian 173 Lagrangian submanifold 278 280 281 286 289 Laminar state 315 316 Laplace integral 261 Laplace Ч Beltrami type operator 290 Lax entropy 237 Lax equations 61Ч66 167 Lax equivalence theorem 227 233 Lax pairr 6 79 81 257 Lax Ч Levermore minimizer 157Ч164 Lax Ч Levermore problem 203 Lax Ч Levermore Ч Venakides theory 14 135 162 Legendre transform 305 Lie algebras 289 Lie derivative 77 Line bundle 118 120Ч122 126 Linear fractional transformation 123 127 Linear stability 318Ч319 Liouville equation 233Ч234 Liouville theorem 186 Liouville tori 105Ч116 Lorentz gas of hard spheres 219Ч227 229Ч230 Lorentz gas with accomodation reflection 221Ч223 227Ч228 230-233 Lyapounov functional 316 Lyapounov theorem 316 Lyapounov Ч Schmidt decomposition 302 304Ч305 Magnetic field 183Ч201 Markov partition 219 233 Maslov method 289 Modulation equations 27Ч28 37 39Ч52 89 331 333 342 345 Moduli space 76 78 273 monodromy 273Ч295 Moving frame 258 Multi-phase averaged system 135 143 149 Multifrequency averaging theory 203Ч217 Multiphase asymptotics 204 215 Nash Ч Moser method 297 302 304 Neumann system 105 111 112 114 NLS equation see non-linear Schr Non-linear Schr 21Ч38 55 61 93Ч95 169 180 235Ч255 276 279Ч281 283 291 298 328 Non-linear Schr 21Ч27 89 93Ч94 235Ч238 242Ч245 248 249 251 276 279 283 Non-linear Schr 27Ч37 235 236 242Ч245 249 283 Non-linear Schr 28 Non-linear Schr 21Ч37 235Ч255 Non-linear waves 297Ч313 Nondissipative shock waves 89Ч92 97 98 99 102 Nonisospectral integrable equations 69 Nonisospectral symmetries 78Ч79 82Ч87 Nonlinear wave equation 299 303 305 NSW see Nondissipative shock waves Number density 220Ч221 223Ч225 228 233 Numerical scheme 329 342 Optical fibers 24Ч27 Optical pulses 24 Optical shocks 21Ч37 Oscillations arising in numerical experiments 329Ч346 Painleve equation 105 Parabolic structure 121 122 Pauli matrices 183 Period matrix 41Ч43 78 Period-two oscillations 331Ч333 336Ч345 Periodic solutions 297 299 300Ч302 304 307 310 Perturbed modulation equations, numerical integration of 44Ч51 Phase space 220 276 279 280 297 302 Poisson bracket 62 144 174 236 247 Potential 80 81 90 94Ч96 105 107 112 150 177 179 211 235 236 240 299 305Ч307 311 Potential metric 146 151Ч153 Pre-chaotic 40 52 Presoliton solutions 291 Principle of least action 305Ч306 311 312 Quadric 274 276 288 Quasi-periodic geodesic 277 279 Quasi-periodic solutions 286 291 297 Quasi-simple wave 89 90 92 99Ч103 367 Quasiclassical limit 53Ч59 207 Quasimomentum 72 80 211 Reflection laws 219Ч222 234 Regularization of integrals 53 57 Resonance 105 203Ч217 297Ч313 Resonant group 300Ч302 304 Reynolds number 315 RH problem see Riemann Ч Hilbert problem Riccati equation 54 124 Riemann (diagonal, characteristic) form 68 84 89 254 Riemann bilinear relations 72Ч74 268 Riemann constants 78 81 Riemann invariant form of 61 Riemann invariants 22 62 68Ч70 92 143 238 239 249 255 Riemann manifold 290 Riemann metric 290 Riemann problem 75Ч78 Riemann surface 3 8 10 11 16 41Ч43 56 59 65 70Ч78 80 81 112 143 146 216 254 269 274 276 280 282Ч284 286 287 289 Riemann surface, branch points of 3 8 10 11 16 41 56 59 65 70 71 74 76 80 106Ч108 110 111 143 Riemann surface, cycles on 42Ч43 71Ч72 106 108 282 Riemann surface, deformations of 75Ч78 Riemann surface, differentials on 71Ч75 106 Riemann surface, genus of 70 71 75 81 106 254 269 Riemann surface, local parameter 71 Riemann surface, matrix of periods 78 Riemann surface, moduli space of 75Ч78 Riemann theta function 41 78 106 112 113 118 204 211 Riemann wave 92 99
–еклама
 |
|
ќ проекте
|
|
ќ проекте



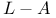 pair
pair 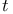 -function
-function 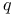 -function
-function 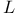 -equation for
-equation for  dinger equation
dinger equation