|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hadley G. — Linear programming |
|
|
 |
| Предметный указатель |
Abadic, J. 420
Activity vector 76 450 481
Addition, of matrices 25
Addition, of matrices, of vectors 37
Adjoint 33
Aggregation problem 493
Allen, R. G. D. 104
Alternative activities 501
Alternative optima 99
And extreme points 100
Artificial variables 118
Artificial vectors 118
Back-substitution 51
Basic solutions 54
Basic variables 54 85
Basis 43
Basis matrix 84
Beale, E. M. L. 190 196 266
Berge, C. 373
Birkhoff, G. 67
Blending problems 458
Boles, J. N. 463
Bowman, E. H. 463
Branch 286 331
Capacitated transportation problem 395
Case study 433
Caterer problem 465
Charnes, A. 20 104 120 175 196 293 322 463 472
Closed Leontief model 499
Cofactor 31
Column vector 37
Complementary slackness 239
Components of a vector 37
Cone 65
Cone, convex 65
Cone, polyhedral 65
Connected graph 333
Constraint 4 6
Convex combination 58 61 99
Convex polyhedron 61
Convex set 18 58 61
Convex set, extreme point of 18 59 100
Cooper, W. W. 20 104 196 293 322 463 472
Cut in a network 349
Cut in a network, capacity of 349
Cycling 113 174
Cycling, example 190
Cycling, prevention of 181 185
Dantzig, G. B. 19 20 149 175 183 196 197 218 258 266 293 318 322 373 398 400 417 420 463 502 508
Decomposable Leontief systems 495
Decomposition principle 400
Degeneracy 54 81 113
Degeneracy, examples 187
Degeneracy, in transportation problems 299
Degeneracy, resolution of 174
Dennis, J. B. 322
Dependence, linear 40
Determinant 30
Diet problem 462
Dorfman, R. 508
Dual electrical networks 226
Dual linear programming problems 222
Dual linear programming problems, economic interpretation 483
Dual simplex algorithm 242
Dual simplex algorithm, example of 253
Dual simplex algorithm, geometric interpretation 255
Dual simplex algorithm, initial solution 252
Dynamic Leontief models 504
Edge of a convex set 65 165
Edge of a network 331
Eisemann, K 318 322 463
Euclidean space 40
Extended requirements space 161
Extreme points 59 100
feasible 77 80
Feasible solution 6 71 80
Ferguson, A. R. 318 322
Flood, M. M. 322 431 463
Flows in networks 334
Flows in networks, definition of 335
Flows in networks, max flow-min cut theorem 351
Flows in networks, maximal 335
Flows in networks, steady state 335
Ford, L. R., Jr 258 266 340 351 368 373 374 395 420
Fulkerson, D. R. 258 266 340 351 368 373 374 395 420 463
Gainen, L. 464
Gale, D. 20 374 417 420
Gasoline blending 458
Gass, S. I. 104 118 420
Gaussian reduction 51
Generalized linear programming problems 183
Generalized transportation problems 314
Generalized transportation problems, example 315
Geometric interpretation of the simplex method 19 158 162
Georgescu — Roegen, N. 506
Goldman, A. J. 266
Graph 331
Guillemin, E. A. 266 374
Gunther, P. 463
Hadley, G. 67
Half-line 65
Half-space 58
Half-space, closed 58
Half-space, extreme supporting 66
Half-space, open 58
Henderson, A. 104 196 463
Hitchcock, F. L. 21
Hoffman, A. J. 190 196
Honig, D. P. 464
Houthakker, H. S. 323
Hyperplane 58
Hyperplane, extreme supporting 66
Hyperplane, supporting 62
Identity matrix 26
Inconsistency 121
Independence 40
Industrial applications 429
Initial solution 116 181 184
Input-output analysis 487
Integrality property for transportation problems 280
Interindustry models 227 487
Intersection 56
Inverse matrix 34
Inverse matrix, computation of by partitioning 35
Inverse matrix, power series 36
Inverse matrix, product form 48
Jacobs, W. W. 465
Johnson, S. 444 464
Kantorovitch, L. 20 21
Karlin, S. 104
Kemeny, J. G. 67
Konig, D. 374
Koopmans, T. C. 20 21 67 104 323 493 508
Kuhn, H. W. 20 368 374 417 420
Lagrange multipliers 18
Lemke, C. E. 243 266
Leontief, W. 20 22 227 487
Lexicographically ordered vectors 183
Line 57
linear combination 40
Linear dependence 40
Linear equations 50
Linear forms 5
Linear inequalities 4
Linear programming problems 4 71 76 175 183
Linear transformation 55
Loop 287 332
Loop, directed 287
Loop, simple 288
Lower bounds 394
| Machine-assignment problems 437
MacKenzie, H. C. 464
MacLane, S. A. 67
Manne, A. S. 420 458 464
Matrices 24
Matrices, addition 25
Matrices, adjoint 33
Matrices, diagonal 27
Matrices, element 24
Matrices, identity 26
Matrices, inverse 34
Matrices, multiplication 25
Matrices, null 27
Matrices, skew-symmetric 28
Matrices, symmetric 28
Matrices, transposed 27
Matrix solution 344
Max Flow-Min Cut Theorem 351
Maximal flow in a network 334
Maximal flow in a network, examples 337 346
Maximal flow in a network, intuitive approach 334
Maximal flow in a network, labeling technique 340
Maximal flow in a network, proofs 349
Mellon, B. 463
Minimax theorem 415
Minor 32
Mirkil, H. 67
Morgenstern 0 417 508
Network 334
Node 331
Non-negative variables 5 71
Non-negativity restrictions 6 71
Nondcgenerate 54
Nondegenerate basic feasible solution 81 176
Nonsingular matrix 34
Null matrix 27
Objective function 6 76
Optimal basic feasible solution 97
Optimal product mix 447
Optimality criterion 95 97
Orchard — Hays, W. 197 218 266 420
Orden, A. 125 149 183 196 218 266 373 374
Orthant, non-negative 60
Parametric programming 380
Parametric programming, example 386
Parametric programming, of price vector 380
Parametric programming, of requirements vector 382
Partitioning of matrices 28
Path 285 332
Path, simple 288
Pauli, A. E. 464
Personnel-assignment problems 367
Perturbed problem 175
Petroleum-refinery operations 452
Phase I 150 205
Phase II 151 206
Polyhedron, convex 61 158
Postoptimality problems 379
Primal problem 223
Primal-dual algorithm 257
Primal-dual algorithm, example of 263
Primal-dual algorithm, for transportation problems 351
Product form of inverse 48 217
Production scheduling 439
Programming problems 1
Rank 47
Redundancy 121 153
Regular-time, overtime production 439
Reinfeld, N. V. 323
Requirements space 158
Revised simplex method 197
Revised simplex method, example 211
Revised simplex method, Standard Form I 201
Revised simplex method, Standard Form II 205
Revised simplex method, tableau for 204
Row vector 37
S simplex method, change of basis in 87 109
S surplus variable 72
S Tornheim, L. 67
Saaty, T. L. 420
Saddle point 413
Samuelson, P. A. 508
Scalar product 39
Schlaifer, R. 463
Secondary constraints 398
Set 55
Set, convex 58
Set, point 55
Shapley, L. S. 417
Simonnard, M. A. 323
Simplex method 17 71 10
Simplex method, examples of 134
Simplex method, initial solution for 116
Simplex method, summary of 132
Simplex method, tableau for 124
Simplex method, vector to enter basis 111
Simplex method, vector to leave basis 113
Sink 334
Skew-symmetric matrix 28
Slack variable 72
Snell, J. L. 67
Snow, R. N. 417
Solow, R. 508
Solutions space 162
Source 334
Spanning set 43
Square matrix 25
Stanley, E. D. 464
Stigler, G. J. 22 463
Strategy 412
Strategy, mixed 414
Strategy, pure 414
subspace 47
Sum check 14
Symmetric game 419
Symmetric matrix 28
Symonds, G. H. 464
Tanker routing problems 431 472
Theory of the firm 476 481
Thompson, G. L. 67
Thrall, R. M. 67
Ties, breaking of 112 113 181 185 18
Transformation formulas 114
Transhipment problem 368
Transportation problem 7 273
Transportation problem, 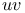 -method for 309 -method for 309
Transportation problem, capacitated 395
Transportation problem, initial solutions to 304
Transportation problem, integral solutions to 280
Transportation problem, primal-dual algorithm for 351
Transportation problem, resolution of degeneracy in 299
Transportation problem, stepping-stone method for 291
Transportation problem, tableaux for 284
TRANSPOSE 27
TREE 289 333
Tucker, A. W. 266 417 420
Two-phase method 149
Unbounded solutions 14 93
Unimodular property 277
union 56
Unit vectors 38
Unrestricted variables 168
Upper bounds 387
Upper bounds, on transportation problems 395
Vajda, S. 104 464
Value of a game 415
Variables 4 5 71
Variables, artificial 118
Variables, basic 85
Variables, dual 223
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



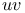 -method for
-method for