This dissertation is concerned with the numerical investigation of particle-laden flows. The simulations are based on a pseudo-spectral method to solve the fluid equations combined with a Lagrangian point-particle model for the particulate phase (Eulerian-Lagrangian approach). Two flow configurations of increasing complexity are studied with the aim of unraveling some fundamental properties of particle settling in disperse two-phase flows.
The first configuration is a suspension drop (initially spherical swarm of particles) settling in a fluid under the influence of gravity. The focus is on a range of moderate drop Reynolds numbers
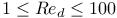
where the suspension drop deforms into a torus that eventually becomes unstable and breaks up into a number of secondary blobs. The flow remains laminar, which allows for a systematic variation of several parameters. The influence of the Reynolds number, the number of particles inside the drop, the initial particle positions and some numerical quantities are studied in detail.
The second configuration is an initially random suspension of particles in homogeneous turbulence. Here, the focus is on the enhancement of the mean particle settling velocity in a turbulent carrier fluid compared to the settling velocity of a single particle in still fluid. Results are presented for both one-way coupling (the fluid flow is not affected by the presence of the particles) and two-way coupling (the particles exert a feedback force on the fluid). The mechanism responsible for an additional increase in settling velocity in the case of two-way coupling is analyzed. Moreover, a careful comparison with recent experimental results is performed for a microscale Reynolds number
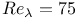
of the turbulent carrier fluid.
 |
|
О проекте
|
|
О проекте


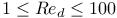 where the suspension drop deforms into a torus that eventually becomes unstable and breaks up into a number of secondary blobs. The flow remains laminar, which allows for a systematic variation of several parameters. The influence of the Reynolds number, the number of particles inside the drop, the initial particle positions and some numerical quantities are studied in detail.
where the suspension drop deforms into a torus that eventually becomes unstable and breaks up into a number of secondary blobs. The flow remains laminar, which allows for a systematic variation of several parameters. The influence of the Reynolds number, the number of particles inside the drop, the initial particle positions and some numerical quantities are studied in detail.
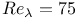 of the turbulent carrier fluid.
of the turbulent carrier fluid.